气固两相湍流场纳米颗粒演变特性综述

石瑞芳，林建忠

浙江大学 航空航天学院 流体工程研究所，杭州 310027

存在于流动气体介质中的纳米颗粒以气溶胶的形式出现，多数情况下流动呈湍流状态，如空气净化系统、喷射器、呼吸道流[1]、汽车尾气喷流、地效飞机悬停流场[2]和燃烧排气系统等。纳米颗粒两相湍流在自然界和实际应用中很普遍，了解湍流场内纳米颗粒的尺度分布和演化机理，有助于人们在实际应用中对其控制从而达到预期的目标。

要有效地预测和控制纳米颗粒在湍流场中的分布，就要了解颗粒在湍流场中的生成、对流、扩散、凝并、破碎等机理，为此人们进行了大量的研究[3-8]。对单颗粒而言，由于Stokes数(St)远小于1，所以当颗粒的体积分数较小时，可以忽略颗粒对流场的影响而采取单向耦合的方法求解方程。但如果颗粒呈致密的类分形团块，因颗粒具有独特的传热传质特性，故需考虑颗粒对流场的影响[9]。纳米颗粒两相湍流的湍动特性体现在流场速度脉动、颗粒数密度脉动、化学组分浓度脉动、温度和饱和度脉动等[10]。与层流相比，湍流场对颗粒扩散的影响更大并显著增强颗粒在流场中的混合。受湍流场影响，颗粒的分布高度不均匀[11-13]，湍流会在流动界面卷起形成兼具大尺度和小尺度运动的拟序结构，该结构的存在对增强颗粒凝并和弥散起着重要的作用[5]。由于纳米颗粒两相流的颗粒数一般都非常多，所以对颗粒群的研究通常采用统计的方法。常见的研究纳米颗粒动力学的方法有分子动力学、分区法、矩方法、蒙特卡洛方法等[14]。

以下从纳米颗粒气固两相湍流场中最常见的颗粒生成、凝并、破碎和沉降4个方面叙述相关的研究状况和进展。

1 颗粒生成

不同尺寸和结构的颗粒，呈现的物理性质往往有所差别。实际工业应用中，通过不同方式制备特定尺度范围的功能性纳米颗粒。图1给出了纳米颗粒的生成方式，由于本文涉及的是气固两相流，所以以下主要介绍与此相关的流场中颗粒的成核和表面反应生长(冷凝)过程。

图1 纳米颗粒的产生方式

1.1 纳米颗粒在不同环境中的生成机理

纳米颗粒可以在大气环境[15-16]、湍流喷雾火焰[17]和湍流反应流[18]等不同环境下生成。颗粒在气体环境中的生成是气相化学反应产生的可冷凝蒸汽物质因表面冷却、绝热膨胀或混合、湍流混合[19]或化学过程产生的过饱和所导致；而在液相中的生成与颗粒的粒径、化学成分、表面和电荷性质等有关[20]。不同来源与生成机理的颗粒呈现出不同的颗粒尺度、形态和结构特性及散射性、吸附性和生长性等物理特性。

液相体系中得到纳米颗粒如水/有机溶剂在聚合物做保护剂的前提下被还原剂还原生成金属纳米微粒，其形状主要取决于保护剂的种类、剂量、聚合度及配料的速率和顺序等，产物有纳米线、棒、无规则、球、椭球或三角形等多种形式。太阳能系统加入不同形状的银纳米颗粒可不同幅度提高溶液的吸光度和光热转换性[21]。航天复合材料，加入纳米颗粒可降低航天器材料的质量损失和剥蚀率[22]，激光加工制备的纳米尺度颗粒和微孔阵列形成微观机械咬合等可提高接头的强度和黏附性[23]。

相对而言，气相体系下制备的纳米颗粒不发生化学反应，仅通过热源使可凝性物质在高温下蒸发，并在惰性气体氛围下冷凝从而形成纳米颗粒。颗粒大小取决于惰性气体压力和温度，可制备精细表面清洁的颗粒，但效率低难控制产物形状。产物形状更多是颗粒或链状连接颗粒乃至纳米线。一维的纳米线，应用于传感器原件，表现出极高的柔韧性、响应速度和灵敏度[24]。另一种气体原料在气相介质内发生化学反应得到基本粒子则会经成核、生长阶段，更多以团聚体或点、角相接的团簇或小颗粒在大颗粒上附着的低维附聚体形式存在。源自气相燃烧合成的颗粒，其颗粒除离散单体形式外，更多的是颗粒聚集形态，如原级粒子以面相接，难再分散的凝聚体。悬浮纳米颗粒在界面堆积可改变沸点提高液体燃料着火率[25]。

颗粒在生成阶段影响其尺度和形状的主要控制参数是成核和生长速率。成核需要克服能垒形成的临界核才能实现，成核过程中所需的成核能量决定了成核速率，随着能垒的增加，成核速率呈指数下降[26]。颗粒成核和表面生长理论如表1[27-32]所示，颗粒成核方程为

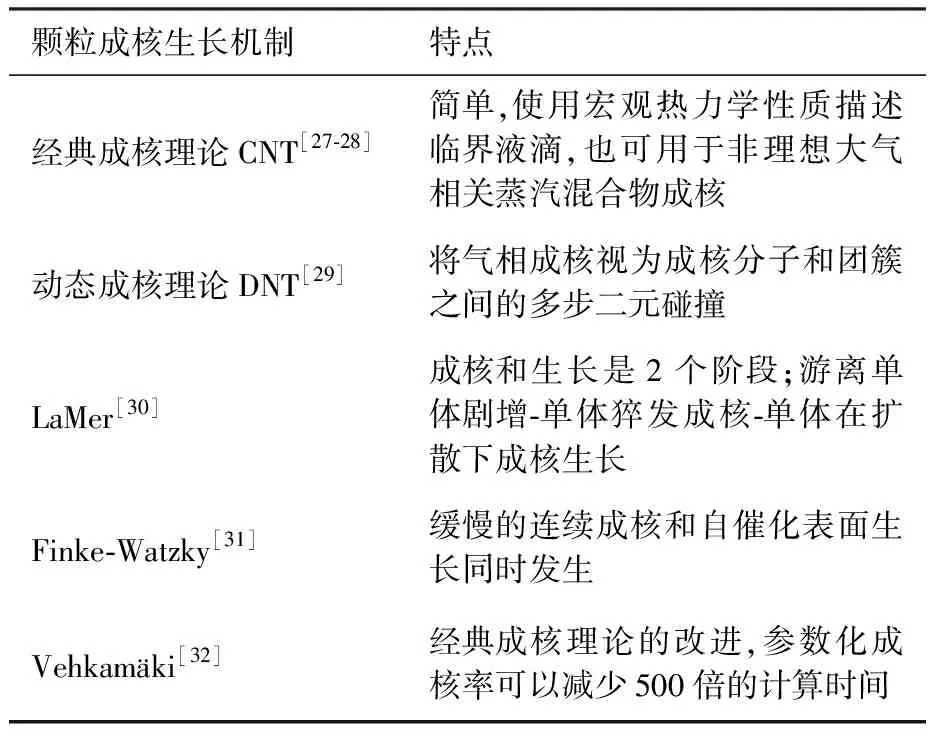
表1 颗粒成核和生长理论

(1)

式中：n(v,t)表示以颗粒体积v和时间t为变量的颗粒尺度分布函数；v*为生成的稳定单体体积；δ为狄拉克函数；G(v)和J表示冷凝导致的颗粒生长核函数与成核速率。

1.2 颗粒生成的数值模拟

发动机尾气排放是典型的颗粒生成过程，人们对与尾气排放相关的各类射流以及与扩散火焰反应器相关的颗粒生成机理进行了一系列研究。Yin等用大涡模拟方法结合颗粒成核和演化模型先后研究了运动排气双喷流[33]和撞击双射流[34]中纳米颗粒的形成。受行驶物尾部流场结构的影响，颗粒的生成取决于环境风速与排气速度之比，较高的环境风速会降低纳米颗粒的生成速率并增大颗粒的尺度。在撞击射流中，颗粒的成核主要发生在射流界面及撞击平面附近的区域，其中撞击平面附近颗粒成核数最多；喷嘴到撞击平面的距离越大越不利于颗粒成核。在平行双射流中，颗粒成核区与撞击射流的情形类似，硫含量、相对湿度、射流雷诺数能促进颗粒成核[35]。Yu等[36]数值模拟了扩散火焰反应器四异丙醇钛分解均相成核和颗粒的形成过程。在此基础上，Yu等[37]进一步给出了前驱物量值对扩散火焰反应器合成非球形二氧化钛纳米颗粒的影响。此后，Yu等[38]将大涡模拟方法与新提出的泰勒级数展开矩方法结合，对发动机尾气中的颗粒生成进行了数值模拟，发现大涡主导着颗粒的演化，硫化物-水二元均质成核主要出现在排气与周围冷气体的交界面；燃料含硫量和相对湿度的增加或环境温度的降低均导致颗粒生成率以及平均粒径的增加；随着湍流度的增大，颗粒的分布变宽、平均直径变小(见图2)[38]。

图2 湍流强度I对颗粒数密度和平均粒径的影响[38]

Yu和Lin[39]研究了有和无背景颗粒情况下水-硫化物的混合物在大气环境中二元均相成核的过程，发现颗粒成核及其后续的运动强烈依赖于硫化物的浓度。Lin和Liu[40]对混合层中颗粒成核的研究表明，温度较低的区域颗粒更容易成核。Chan等[41]对飞行器近尾迹区颗粒的凝并、成核和湍流弥散过程的研究发现，颗粒凝并的时间尺度较大，而成核的时间尺度较小。Chan等[42]将双峰泰勒级数展开矩方法与大涡模拟方法结合，证实了湍流的拟序结构增强了颗粒的扩散。Garrick[18]研究了二氧化钛颗粒生成过程中冷凝和凝并所起的作用，如图3[18]所示，在近射流区，成核和冷凝起主导作用，一旦射流核心区坍塌，凝并起主导作用。图中1 nm颗粒(绿色)遍布整个流场，而凝并后的3 nm颗粒仅存在于下游区域。

图3 颗粒在流场中的瞬时分布[18]

2 颗粒凝并

颗粒凝并是颗粒相互碰撞并黏附形成大颗粒的过程，如表2[43]所示，导致颗粒碰撞的原因包括布朗运动、湍流场剪切作用、速度梯度、差异沉降等。颗粒的凝并取决于颗粒的尺度和流场的特性[44-45]。

表2 颗粒凝并机制[43]

2.1 布朗凝并

布朗凝并通常发生在小于1 μm的颗粒，不同角度、不同直径和不同碰撞类型的颗粒发生碰撞时，其碰撞凝并有不同的表达形式[46-50]。Smoluchowski最早提出凝并模型，将颗粒尺度谱的演化转化为颗粒碰撞频率函数的演化，后来Müller[51]发展了连续颗粒尺度分布的数密度方程：

(2)

式中：β(v,v1)表示体积分别为v1和v的两颗粒凝并的颗粒凝并核函数，取决于颗粒间的碰撞和凝并率。颗粒布朗凝并取决于颗粒布朗运动引起的碰撞，当颗粒粒径远大于气体分子平均自由程时，颗粒的碰撞受扩散制约；而当粒径远小于分子平均自由程时，颗粒的碰撞可由分子运动理论确定。在近连续区和自由分子区，颗粒的布朗凝并核函数可分别表示为[52]

(3)

(4)

式中：λ为气体分子平均自由程；K和T分别为Boltzmann常数与温度；μ和ρ为流体动力黏度和密度；vp和rp为初始颗粒的体积和半径;Df为颗粒分形维数，表征颗粒的形态。

2.2 湍流凝并

湍流凝并通常发生在粒径为1 μm以上的颗粒或者是高湍流情况下的亚微米颗粒。Camp和Stein[53]用湍动能耗散与流体黏度比值的平方根代替湍流中的速度梯度，将用于层流剪切凝并的表达式推广到湍流剪切凝并。粒径为1 μm以下的颗粒通常位于黏性区，Saffman和Turner[54]导出了黏性区内粒径远小于Kolmogorov尺度的颗粒凝聚核，其中由剪切引起的球形颗粒凝并核为

(5)

式中：ν和ε分别为流体黏度和湍动能耗散率；r1和r2为颗粒半径。Flesch等[55]将式(5)拓展到分形结构体：

(6)

总的颗粒凝并核可以由布朗凝并βB和湍流凝并βT构成：

(7)

在实际应用中，不同湍流场对颗粒凝并有不同的作用。冯鹏等[56]比较了不同类型的绕流场中颗粒的凝并，发现Y型绕流场由于有更强的涡度场，所以凝并最为明显。Yu等[57]研究了湍旋流中的颗粒凝并，分析了涡流发生器类型、结构参数和运行参数对亚微米颗粒凝并的影响，给出了当螺旋叶片内外径比为0.3时颗粒浓度和速度对100 nm颗粒凝并的影响(如图4[57]所示，N为颗粒浓度,U为流场速度，dp为颗粒直径，r为颗粒体积分数)，说明颗粒浓度呈单峰形式分布且峰值随着流速的增加而迅速增加。进一步的研究表明，如果流场的速度增加，则小颗粒的数量增加，而大颗粒的数量减少，其原因一是较高的流速会影响颗粒在浓度梯度方向上的运动，颗粒扩散受到一定程度的抑制，使得颗粒凝并削弱；原因二是较高流速使得颗粒停留在流场中的时间更短，颗粒碰撞的概率降低。若保持流速不变，分布曲线向右移动，表明颗粒凝并增强，因为较高的颗粒浓度导致颗粒之间更多的相互作用和碰撞。

图4 浓度和速度对凝并的影响[57]

2.3 数值求解方法

Yu等[58-61]提出了对颗粒数密度方程进行求解的泰勒级数展开矩方法并用于多种流场的计算，在保证精度的同时提高了计算效率。在此基础上，Lin和Chen[62]基于分区法的渐近解，改进了泰勒级数展开矩方法，使得当颗粒尺度分布接近自相似或凝并时间足够长时，能更精确地预测零阶和二阶矩的演化。Chen等[63]在泰勒级数展开矩方法的基础上，提出了直接展开矩方法并用于求解颗粒数密度方程，给出了较大颗粒尺度范围内颗粒布朗凝并的解[64]。Yu和Lin[65]提出了一种混合矩法来求解颗粒数密度方程，该方法采用三阶泰勒级数展开来逼近具有附加性形式的凝聚核，用拉格朗日插值来逼近隐式矩，从而避免了针对特定核的推导，其有效性在应用中得到了证实。

2.4 湍流场的影响

Garrick[66]在平面混合层中研究了湍流对颗粒凝并的影响，发现在有颗粒的区域，流场大尺度与亚网格尺度的相互作用能促进颗粒的凝并。Das和Garrick[67]对平面射流中二氧化钛颗粒凝并的研究表明，小尺度的波动对颗粒的凝并既有促进作用，也有抑制作用，但后者更为明显。纳米颗粒在充分发展的湍流管道内会向管道中心移动，单分散颗粒会因布朗运动的存在而凝并成不同大小的颗粒簇，在管道中心则产生最大的颗粒团[68]。Lin和Chen[69]发现，在充分发展的湍流边界层中，颗粒的凝并与扩散使得颗粒的粒径从壁面向外侧增加，颗粒在向外侧迁移中因较高的局部浓度而促进了凝并，导致较大的颗粒在外侧积聚。Lin和Liu[40]的研究表明，混合层中的纳米颗粒凝并受初始颗粒分布及湍流扩散控制，图5[40]给出了颗粒在不同流向位置的无量纲平均直径dave分布，可见在向下游发展过程中，颗粒的直径分布逐渐变宽。

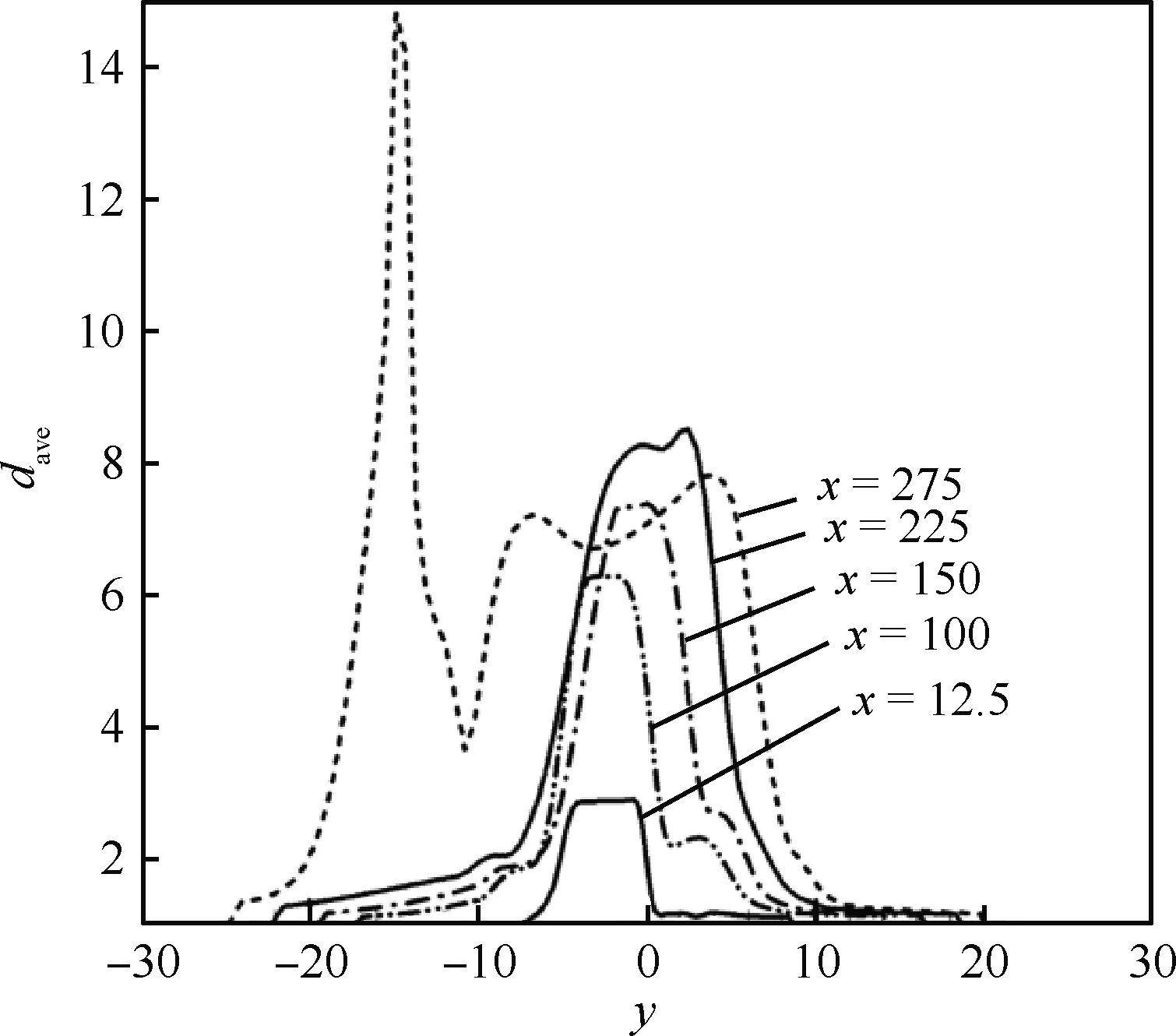
图5 颗粒在不同流向位置的平均直径分布[40]

湍流场对颗粒凝并的影响除了湍流强度的因素外，还体现在由湍流脉动所引发的颗粒数密度脉动。Lin等[70]以湍动能与平均动能的比值来表征颗粒数密度脉动对颗粒凝并的影响，并通过圆管湍流场的计算验证了其有效性，数值模拟结果表明，在小Schmidt 数和高Reynolds数情况下，颗粒呈现出更大的平均直径和更强的尺度分散性。然而，当流场存在回流区或湍动能远大于平均动能时，以上方法不适用，对此Yang等[71]在以上方法基础上提出了另一种形式，即以湍动能与总动能的比值来表征颗粒数密度脉动对颗粒凝并的影响。Shi等[72]采用这一方法对通风室内非球形颗粒的凝并进行了数值模拟，得到了与实验[73]比较吻合的结果。在有颗粒凝并的流场中通常伴随着颗粒破碎，Gan等[74]数值模拟了平面湍射流中存在颗粒凝并和破碎情况下的颗粒数密度方程，发现存在凝并与破碎的动态平衡。Barthelmes等[75]从理论上研究了非球形颗粒的动力学行为，建立了剪切诱导的颗粒凝并和破碎的群体平衡模型。

3 颗粒破碎

颗粒凝并后形成尺度较大的团聚体容易在流场剪切和其他因素作用下发生解体破碎，与颗粒破碎相关的方程为

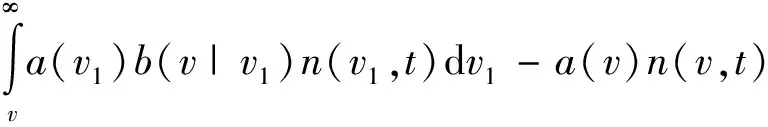
(8)

式中：a(v)为破碎核函数，表示体积为v的颗粒的破碎频率，有指数和幂律等形式；b(v|v1)为碎片分布函数，表3给出了常见碎片的分布形式。Marchisio等[76]在考虑不同破碎核与子分布形式下，用积分矩方法模拟了颗粒的凝并和破碎，并给出了存在凝并和破碎时的渐近解[77]。

表3 颗粒破碎后的碎片分布

在搅拌流场中，颗粒容易受搅拌的外力场作用而破碎[78]，搅拌器的速度和流动速度是影响颗粒破碎的2个主要因素。Pandya和Spielman[79]根据颗粒破碎和侵蚀机制，提出了一个控制湍流中颗粒团聚体粒径分布的平衡方程式。此后，Hill和Ng[80]用新的离散化方法，推导出了适用于分散体系颗粒群的破碎方程，解决了区间交互问题，明显提高了对颗粒粒径分布的预测精度。

剪切破碎是导致颗粒破碎的主要因素，由剪切导致的有效破碎系数取决于剪切率和颗粒的体积分数，体积分数越大，颗粒的碰撞次数增加，剪切率越高意味着碰撞能量越强，颗粒越容易破碎[81]。当剪切率一定时，颗粒的体积分数增加，稳态的颗粒尺度减小。

当流场进出口的差压较大时也容易导致颗粒破碎。Yuan等[82]研究了颗粒从高压容器的喷嘴中排出的情形，通过控制压力使得颗粒破碎后的尺度满足所需的要求。Badyga等[83]对转-定子混合器和高压喷嘴粉碎机流场的数值模拟结果表明，高压喷嘴粉碎机对颗粒的破碎产生更明显的效果。图6[83]给出了压差(Δp)对颗粒平均粒径(L30)的影响，可见进出口的压差越大，颗粒的破碎程度越高。

图6 压差对平均粒径的影响[83]

4 颗粒沉降

在气体净化设备、气溶胶测量仪器以及人体呼吸这样的纳米颗粒气力输送过程中，预测颗粒的沉降速率至关重要。颗粒的沉降取决于颗粒的尺度、形状和流体性质等因素。导致颗粒沉降的因素有重力、扩散、惯性撞击、电场和热迁移等[19]。在湍流场中，颗粒的沉降与黏性底层和过渡层中的参数密切相关，在充分发展的湍流边界层中，粒径较小颗粒的沉降主要因布朗扩散和湍流扩散所致；粒径较大的颗粒主要受其惯性和重力支配，当地流场的影响较小。

颗粒沉降到壁面上会导致在壁面上的沉积，沉积率或输运颗粒损失率η可表示为

(9)

式中:Ci和Co为进出口颗粒的质量浓度或数密度；fp为颗粒流过管道的通过率，对充分发展的圆管湍流场有：

(10)

其中：颗粒的沉降速度vd定义为单位时间、单位面积上的颗粒通量Jd和截面平均浓度Cave的比值；l和D分别为管道长度和直径；U为流场速度。用壁速度uw无量纲化，可得无量纲沉降速度：

(11)

Lai和Nazaroff[84]考虑了布朗扩散和湍流扩散及重力因素对颗粒沉降的影响，提出了新的半经验沉积模型(也称“三层模型”)用于预测沉降到光滑表面的颗粒：

(12)

式中：εp为颗粒的涡流扩散率；DB为颗粒在边界层内的布朗扩散系数；vs为重力引起的沉降速度；i表示曲面方向(表面向上取1，向下取-1，垂直为0)；C为颗粒的质量浓度或数密度。

Chen和Lai[85]基于简化的三层模型，在考虑了布朗扩散和湍流扩散、重力、库仑力以及虚假惯性力的基础上，建立了一个修正的费克定律方程，并提出一种新的颗粒漂移通量模型用于数值模拟室内颗粒的分布与沉降[86]。付峥嵘[87]提出的解析法模型能很好地预测通风空调管道充分发展湍流段中颗粒的沉降规律。扩散惯性模型[88]能预测湍流中颗粒的扩散和沉降规律。两层分区的湍流模型能很好地预测圆管内纳米颗粒的沉降速度[89]。Guichard等[90]提出了用粒径分布矩表示的颗粒输运和沉降模型。

当颗粒Stokes数很小且无外力作用时，颗粒因布朗扩散和湍流扩散迁移到壁面[6, 91-92]。当存在温度梯度时，热泳力对颗粒沉降也起到重要作用。研究结果表明，热泳力的存在能增强对湍流扩散敏感的颗粒的沉降[93]。

Lin等[94]研究了不同Reynolds数下圆球形纳米颗粒通过弯管时的穿透率，给出了8～550 nm颗粒的穿透率与综合参数的关系式，该参数包括了Schmidt数、Dean数和管道长度的作用。他们还进一步研究了圆柱形纳米颗粒通过弯管时的穿透率[95]，其中穿透率(PE)与Stokes数(St)的关系如图7[95]所示，可见随着Stokes数的增加，穿透率先增大然后减小；同时，穿透率随着Dean数(De)、Reynolds数(Re)、颗粒长径比的减小而增大。基于数值模拟的数据，他们建立了穿透率与Dean数、Reynolds数、颗粒长径比、Stokes数之间的关系。

图7 穿透率与St和Re的关系(长径比为8，De=1 862)[95]

Ounis等[96]对槽道两相湍流场的直接数值模拟表明，颗粒布朗运动效应和拟序涡流形成的往壁面的流动导致了亚微米颗粒在壁面的沉积，颗粒的沉积数量和沉积速度随着颗粒直径的减小而增加。Wu和Young[97]研究了小颗粒在壁面上的沉积，图8[97]给出了颗粒密度的分布，可见直径为0.01 μm的最小颗粒占据了整个流场，因为它们具有很好的跟随性，这种尺度颗粒的沉积主要是由扩散引起的，颗粒沉积在叶片的吸力面和压力面上。然而，即使这么小的颗粒，惯性也起着重要的作用，因为压力面的颗粒密度高于吸力面。

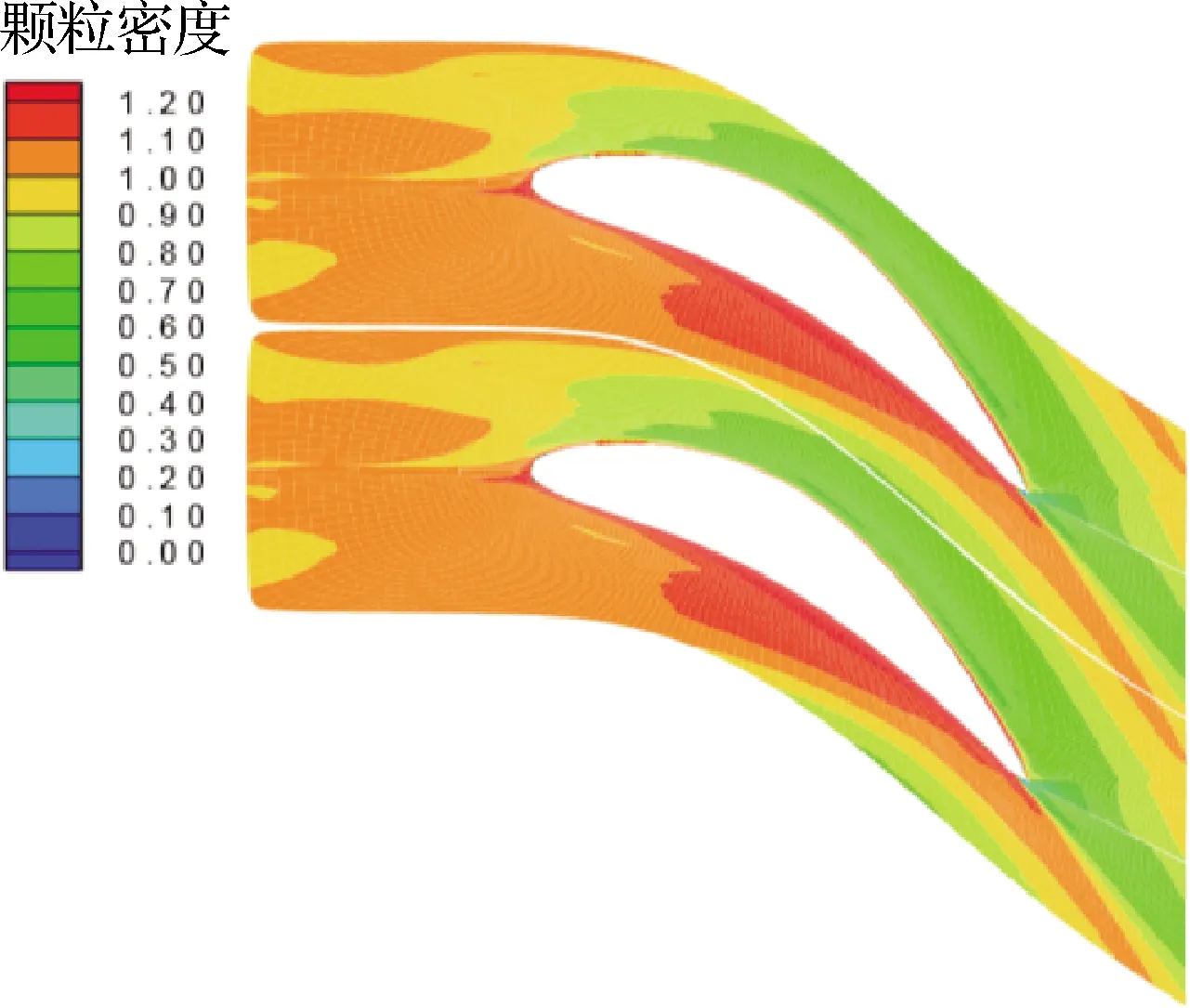
图8 颗粒密度等值线图[97]

呼吸道内颗粒的沉积也是人们关注的热点。Mina等[98]研究了纳米颗粒在人体呼吸系统上部的沉积，其结果如图9[98]所示，研究结果表明，颗 粒越小其扩散性越强、颗粒浓度衰减就越快即颗粒的沉积量就越大。

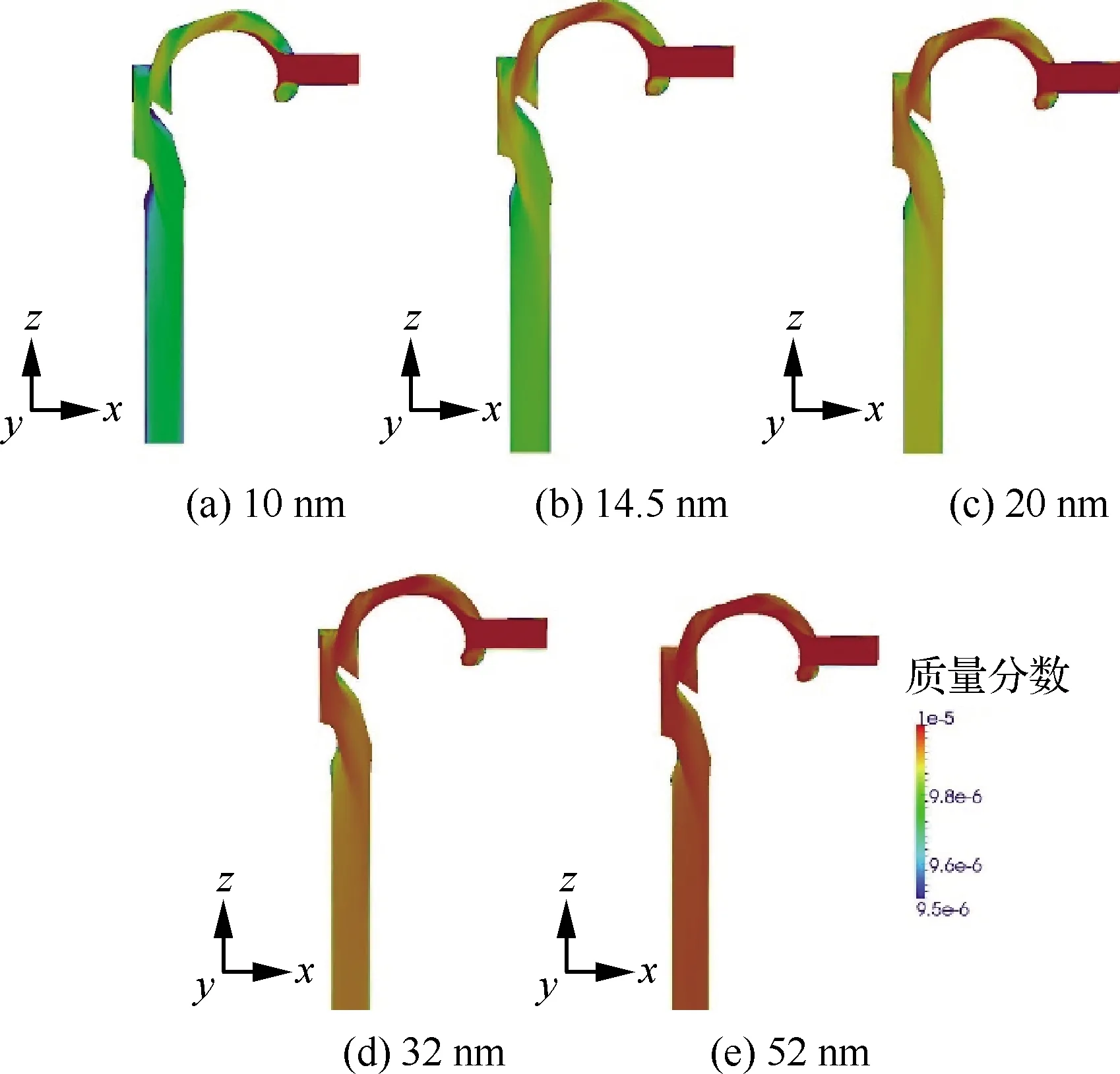
图9 不同尺度颗粒的质量分数分布[98]

5 结论与展望

本文回顾了含纳米颗粒气固两相湍流场中颗粒的生成、凝并、破碎、沉降的部分研究状况，主要研究结果归纳如下。

1)颗粒在气体环境中的生成是气相化学反应产生的可冷凝蒸汽物质因表面冷却、绝热膨胀或混合、湍流混合或化学过程产生的过饱和所导致；燃料含硫量和相对湿度的增加或环境温度的降低均导致颗粒生成率以及平均粒径增加；随着湍流度的增大，颗粒的分布变宽、平均直径变小；温度较低的区域更容易导致颗粒成核。

2)导致颗粒碰撞凝并的原因包括布朗运动、湍流剪切作用、速度梯度、差异沉降；颗粒的凝并取决于颗粒的尺度和流场的特性；布朗凝并通常发生在小于1 μm的颗粒，湍流凝并通常发生在粒径为1 μm以上的颗粒或者是高湍流情况下的亚微米颗粒；小尺度的流场脉动对颗粒的凝并既有促进也有抑制作用，但后者更为明显；颗粒凝并受初始颗粒分布及湍流扩散控制；湍流场对颗粒凝并的影响除了湍流强度的因素外，还体现在由湍流脉动所引发的颗粒数密度的脉动。

3)颗粒凝并后形成尺度较大的团聚体容易在流场剪切和其他因素作用下发生解体破碎；剪切破碎是导致颗粒破碎的主要因素；有效破碎系数取决于剪切率和颗粒的体积分数，体积分数越大、剪切率越高，颗粒越容易破碎；当剪切率一定时，颗粒的体积分数增加，稳态的颗粒尺度减小；进出口压差越大，颗粒破碎程度越高。

4)颗粒的沉降取决于颗粒尺度、形状和流体性质等因素；导致颗粒沉降的因素有重力、扩散、惯性撞击、电场和热迁移等；湍流场中颗粒的沉降与黏性底层和过渡层中的参数密切相关；粒径较小颗粒的沉降主要因布朗扩散和湍流扩散所致，粒径较大的颗粒主要受其惯性和重力支配；当存在温度梯度时，热泳力对颗粒沉降起到重要作用。

如前所述，虽然含纳米颗粒气固两相湍流场的研究已取得了许多有价值的成果，但仍有一些问题有待于进一步研究。

1)湍流脉动对于纳米的扩散有明显的影响，需要建立由湍流脉动导致的纳米颗粒扩散项的表达式。

2)湍流脉动不仅对颗粒的速度有影响，也会导致颗粒数密度的变化，所以要建立由湍流脉动导致的纳米颗粒数密度增减项的表达式。

3)纳米颗粒两相流场的动力学特性覆盖较大的空间和时间尺度，需要建立具有不同特征尺度作用的纳米颗粒两相湍流场较完整的数理模型并付诸于实际应用。