非等强度多道冲击波作用下空泡溃灭机制分析

吴汪霞，王兵，王晓亮，刘青泉,*

1.北京理工大学 宇航学院，北京 100081 2.清华大学 航天航空学院，北京 100084

火箭燃料泵中发生的空化及其溃灭[1-2]、超燃冲压发动机内激波串与油气混合物的相互作用[3-4]，以及生物医学领域的体外冲击波疗法中[5]均存在着多重冲击波与空泡的作用问题。空泡在多重波系的作用下会发生复杂而剧烈的动力学瞬变行为，这一过程还伴随着流动状态的剧烈变化，其对设备稳定性与作用效果等影响显著，这一问题也是可压缩多相流中的一个重要问题。

空化现象在工业生产与工程应用中广泛存在且应用前景广阔，是两相流体力学的一个物理基础问题，一直以来受到各个领域学者们的密切关注[6-9]。空化演化尤其是空泡溃灭过程往往伴随着复杂的现象且引起流场物理量剧烈变化[10]，学者们对此展开了大量研究。研究发现，空化泡的溃灭大致分为2类：对称溃灭(也称为瑞利溃灭)与非对称溃灭。当空化泡处于各向同性的流场中，则整个空泡均匀地受到周围流场作用而引发其发生对称变形行为，即空泡演化过程中一直维持其初始的形状，对于初始球形空泡其溃灭过程中一直保持球形。对于空泡的对称溃灭行为，早期的学者开展了一系列的理论研究[11-13]，由动量方程出发给出了空泡界面随时间变化的理论表达式(R-P方程)[7]，并描述了空泡压缩到最小半径而后发生反弹、释放压力波等现象。

然而，在实际情况中往往由于存在多重波系、相邻空泡、流体界面以及壁面等引起流场非对称的因素，因此很难保证空泡的完全对称溃灭，绝大多数情况下空泡为非对称溃灭[14-16]。在非对称溃灭情况下，由对称条件推导得到的界面演化理论表达式失效，并且溃灭压力波的产生机制也与对称工况明显不同。因此，对于空泡的非对称溃灭行为学者们开展了一系列实验与数值研究。借助于高速摄影和纹影技术，Tomita等[17-18]观测了壁面附近空泡的溃灭过程，并讨论了其非对称溃灭行为可能对壁面造成的损伤；Blake和Gibson[16]研究了自由表面附近空泡的非对称溃灭；Dear[19]和Bourne[20]等则对空泡在单一冲击波作用下空泡的非对称溃灭过程进行了观测，他们均观测到空泡非对称溃灭过程中会存在内卷现象并产生局部射流。而后，得益于计算机计算水平的进步，Ball[21]和Hawker[22-23]等通过数值方法模拟了单一冲击波等非对称因素作用下空泡的整个溃灭过程，解释并分析了流场中各介质中各种波系的产生、演化机理，揭示了空泡非对称溃灭以及溃灭波的产生机制。

很多实际问题中，通常存在不只一个空泡，甚至出现密集的空泡云，空泡群溃灭过程中会产生复杂波系，因此空泡会受到不只一道冲击波的作用[24]，此外，在体外冲击波治疗中更是需要一系列冲击波连续作用于肌体以达到治疗效果[25]，因此有必要开展空泡在多重波系作用下溃灭演化机理的研究。然而，迄今为止，针对空泡在多重冲击波作用下溃灭特性的研究仍然十分不足。本文基于可压缩两相流模型，分别对液体中空泡在单一冲击波以及多重冲击波作用下的演化溃灭问题进行数值模拟研究，探讨单一/多道冲击波作用下空泡溃灭机制的异同，并进一步宏观地解析多道冲击波的作用效果。

1 物理系统

对于冲击波与空泡作用问题，本文考虑的物理模型如图1所示。初始时刻，半径R0=0.32 mm的空气泡静置于液态水中，流场初始压力p0为1个大气压，初始温度T0为293 K。随后，由气泡右侧由右向左传播而来一系列冲击波。对于每一道冲击波，参考Johnsen和Colonius[26]的工作，冲击波波形的解析式为

图1 不同分布冲击波与液体中空泡作用示意图

p(t)=p0+2pWe-αtcos(ωt+π/3)

(1)

式中：p0为初始环境压力；pW为冲击波锋面压力值；其他参数的设置参考文献[27]。本文考虑了单一、2道和3道冲击波分别与空泡作用的3种工况，每道冲击波的宽度均为Δl(Δl=R0)。对于单一冲击波作用的情况(W1)，冲击波幅值pW1=420 MPa，波锋面对应的激波马赫数为1.14；对于2道冲击波作用的情况(W2)，冲击波幅值pW2=210 MPa，其波锋面对应的激波马赫数为1.07，其幅值为pW1/2；对于3道冲击波作用的情况(W3)，冲击波幅值pW3=140 MPa，其波锋面对应的激波马赫数为1.05，其幅值为pW1/3。

2 模型方法

为了有效模拟液体中多个空泡在波系作用下的非对称溃灭现象，并捕捉各个空泡的界面变形，本文采用欧拉框架下的多组分可压缩两相流模型[28-29]，控制方程为

(2)

式中：αk和ρk分别表示k组分的体积分数和密度；u、p、E和e分别表示速度、压力、总能和内能，总能表示为E=ρe+ρ|u|2/2，各组分体积分数之间满足约束条件：

(3)

本文采用的状态方程为刚性气体状态方程(SG-EOS)，状态方程的详细表达式以及各组分状态参数的设置参见文献[28]。由于本文考虑的空泡为空气泡，且主要研究冲击波作用下空泡变形溃灭的演化行为，因此忽略相变过程的影响。关于考虑相变情况下激波与空泡作用问题的研究可以参考文献[30]。

本文采用了有限体积方法对控制方程进行离散，使用高精度的变模板点加权基本无振荡差分(Incremental Stencil Weighted Essentially Non-Oscilatiory, WENO-IS)算法[31]进行重构，使用Harten-Lax-van Leer-Contact(HLLC)近似黎曼求解器求解黎曼问题[32]，时间方向采用三阶Runge-Kutta方法求解。由于本文研究对象的雷诺数Re与韦伯数We均为103以上的量级，因此忽略黏性与表面张力的影响，如果想要模拟更加宽泛的物理问题并得到更精确的结果，需要使用 Navier-Stokes 模型或者其他动理学模型[33-34]。由于该问题为轴对称问题，因此本文的数值计算中只考虑一半的计算区域，所有算例初始时刻每个空泡半径有340个网格，并采用轴对称坐标进行所有算例的计算。

3 计算结果与分析

3.1 单一冲击波作用下空泡溃灭行为

本文首先研究了液体中单一冲击波与空气泡的作用问题。图2为考虑轴对称效应的二维数值结果，气液界面由黑色实线标出，液体区域显示了压力云图，气体区域则给出了密度纹影图。图2(a)～图2(f)分别对应无量纲时间t·(R0/cl)-1=0, 0.96, 2.44, 5.10, 5.68，6.43，其中cl为初始状态下液体的声速。

如图2(a)所示，初始时刻一道强度为pW1的冲击波(S)自空泡右侧传播而来。冲击波与空泡作用后使得空泡被压缩变形，同时冲击波在界面处发生了反射和透射，分别产生液相的反射稀疏波(R)和气相的透射激波(T)，如图2(b)所示。液体侧稀疏波的作用使得空泡右侧液体进一步加速，加剧空泡变形的同时伴随着液体侧再入射流的形成，同时，透射激波伴随着空泡的进一步变形在空泡内相互作用并来回反射，使得气相压力逐步升高[20]。在再入射流的作用下，空泡左右两侧界面发生撞击(图2(d))，而后空泡破碎并伴随着一系列压力波的产生(图2(e)～图2(f))，该过程即称为空泡溃灭，空泡溃灭过程产生的压力波即为溃灭波。

3.2 多道冲击波作用下空泡溃灭行为

本节进一步研究了2道、3道冲击波与空泡的作用问题，并与单一冲击波作用过程进行对比，分析不同工况下空泡变形溃灭机制的异同。图3～图5分别展示了2道强度为pW2的冲击波、3道强度为pW3的冲击波与空泡作用时不同时刻的数值结果，与图2类似，图中黑色实线为两相界面，液体相给出了压力场云图，气体相则给出了密度纹影结果。图3(a)～图3(f)分别对应无量纲时间t·(R0/cl)-1=0, 1.05, 2.05, 5.86, 6.29，7.13，图5(a)～图5(f)分别对应无量纲时间t·(R0/cl)-1=0, 1.61, 2.64, 6.48, 6.90, 7.66。

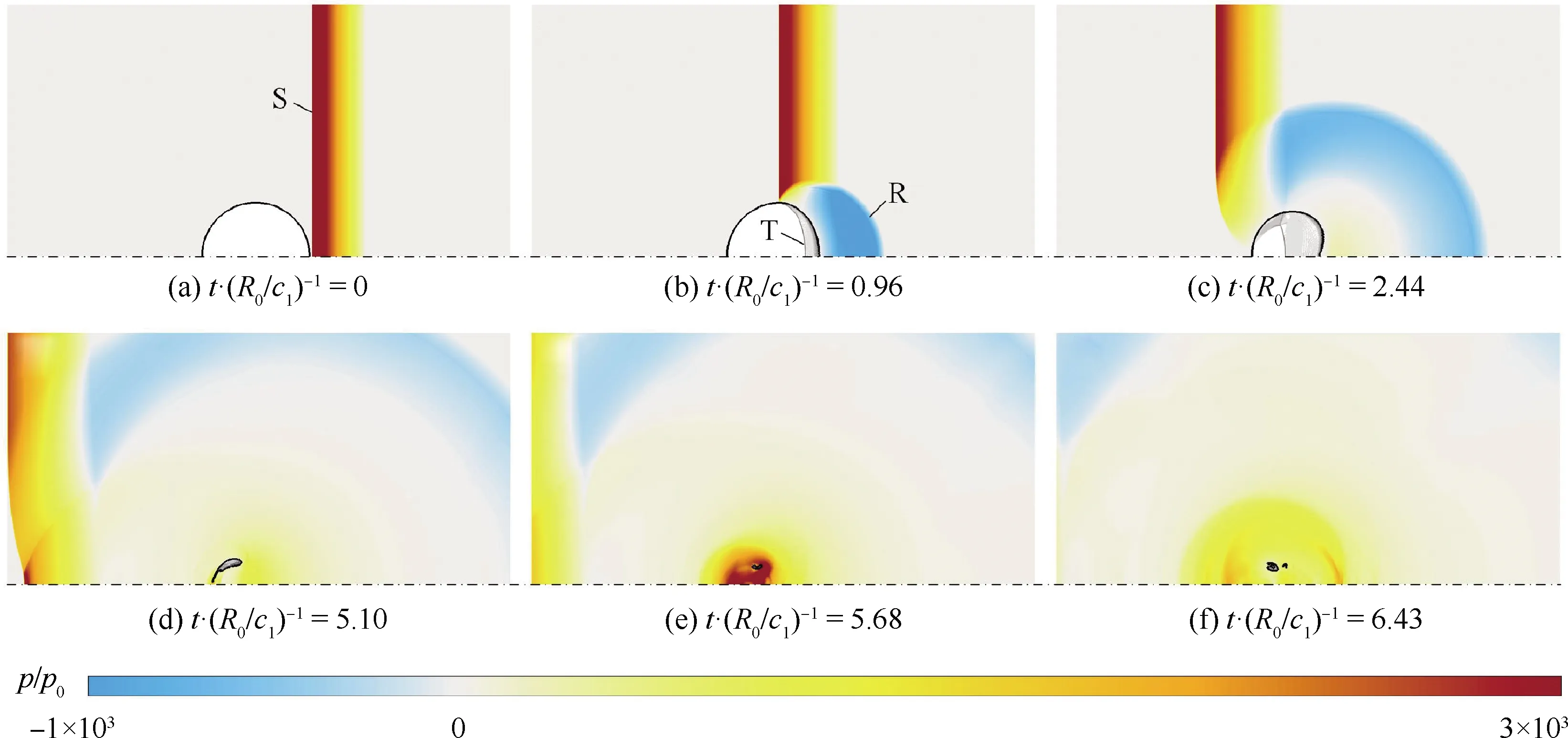
图2 强度为pW1的单一冲击波与空泡的作用过程

图3 2道强度为pW2的冲击波与空泡的作用过程

图4 2道强度为pW2的冲击波与空泡作用过程的局部放大图

图5 3道强度为pW3的冲击波与空泡的作用过程

如图3所示，2道冲击波S1、S2由空泡右侧由右至左传播并先后作用于空泡。与图2(b)类似，图3(b)显示当冲击波S1与空泡作用后使得空泡被压缩变形，同时冲击波在界面处发生反射与透射，液相侧产生向空泡外法线方向扩展传播的反射稀疏波(R1)，而气相侧则产生透射激波(T1)。此外，扩张传播的R1还会与随后的第2道冲击波S2相遇，使得S2被一定程度地削弱。随后，第2道冲击波S2与空泡作用，其在进一步加剧空泡变形的同时也在空泡界面处发生反射与透射，并产生反射稀疏波R2与透射激波T2。如图3(c)所示，此时在液体中共存着R1、R2这2道反射稀疏波，气泡内存在着T1、T2这2道透射激波。

随后，与图2中单一冲击波作用的工况类似，空泡在卷曲变形的同时伴随着液相侧再入射流的产生，最终在再入射流作用下空泡两侧界面发生撞击，空泡溃灭并产生一系列的溃灭压力波(图3(d)～图3(f))。通过对图2与图3的空泡溃灭及溃灭波的产生过程进行对比，可以看到，虽然2组工况下，空泡受不同分布冲击波作用，但是最终空泡从溃灭形态到溃灭的强度都十分相近。

为了更详细分析空泡在多道冲击波作用下空泡内波系的演化行为，图4进一步给出了2道冲击波作用下空泡变形过程的局部放大图(图3中红色虚线框区域)。图4(a)～图4(h)分别对应无量纲时间t·(R0/cl)-1=0.37, 1.07, 1.57, 2.68, 3.15, 3.79, 4.58, 5.40。如图4(a)～图4(c)所示，S1作用于空泡后，在R1及空泡的变形作用下流体加速，因此S2的锋面在作用于空泡前即发生了轻微弯曲变形。而后，S2作用于空泡并在空泡内部产生2道向下游传播的透射激波(T1、T2)。由图4(c)～图4(f)所示的透射激波在空泡内的传播演化过程可见，2道透射激波在空泡内传播时发生追赶，T2逐渐赶上T1并最终合并为1道更强的透射激波T0。而后，如图4(f)～图4(h)所示，T0继续传播，并在空泡界面来回反射，产生一次反射透射激波(R1-T0)、二次反射透射激波(R2-T0)等，直至空泡两侧界面在再入射流的作用下发生撞击。空泡内两道透射激波合并后的演化行为，与3.1节中较强的单一冲击波作用下波系的演化行为十分相似，这也解释了2个工况下空泡最终从溃灭形态到溃灭的强度都十分相近的原因。

进一步对空泡在S1、S2、S3这3道强度为pW3的冲击波作用下的演化过程进行分析。空泡首先受到冲击波S1的作用，并伴随着反射稀疏波R1与透射激波T1的产生。如图5(b)所示，R1在扩张传播的过程中会与冲击波S2、S3相遇，其强度均被一定程度地削弱。类似地，S2、S3分别先后作用与空泡，并在液相产生反射稀疏波R2、R3，气泡内产生透射激波T2、T3，同样地，先产生的反射稀疏波会与后续的冲击波相遇，并发生一定程度的相互削弱。如图5(c)所示，此时在液体中共存着R1、R2、R3这3道反射稀疏波，气泡内存在着T1、T2、T3这3道透射激波。

由图5(d)～图5(f)可以看到，在3道强度为pW3的冲击波作用下，空泡的溃灭过程与之前2个工况均十分相似，均为在再入射流作用下两侧界面撞击空泡溃灭，并产生一系列溃灭波。可以看到，在3个工况下，虽然空泡受到3组不同分布的冲击波的作用，最终空泡溃灭时的溃灭波分布与强度均基本相同。

当冲击波扫过气泡时，会在气液界面诱发 Richtmyer-Meshkov不稳定性[35]，这一现象在本文的数值结果中也有所体现，在图2～图5中均可看到激波与空泡作用后，空泡界面出现了Richtmyer-Meshkov不稳定性诱发的小的不稳定结构，然而对于本文所考虑的问题，这一结构对空泡溃灭强度的影响并不显著，因此在此不对其进行详细讨论。

3.3 空泡溃灭强度分析

为了进一步探讨分析冲击波与空泡溃灭强度的影响规律，本节分别给出了2组不同分布、不同强度冲击波与空泡作用时流场最大压力随时间的详细分布曲线。图6(a)展示了与第1节对应的3个工况下的压力最大值(pmax)曲线，图6(b)则展示了冲击波幅值为630 MPa的单一冲击波作用(W1′)、冲击波幅值为315 MPa的2道冲击波作用(W2′)和冲击波幅值为210 MPa的3道冲击波作用(W3′)3个工况下的压力最大值曲线。

图6 不同分布、不同强度冲击波与空泡作用时流场的最大压力随时间变化曲线

由2组压力最大值分布曲线均可以看到，当pW1=2pW2=3pW3时，单一冲击波与多道冲击波作用时压力最大值分布曲线十分相似，空泡溃灭诱发的压力峰值也基本相当。此外，空泡溃灭的时间差距也不大，具体而言，单一冲击波作用下空泡最早溃灭，2道冲击波作用下空泡溃灭又早于3道冲击波作用的工况。在空泡溃灭之前，多道冲击波与空泡作用的效果近似等于强度为多道冲击波强度之和的单一冲击波的作用。然而，对于单一冲击波工况，空泡更早地受高强度冲击波作用，因此空泡变形相对于多波累积作用工况稍快，空泡溃灭也稍早。

4 结 论

本文对单一、2道、3道冲击波分别与液体中空泡的作用问题进行了数值研究，结论如下：

1)各道冲击波与空泡作用后会依次在空泡界面发生反射与透射，并依次产生相应的反射稀疏波与透射激波。

2)无论是单一或多次冲击波的作用，空泡均会发生内卷变形并伴随着液体侧再入射流的产生，在再入射流作用下空泡最终溃灭并产生一系列的溃灭压力波。

3)在空泡发生溃灭前所受到多道冲击波作用下的溃灭行为及溃灭波强度，均近似于强度为多道冲击波强度之和的单一冲击波的作用。