流动聚焦装置微液滴生成及三维结构演化

王燕令， 张常青， 任敏， 刘鹤， 陈华， 吴学红

(1. 郑州轻工业大学能源与动力工程学院， 郑州 450001; 2. 郑州轻工业大学， 食品生产与安全河南省协同创新中心， 郑州 450001)

液滴微流控技术是指在微米乃至纳米尺度内控制微液滴流动的技术[1-2]，可广泛应用于生物化学[3]、材料合成[4]、药物研发[5-6]、医疗诊断[7-8]等领域。精确调控微流控芯片中的液滴生成可提高测试精度并加快反应速率[9-10]，因此，构建微液滴三维结构演化预测模型对精确调控液滴生产至关重要。

目前关于微液滴结构模型的研究多数是基于实验结果进行预测，该类模型对于不同流型适用性并不高[11-12]。Cubad等[13]针对喷射流型和滴落流型液滴进行了间接实验测量，认为液滴体积与分散相和连续相的流体物性、流动参数以及通道几何形状有关。崔艺文等[14]通过改变流动聚焦装置中喉部长度和宽度实现对液滴体积的控制。鲍鲁威等[15]通过对T形通道内的压力测量，提出当分散相压力大于连续相压力时，通道生成液滴的体积更趋于稳定。Glawdel等[16-17]将液滴弧状表面简化为平面，对T形通道微液滴生成中挤压流型进行了建模分析，该模型对于微液滴体积计算中易引起较大误差。Chen等[18]基于截面形状对液滴建立模型，同样采用了Glawdel建模方法。Wehking等[19]假设液滴两端由无数切片组成，其体积可以近似表示为液滴两端的面积乘以切片的宽度，但该模型尚未实验验证。

此外，液滴微流控实验采集的多是微液滴的二维形貌，其对应三维几何结构特征的演化规律研究较少。构建合理的微液滴三维结构预测模型，对精确控制液滴体积大小非常必要。现基于多模块分区建模思想，考虑微液滴断裂阶段和稳态过程的结构演化，提出一种描述流聚焦通道内液滴生成过程的三维几何结构演化模型，该模型不仅适用于液滴尺寸大于通道宽度的挤压流型，也适用于液滴尺寸略小于通道宽度的滴落流型和喷射流型。同时，基于实验观测结果进行模型优化，提升模型预测精度。

1 微液滴生成实验测量

1.1 实验系统

图1为微液滴生成实验装置示意图，实验设备包括高精度注射泵(Centoni neMESYS)、微流控芯片、高速摄像机(PCO Dimax HS)、数据采集系统等。互不相溶的两种液体(分散相和连续相)经注射泵分别进入微流控芯片，在流动聚焦区域内分散相被连续相挤压从而生成液滴。

图1 微液滴生成实验装置Fig.1 Experiment device of droplet generation

1.2 微液滴生成

聚二甲基硅氧烷PDMS(polydimethylsiloxane)与固化剂以质量比10∶1混合后，采用真空磁力搅拌器排出气泡并混合均匀，浇筑于掩模版上，放置于真空干燥箱内，90 ℃加热45 min后PDMS凝固，取出并切割打孔，经氧等离子体处理后与玻璃键合，经175 ℃烘烤4 h后取出静置，使得微流控芯片通道转变成疏水性壁面。实验用微流控芯片分为两组：上游孔径wor=25 μm和wor=75 μm，实验流动聚焦结构如图2所示。

实验中连续相采用低黏度矿物油(M5904，Sigma)，分散相是去离子水，两相界面张力经测量为5.3 mN/m。图3所示为三种分散相与连续相的体积流量比(Qd∶Qc=1∶1，Qd∶Qc=1∶2和Qd∶Qc=1∶4)下微液滴的生成，包括断裂阶段与稳态流动阶段微液滴形状。连续相流量分别为50、100、200 μL/h。采用ImageJ软件对图片进行测量计算。

图3中显示对于孔径wor=25 μm的通道，当流量增加时，生成的液滴流型逐渐从挤压流型转变为滴落流型和喷射流型，对应的体积计算模型随之发生变化。实验同时测量了wor=75 μm通道内的微液滴生成，其规律与wor=25 μm通道类似。

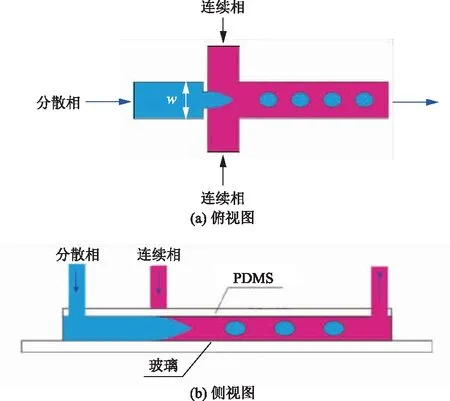
图2 实验流动聚焦结构.Fig.2 Structure of the flow-focusing device

图3 流动聚焦通道微液的生成(wor=25 μm)Fig.3 Droplet generation in flow-focusing device(wor=25 μm)

2 微液滴三维模型构建

2.1 微液滴流动聚焦生成过程形变演化

图4为矩形截面通道内微液滴生成及其三维结构示意图。互不相溶的两种液体分别作为分散相和连续相流体，分散相流体Qd从左侧进入通道，被上下通道内连续相流体Qc在流动聚焦区域挤压断裂，生成微液滴流出。图4为挤压流型微液滴生成实验俯视图，此流型下微液滴尺寸大于通道宽度。液滴生成后在微通道内流动，受最小表面能影响，其表面会收缩成半径为h/2的圆弧。Glawdel借鉴T形通道微液滴结构预测模型[20]，指出流动聚焦微液滴的截面是由两个r=h/2的半圆区域与中间矩形区域组成[14-15]，液滴体积计算可简化为

(1)

式(1)中：Ap为图4中液滴的投影面积；h为通道高度；l为液滴投影截面周长。

考虑到液滴在垂直高度方向其表面并非柱状平直，而是有一定弧度的存在，通过式(1)计算得到的液滴体积整体偏大。微液滴生成过程中，其液滴稳态流型主要包括挤压流型和滴落流型，模型如图5所示。根据不同流量比下的液滴形状，针对微液滴生成断裂过程和下游稳态流动时其三维结构演变进行探究，建立了断裂阶段和稳态阶段的数学模型，采用多模块分区建模计算的方式，在模型计算时采用旋转体积分方式，并修正锥形不规则斜面计算引入的计算误差。

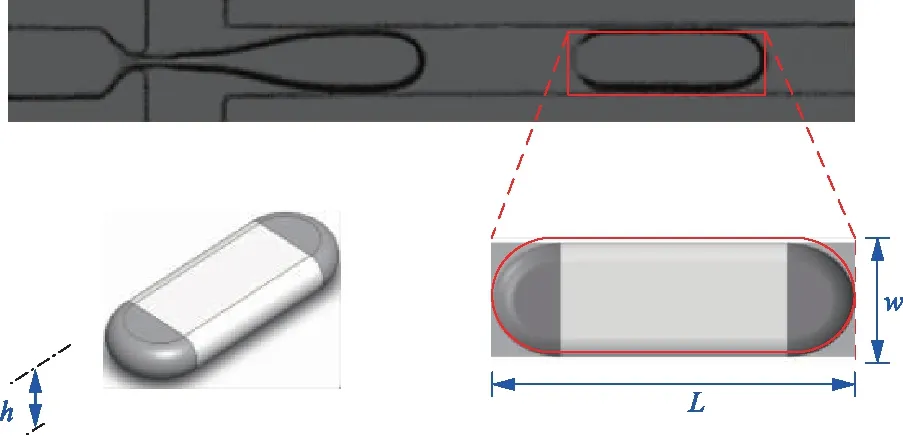
图4 液滴生成及其三维结构Fig.4 Droplet generation and the three-dimensional droplet structure

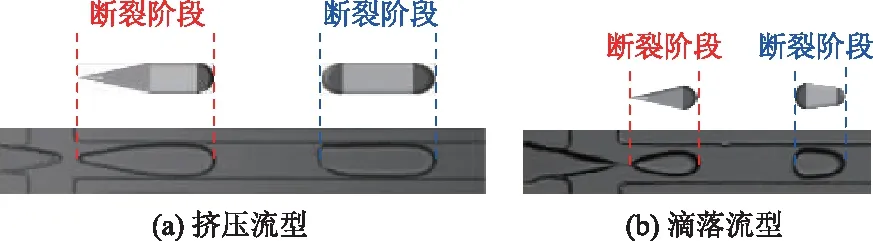
图5 流动聚焦微液滴生成Fig.5 Droplet in the flow-focusing device

2.2 液滴断裂阶段三维结构演化模型

在微液滴断裂截面，分散相液体受到连续相液体的挤压作用，在主通道方向逐渐收缩至临界直径wpinch后断裂。在较低的毛细数Ca下，液滴断裂时剪切力影响较小，可以忽略。断裂过程的主要驱动力是液滴前后的流动压降。当液滴颈部与其顶部的Laplace压力相等时，无法驱动液滴向前运动，上游分散相液体开始驱动液滴向下游运动，液滴断裂。此时由Young-Laplace方程，有

(2)

式(2)中：Rneck为液滴颈部半径；γ为界面张力。由于Rneck≫wpinch，可得

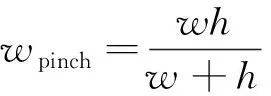
(3)

由于液滴形状受到通道几何形状限制，在通道壁面约束下液滴体积收缩成最小表面能的形状，即r=h/2的圆弧状。根据实验测量结果，断裂界面一般可以分为两种情况：①当Qd∶Qc≤1∶4时，液滴内部包含一个平直拉伸段，即拉伸长度λ≠0，如图6(a)所示；②当Qd∶Qc>1∶4时，液滴拉伸长度λ=0，此时液滴形似锥体，如图6(b)所示。将断裂阶段液滴体积模型分为a～f共6个模块：a部分为一圆台，主要考虑到液滴颈部受力平衡时开始发生断裂，其俯视截面与收缩段整体截面相似，b和c部分是倾斜的半圆柱，d部分是为三棱柱，e部分则是一个类椭圆柱体，其拉伸长度为λ，f是一旋转体。表1给出了断裂阶段液滴a～f各分段模块体积的计算方法和公式。

综合表1，断裂阶段液滴体积为

V=Va+Vb+Vc+Vd+Ve+Vf

(10)

图6 断裂阶段液滴体积模型分块划分Fig.6 Volume block model of the droplet at the breakup stage

表1 断裂阶段液滴体积分块计算Table 1 Volume calculation of droplet blocks at the breakup stage

2.3 液滴稳态流动阶段三维结构演化模型

液滴在下游流动时，连续相流体对液滴的挤压作用已不足以引起液滴表面产生明显形变，液滴前后两端的形状较为稳定。

根据实验测量结果，稳态流动时一般可以分为两种情况：①当连续相流量较大(Qd∶Qc≤1∶4)时，液滴中部是前后界面有一定倾角的楔型柱体，即θ≠0如图7(a)所示；②当分散相流量较大(Qd∶Qc>1∶4)时，液滴倾斜角度θ=0，此时液滴尾部形状收缩减小，如图 7(b)所示。将液滴稳态阶段其体积模型分为a～e共5个模块：a和c部分均为旋转体，e和d部分是半圆柱或倾斜半圆柱，b部分是为矩形或楔型柱体，定义前段宽度Dup，尾部宽度Ddown。楔型柱体倾角θ计算公式为

(11)

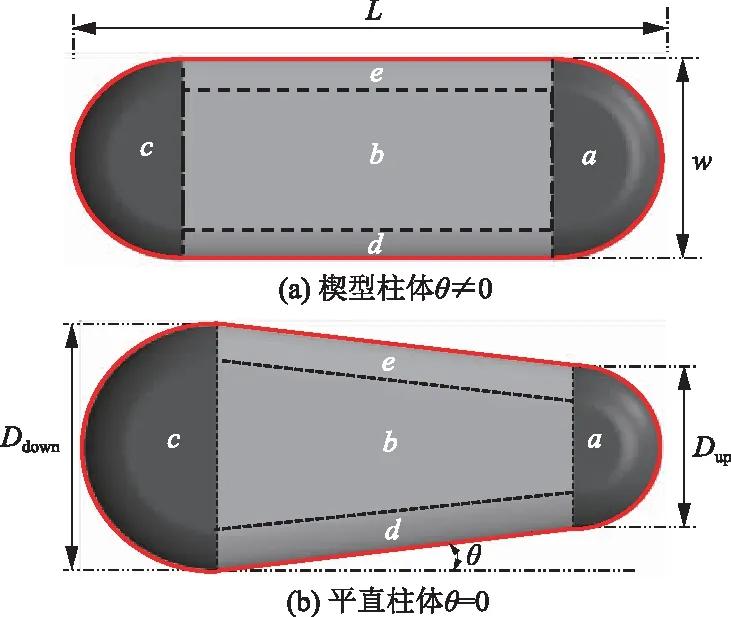
图7 稳态流动液滴体积模型分块划分Fig.7 Volume block model of the droplet at steady flow stage

综合表2各模块计算可得，稳态流动阶段液滴体积为

V=Va+Vb+Vc+Vd+Ve

(17)

表2 稳态流动阶段液滴体积分块计算Table 2 Volume calculation of droplet blocks at steady flow stage

3 模型验证与优化

3.1 模型验证

流动聚焦产生的微液滴在通道下游流动较为均匀，因此可以通过V=Qd/f来间接获得液滴的真实体积，其中Qd为实验设定的分散相体积流量，f为液滴生成频率，其大小可通过高速相机捕捉统计。本研究以液滴等效半径r来量化液滴体积的变化，其大小r=(3V/4π)1/3。

图8所示为模型计算结果和实验测量结果对比情况。可见，液滴断裂阶段，模型预测半径r*与实验液滴半径r相对误差δ为-11%～+17.5%，平均偏差为3.12 μm。其中相对误差δ= (r*-r)/r，平均偏差AD=(∑|r*-r|)/n。此外，不同孔径尺寸时，模型预测结果偏差也略有不同，wor=25 μm时计算显示最大偏差为+6.69 μm，而wor=75 μm则是最大偏差-6.49 μm。引起预测结果偏差的主要因素是断裂界面液滴在经历临界断裂点时，界面张力急剧变化使得液滴出现明显回缩现象，易造成液滴的测量长度整体偏小。当液滴处于下游稳态流动时，模型预测体积大小较实验结果普遍偏小，相对误差普遍分布在-20%～-35%，模型计算偏差趋势受孔径影响较小。综合对比可知，对于断裂阶段微液滴大小和实验测量值偏差较小，所构建的三维体积模型较为合理，能较准确描述断裂过程液滴的形貌特征。而对于稳态流动阶段液滴，构建的模型计算结果普遍偏小，可引入校正因子进行校正，对其三维模型加以优化。

图8 模型计算与实验结果对比Fig.8 Comparison of the volume model with the experimental results

3.2 稳态流动模型优化

受制于工艺限制，实验通道高度h均匀性难以精确控制，无法保证通道高度完全一致，导致液滴在通道内的真实长度难以反映在模型计算与实验对比的基础上，使得稳态流动模型计算数值普遍偏小，采用对稳态流动中间长度段进行修正，引入修正系数α，对式(13)、式(15)和式(16)进行修正，得

(18)

(19)

(20)

将修正后的公式代入计算表明，修正系数α=2.5时，模型偏差最小，如图9所示。

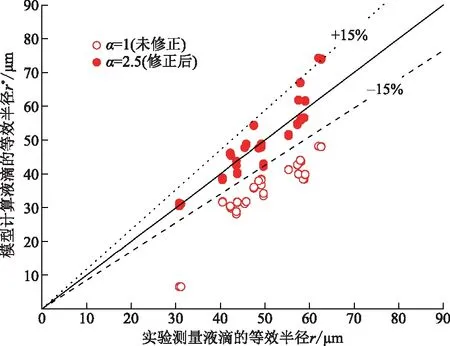
图9 稳态流动模型校正与实验对比Fig.9 Comparison of the revised volume model with the experimental results for the steady flow

修正后模型预测半径与实验液滴半径相对误差在-15%～+19.7%，平均偏差为3.61 μm，相较修正前明显改善。

4 结论

提出了描述流动聚焦装置中液滴在断裂阶段和稳态流动阶段的三维结构的方法，基于多模块方式分段构建了液滴结构预测模型。基于液滴宽度w、液滴长度L、液滴流动倾角θ和液滴中间段长度λ四个基本参数来描述液滴的形状和体积。模型考虑到液滴的三维曲面特征，利用分散相和连续相的质量守恒，可精确地预测液滴在形成周期中的结构特征。

对比液滴微流控实验测量结果可见，液滴断裂阶段时，模型预测与实验液滴半径相对误差δ在-11%～+17.5%，平均偏差为3.12 μm。wor=25 μm时计算显示最大正偏差+6.69 μm，而wor=75 μm则是最大负偏差-6.49 μm。针对稳态流动模型偏差较大的问题，引入了修正系数α对模型进行优化，修正后液滴半径相对误差在-15%～+19.7%，平均偏差为3.61 μm，相较修正前明显改善。