失效概率矩独立全局灵敏度分析的高效算法

蒋献，王言，孟敏

中国飞行试验研究院 技术中心飞机所，西安 710089

灵敏度分析主要衡量输入变量的不确定性对输出变量不确定性的影响程度。目前，灵敏度分析主要分为：局部灵敏度分析、区域灵敏度分析[1-3]以及全局灵敏度分析[4-5]。全局灵敏度分析以其能够从全局的角度反映输入变量不确定性对输出变量不确定性的影响程度而在工程设计及可靠性评估中广为应用。全局灵敏度分析方法主要有：非参数法[6]、方差灵敏度分析法[7-9]、基于概率密度函数的矩独立灵敏度分析法[10]以及失效概率矩独立灵敏度分析法[11-12]。目前，方差灵敏度分析法及基于概率密度函数的矩独立全局灵敏度分析的计算方法较为成熟，主要包括样本法[13-15]、矩方法[16-17]以及代理模型法[12,18-20]。

失效概率矩独立全局灵敏度分析主要衡量的是输入变量在其整个取值区域变化时对结构失效概率的平均影响程度。失效概率矩独立全局灵敏度分析结果可以起到指导可靠性优化设计的作用。文献[12]建立了失效概率矩独立全局灵敏度指标与方差全局灵敏度指标的关系。基于文献[12]，文献[21]提出了单层分析法来求解该指标，单层分析法是基于样本的方法且其计算量仍与输入变量的维数线性相关。文献[22]将极大熵及Nataf变换相结合提出了一种高效的分析算法，但由于Nataf变换仅适用于正态分布及小变异系数下的对数正态分布[23]，对非正态变量及大变异系数的对数正态分布的情况，文献[22]的方法将产生较大的估计误差。为避免使用Nataf变换，文献[17]将极大熵与三点估计结合，其计算过程仍是双层嵌套的过程。外层期望的求解采用三点估计，内层条件失效概率及无条件失效概率求解过程中的概率密度函数估计采用极大熵法，该方法的计算量较文献[22]的高，且计算精度依赖于三点估计对外层期望的估计精度以及极大熵方法中优化过程的准确性。

通过上述对已发展的失效概率矩独立全局灵敏度指标算法的分析，可以看出极大熵结合Nataf变换[22]算法的效率较其他算法都高，但Nataf变换的使用限制使得该算法具有了一定的局限性，因此为了继承该算法的高效性，同时又克服该算法的局限性，本文将乘法降维及Edgeworth级数展开的思想相结合，通过Edgeworth级数展开将输出的无条件及条件失效概率的求解转化为无条件及条件前四阶矩的求解，对于输出的无条件及条件四阶矩的求解，通过乘法降维推导了重复利用积分网格信息求解的策略，并通过重复利用积分网格内的信息求解外层积分。该算法的计算量(真实物理模型的调用次数)仅与无条件矩计算中积分网格的建立有关，条件矩及外层积分的求解都无需额外的计算量，且该算法避免采用Nataf变换，消除了Nataf变换所带来的限制以及避免了极大熵求解概率密度函数时的优化过程，提高了计算的准确性，且不失计算的高效性。

本文第1节简要回顾了失效概率矩独立全局灵敏度指标的定义。第2节详细介绍了本文所提的基于乘法降维结合Edgeworth级数展开的失效概率矩独立全局灵敏度求解算法。第3节通过分析航空发动机涡轮盘以及汽车前轴的失效概率矩独立全局灵敏度，说明了本文方法的准确性及高效性。第4节对本文进行了总结。

1 基于失效概率的矩独立全局灵敏度指标的定义

对于一个分析模型Y=g(X),Y为结构或系统的输出,X=[X1,X2,…,Xn]为结构或系统模型的随机输入，n为模型的输入变量个数,g(·)为模型的极限状态函数。失效概率的计算式为

(1)

式中：F为失效域，定义失效域为F={X:g(X)≤ 0}；fX(x)为输入变量的联合概率密度函数，x为变量X的实现。因此，式(1)亦可表达为极限状态函数的概率密度函数fY(y)在失效域的积分，即

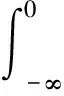
(2)

式中：y为变量Y的实现。

为衡量输入变量对结构失效概率的影响，文献[11]建立了失效概率矩独立全局灵敏度指标，其衡量的是无条件失效概率与条件失效概率的绝对差异的平均值，即

(3)

式中：i为第i个输入变量；Pf|Xi为Xi固定在其分布内某一实现值时输出的条件失效概率；条件失效概率Pf|Xi可以表示为极限状态函数的条件概率密度函数fY|Xi(y)在失效域内的积分，即

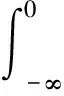
(4)

将式(2)及式(4)代入到式(3)中,可得

(5)

从式(5)可以看出，若能高效准确地求解输出的无条件及条件概率密度函数，以及外层期望，即可高效准确地分析得到失效概率矩独立全局灵敏度。在第2节中，本文详细介绍了所提的基于Edgeworth级数展开结合乘法降维的输出无条件概率密度及条件概率密度函数的求解算法。

2 基于乘法降维及Edgeworth级数展开的失效概率矩独立全局灵敏度高效求解算法

2.1 基于前四阶矩的Edgeworth级数展开法求解无条件及条件输出概率密度函数

根据Edgeworth级数展开法[24]，输出的无条件概率密度函数可以表示为

fY(y)≈

(6)

式中:

(7)

(8)

输出的条件概率密度函数可以表示为

fY|Xi(y)≈

(9)

式中:

(10)

(11)

其中：α1g、α2g、α3g、α4g为输出的无条件前四阶中心矩；α1g|Xi、α2g|Xi、α3g|Xi、α4g|Xi为Xi固定在某一实现值时输出的前四阶条件中心矩，无条件及条件前四阶矩的定义式为

(12)

(13)

从式(6)～式(11)可以看出，通过Edgeworth级数展开法，输出的无条件概率密度函数及条件概率密度函数的求解转换为求解输出的无条件及条件前四阶中心矩。对于输出的无条件及条件前四阶中心矩，本文在2.2节从乘法降维的角度推导了通过重复利用乘法降维计算输出无条件矩中所产生的积分网格中的数据同时求解输出条件前四阶中心矩及外层期望的计算式。

2.2 乘法降维求解输出的无条件前四阶中心矩

根据文献[16]，模型Y=g(x)可以近似表达为如下的一维变量函数的乘积形式，即

g(x)≈[g(μ)]1-n·

(14)

式中:μ=[μ1,μ2,…,μn]是输入变量X的均值向量，k(k=1，2，…，n)为输入变量的次序。

因此，通过式(14)输出的αp阶原点矩可以从一个n维积分近似转化为n个一维积分的乘积形式，即

(15)

表1 高斯积分网格Table 1 Gaussian integration grid

根据高斯积分，式(15)可以由式(16)计算得到，即

Mαpg≈gαp-nαp(μ)·

(16)

(17)

通过输出的前四阶原点矩求得输出的前四阶中心矩，即

(18)

2.3 乘法降维求解输出的条件矩

根据式(14)可以推导出输出的条件矩的近似计算式为

gαp-nαp(μ)gαp(xi,μ-i)·

(19)

根据高斯积分准则，式(19)可计算得

Mαpg|Xi(xi)=gαp-nαp(μ)gαp(xi,μ-i)·

(20)

fY|Xi(y)=MXi(g(xi,μ-i))

(21)

式中：MXi(·)是通过Edgeworth级数展开求解概率密度函数的过程，该过程无需额外的模型调用次数。

对于式(5)的外层一维积分，本文仍采用高斯积分求得。因此，式(5)可通过式(22)进行估计:

(22)

乘法降维求解矩的过程中对随机变量的分布形式没有限制，Edgeworth级数展开法近似概率密度函数的过程中也对随机变量的分布形式没有限制，因此本文所提算法在求解失效概率矩独立全局灵敏度中对随机输入变量的分布形式没有限制。

2.4 计算量

(23)

式中：p为输入变量中对称分布的个数。

3 算例分析

3.1 算例1：航空发动机涡轮盘

涡轮盘是航空发动机关键转动部件之一，在起动和加速过程中承受着巨大的离心力和热应力。加上机构形状复杂，在工作过程中容易出现应力集中部位，如榫槽槽底、销钉孔等。在工作一段时间后，可能在这些部位出现裂纹故障，如图1所示。某型航空发动机涡轮盘在工作时所受载荷为F=Cω2/2π+2ρω2J，ρ、C、ω和J分别是质量密度、系数、转动角速度和截面惯性矩，ω=2πn′,n′为转动频率。涡轮盘的强度极限为σs，截面积为A。建立涡轮盘破裂失效的极限状态函数为

g(σs,ρ,C,A,J,n′)=σsA/F

(24)

6个输入变量的分布参数如表2所示。根据乘法降维中求解一维变量积分的高斯数值积分法则建立求解整数矩的高斯积分网格如表3所示。根据式(23)计算的构建这高斯积分网格所需的模型调用次数为27次。通过重复利用表3中的信息，可以将输出的无条件前四阶矩、输出的条件前四阶矩及指标求解过程中的一维外层积分同时求得，所得失效概率矩独立全局灵敏度指标如表4所示。表4给出了双层MCS(Monte Carlo Simulation)法、文献[22]提出的极大熵结合Nataf变换法、文献[17]提出的三点估计结合极大熵法以及本文所提算法的计算结果。从表4的分析结果中可以看出，极大熵结合Nataf变换法在求解质量密度ρ及系数C的失效概率矩独立灵敏度指标

图1 航空发动机涡轮盘模型裂纹示意图Fig.1 Diagram of crack of aero-engine turbine disk model

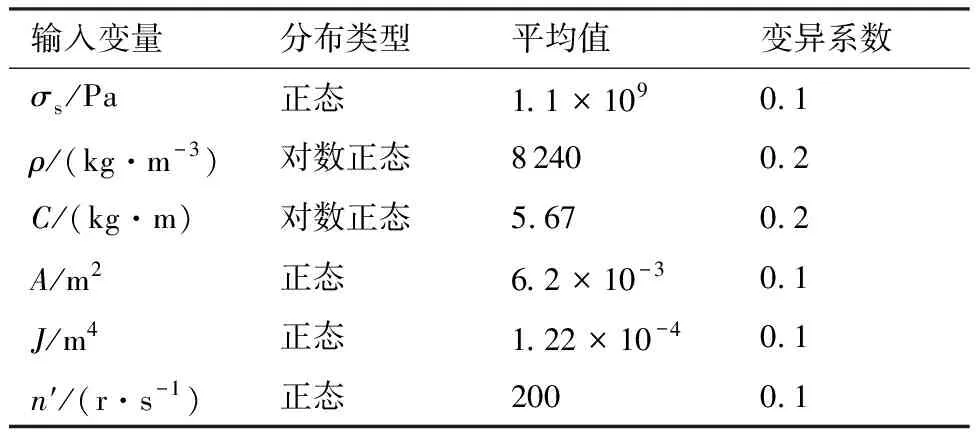
表2 基本变量分布参数Table 2 Distribution parameters of input variables

中出现了严重的错误，这是源于Nataf变换对大变异系数的对数正态分布的联合概率密度函数的近似不够准确。三点估计结合极大熵变换的方法得到的结果与双层MCS得到的结果较为接近，但其模型调用次数为390次。本文算法仅通过27次模型调用，就得到了与双层MCS较为接近的结果，其计算量仅为三点估计结合极大熵变换算法的6.92%。表4中也给出了双层MCS法、文献[22]所提的极大熵结合Nataf变换法、文献[17]提出的三点估计结合极大熵法和基于本文所提方法在分析失效概率矩独立全局灵敏度指标的计算耗时。从表4中可以看出本文所提算法的计算耗时较已有对比算法都少，主要原因是本文所提算法在概率密度函数估计中避免了优化过程且能重复利用无条件矩求解过程中的积分网格内的信息，同时求得输出的条件矩及指标求解过程中的外层积分。双层MCS方法的计算时间最长，极大熵结合Nataf变换算法较三点估计结合极大熵算法的计算时间长，其原因在于极大熵结合Nataf变换的算法中不仅存在优化过程估计概率密度函数的耗时，同时还存在Nataf变换中求解非线性方程的耗时。因此，从计算耗时的角度再次说明了本文所提算法的高效性。6个随机输入变量的基于失效概率的矩独立全局灵敏度的排序为n′>ρ>A>σs>J>C，该排序可用于指导该结构的可靠性优化设计。

表3 航空发动机涡轮盘的高斯积分网格Table 3 Gaussian integration grid of aero-engine turbine disk

表4 航空发动机涡轮盘的数值计算结果Table 4 Numerical results of aero-engine turbine disk

3.2 算例2：汽车前轴

图2所示为一汽车前轴示意图，故危险截面常发生在工字梁上，其截面形状如图2所示。已知危险截面的最大正应力为σ=M/Wx和τ=T/Wρ，其中M和T分别为前轴所受的弯矩和转矩，Wx和Wρ分别为结构的截面系数和极截面系数，且有

(25)

Wρ=0.8bt2+0.4[a3(h-2t)/t]

(26)

式中：a、b、h、t为工字梁几何参数。

图2 汽车前轴示意图Fig.2 Schematic diagram of automobile front axle

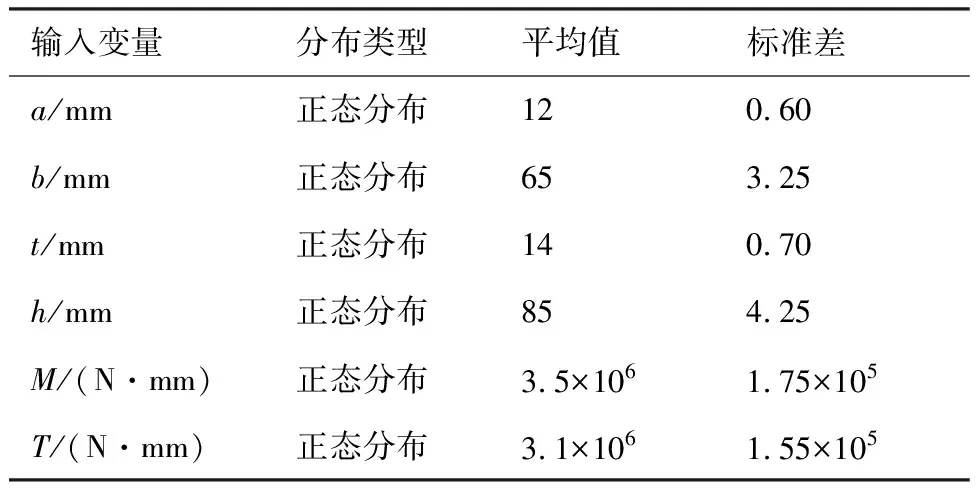
表5 输入变量的分布参数Table 5 Distribution parameters of input variables

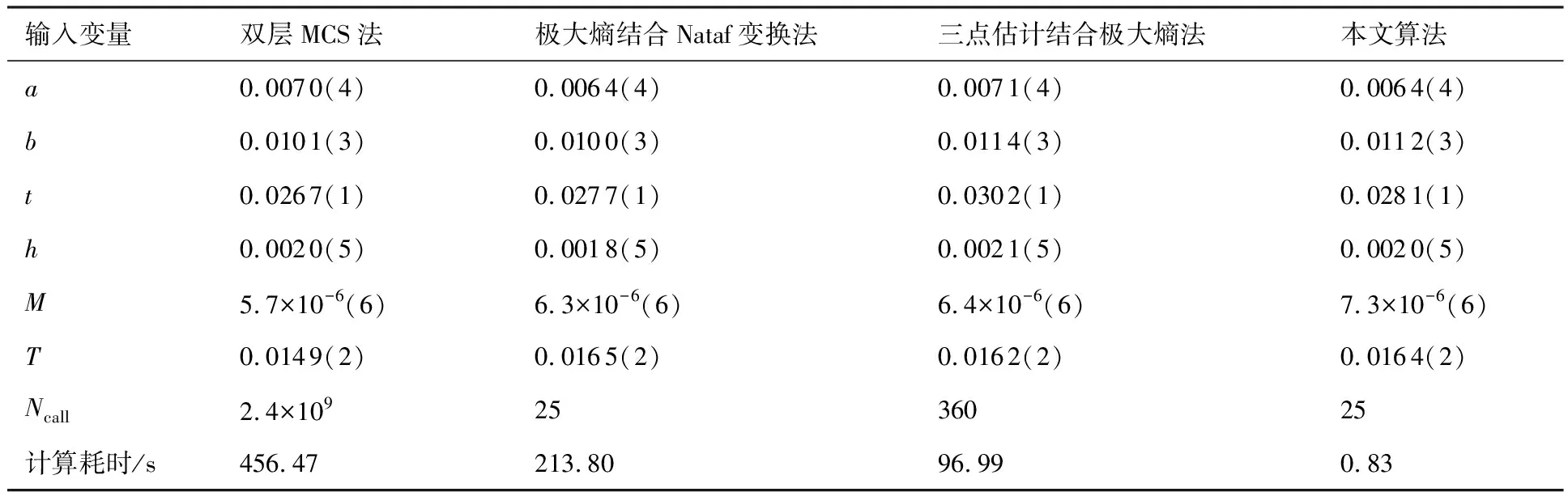
表6 汽车前轴的数值计算结果Table 6 Numerical results of automobile front axle

4 结 论

本文针对可靠性优化设计中较为关键的可靠性全局灵敏度分析指标，即失效概率矩独立全局灵敏度指标，提出了高效准确的计算方法。本文推导了如何重复利用乘法降维估计输出无条件前四阶矩的输入-输出样本来估计输出的条件前四阶矩以及外层的输入变量的一维积分。通过理论推导及算例分析，得到如下结论：

1) 本文所提算法的模型调用次数仅为乘法降维估计输出无条件前四阶矩的模型调用次数。

2) 本文所提算法的计算量与极大熵结合Nataf变换的计算量一致，但避免使用Nataf变换从而克服了Nataf变换使用过程中所带来的计算误差以及避免了Nataf变换的局限性。对于极大熵结合Nataf变换法无法使用的大变异系数的对数正态分布情况，本文所提算法得到了较为精确的结果。

3) 较极大熵结合Nataf变换，本文所提算法也无需优化过程，从而避免了优化结果的不稳定性对灵敏度分析结果的影响。

4) 在计算耗时上，本文算法的计算耗时对比于已有的对比算法都要少，主要原因是本文所提算法无需优化拟合输出的概率密度函数以及Nataf变换，从而避免了优化过程的耗时以及Nataf变换中求解非线性方程过程的耗时。

5) 由于本文算法仅需明确输入输出关系，因此，不论显式输入输出关系还是隐式输入输出关系，本文所提算法都适用。