适用于涡激振荡问题研究的并行高精度方法

邱滋华，徐敏, *，张斌，梁春雷

1. 西北工业大学 航天学院，西安 710072 2. 乔治华盛顿大学 机械与航空工程系，华盛顿特区 20052

因材料特性和流体作用力形式的不同，流体流过固体结构时可以引发多种形式的振动[1]。例如，桥梁或机翼的颤振和驰振等不稳定振动；高楼或电线的抖振和涡激振荡(Vortex-Induced Vibration, VIV)等共振振动；多边形截面和直升机旋翼的自旋转动。在上述诸多形式中，钝体的涡脱落及其VIV现象由于具有广泛的工程应用，且较为基础和易于实验，近年来持续受到广泛关注[2-5]。VIV常发生在钝体绕流伴随涡脱落的情况下，不稳定的涡施加振荡力于物体表面，从而引起振动。当涡脱落的频率接近结构的自然频率时，会发生共振，振动的幅值也会大大增加。

Feng在1968年进行的实验被认为是第一批现代VIV研究之一[6]，在其研究中，圆柱只能垂直于来流振动。Khalak和Williamson在实验研究了质量和阻尼对单个圆柱振动的影响后，发现相比于经典的Feng式响应，参数的改变会使得响应模式更为丰富[7-8]。Mittal和Kumar[9]、Jeon和Gharib[10]、Jauvtis和Williamson[11]、Prasanth等[12]研究了圆柱的二自由度涡激振荡，发现沿来流方向的振动幅值比垂直来流方向的振动幅值小若干个量级。Yao和Jaiman[13-14]提出了适用于涡激振荡问题研究的降阶模型，并研究了针对VIV的反馈控制算法。以上研究发现，VIV对于系统的物理参数非常敏感，表现出了极强的非线性，其响应机理还有待进一步研究。

VIV问题的数值模拟主要存在以下几个难点。首先，VIV对于系统的物理参数非常敏感，较小的参数变化也有可能引起响应的截然不同[12]，因此为了准确地模拟系统响应，需要尽可能精确地刻画流场细节，比如涡，得到流体作用于固体上的力，从而对求解器的高精度以及方法的低耗散有要求。其次，为了适应结构的振动，通常需要网格变形。但当结构振动的幅值很大、或者多个振动物体之间间距很小时，变形网格通常会很扭曲、甚至出现负体积，从而引入过大的几何结构误差，或者直接使得仿真发散。

相对于低阶精度方法而言，高精度方法(三阶及以上)只引入很小的数值耗散。谱方法是最经典的高精度方法之一，在相同的条件下具有最高的精度[15]。但由于谱方法固有的全域性，其应用范围受到了很大限制，难以计算复杂区域的流场。国内学者在谱方法的推进与改良中做出了很大贡献[16-17]。基于网格单元连续的谱差分(Spectral Difference, SD)方法是一种高效的非结构网格高精度算法[18-24]，本文引入了SD方法在三角形/四边形混合网格上对Navier-Stokes方程直接进行空间离散，对复杂流场的适应性非常好。基于SD方法，Zhang等[25-26]提出了滑移网格谱差分(Sliding-mesh Spectral Difference, SSD)方法，用于求解自由转动物体周围的流场，相比于传统的网格协调技术，该方法通过引入滑移界面可以大大减小网格的扭曲程度，从而实现高精度和高效率计算。本文将SSD方法进一步推广，使其可以处理非均匀滑移网格界面，从而减小VIV仿真时网格的扭曲程度，特别是大幅振动或者多个物体振动的情况。最后，研究了并行策略，对求解器进行消息传递接口(Message Passing Interface, MPI)并行，大大提高了仿真效率，增加了求解器的实用性。

1 控制方程

1.1 流体方程

对于流体而言，考虑如下守恒形式的二维非定常Navier-Stokes方程

(1)

式中：Qf为守恒变量；Ff和Gf分别为沿x和y方向的通量，下标f代表流体。为了模拟动网格上的流动，采用任意拉格朗日-欧拉(Arbitrary-Lagrangian-Eulerian, ALE)算法。在此方法中，将真实的时间和空间(t,x(t),y(t))投影到计算空间上(τ,ξ,η)，其中(ξ,η)表示时间无关的计算空间，时间τ=t。由此，Navier-Stokes方程在计算空间中可表示为

(2)

式中：

(3)

其中:|J|为变换雅克比矩阵J的秩；J-1为J的逆矩阵。

1.2 固体振动方程

研究钝体VIV问题所广泛采用的模型是，将一个圆柱弹性连接，置于来流之中，如图1所示。若将振动限制在纵向(比如y向)，则固体的振动就由如下阻尼谐振子方程控制

(4)

式中：m和y分别为固体的质量和纵向位移；c为阻尼系数；k为弹簧的刚度系数；FL为流体作用在固体上的升力(纵向力)。

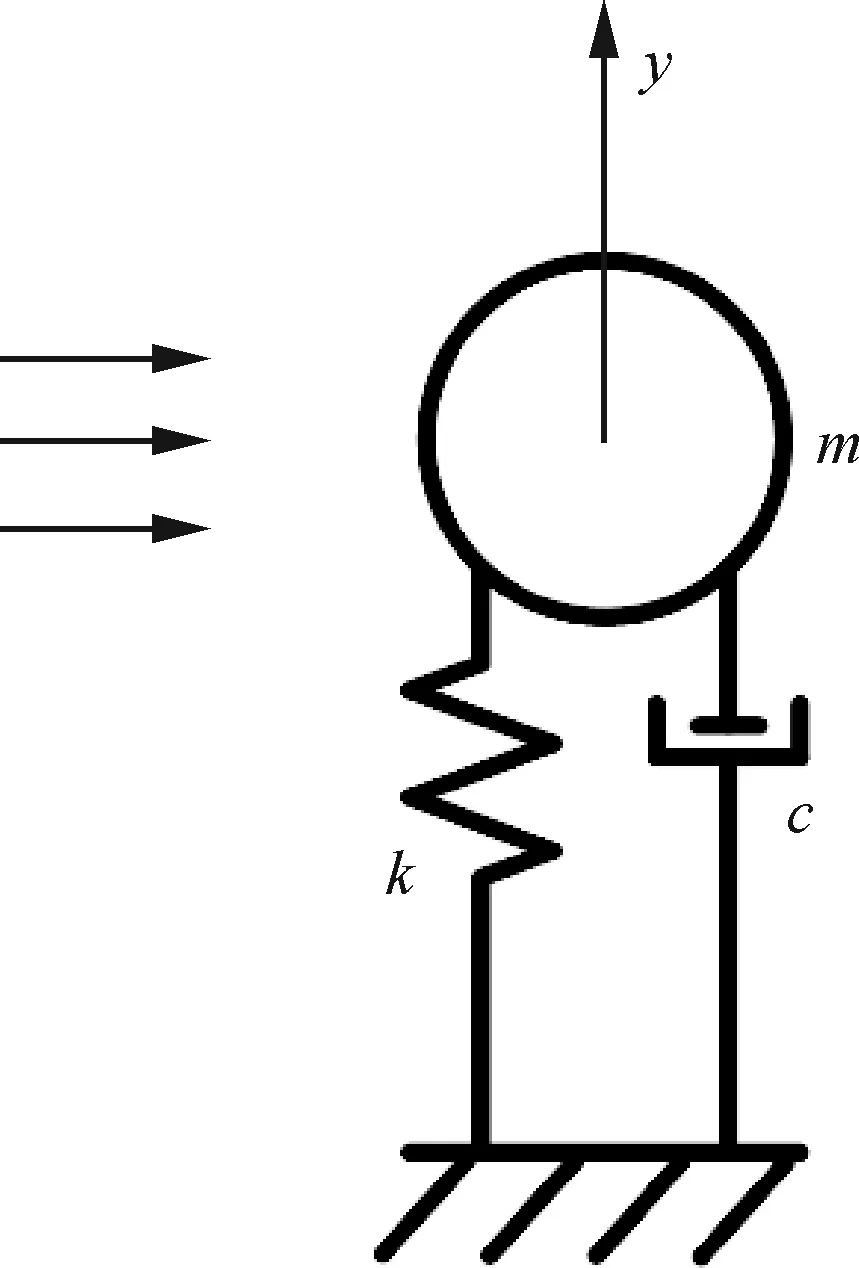
图1 圆柱的质量弹簧阻尼系统示意图Fig.1 Diagram of a mass-spring-damper system for a circular cylinder

1.3 流固耦合方程

为了耦合固体方程和流体方程(对时间具有一阶导数)，需要将式(4)变换为两个时间一阶导的方程组

(5)

式(5)进一步可以写成如下残差形式

(6)

式中：

(7)

(8)

Qs和Rs分别为固体的自变量和残差的向量,下标s代表固体。

类似地，将流体方程也写成如下的残差形式

(9)

式中：

(10)

(11)

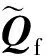
联立式(6)和式(9)可得到全耦合的守恒系统

(12)

式中：

(13)

Q和R(Q)分别为耦合的自变量和残差的向量。VIV数值模拟中，将对式(12)进行时间推进。

2 数值方法

2.1 高阶网格下的SD方法

对流体方程进行空间离散首先要通过式(14)的映射方程，将物理空间内的动网格单元映射到计算空间的静止网格单元上

(14)

式中：(x,y)表示物理空间；(ξ,η)表示计算空间；K为一个网格单元的节点数；(xi,yi)为随时间变化的第i个节点坐标；Mi为和节点对应的形函数。

图2显示了用不同精度的网格单元去拟合真实物理单元的情况。比如，对于一个二阶三角形和四边形网格单元，K=6,8。显然，相比于低精度网格，高精度曲边网格能够把具有曲面(边)几何形状的物体拟合得更精确。基于这个原因，本文中所有曲线边界都用三阶精度网格进行拟合。

SD方法通过在网格单元内部分布的解点(Solution Points，SPs)与通量点(Flux Points，FPs)来构造单元内连续的解多项式和通量多项式。关于SD方法在三角形/四边形混合网格上解点与通量点分布的详细描述，可参考文献[27]。

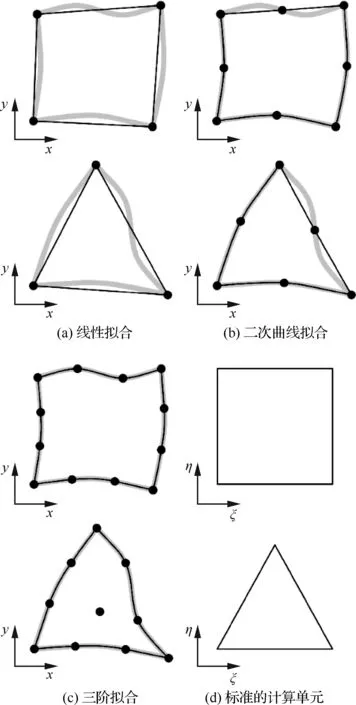
图2 不同阶数的网格单元(细黑线)与真实的物理单元(粗灰线)Fig.2 Grid elements (thin black lines) in different orders for approximating curved physical cells (thick gray lines)

对于三阶精度SD格式而言，三角形和四边形单元上的解点与通量点分布如图3所示，灰色箭头表示通量点处的自由度方向。

由于SD方法所构造的解多项式和通量多项式只在网格单元内部连续，在网格单元边界处是间断的。为了保证方法的守恒以及稳定，本文采用Rusanov黎曼求解器[28]在单元边界处计算相邻网格之间的共同无黏通量。

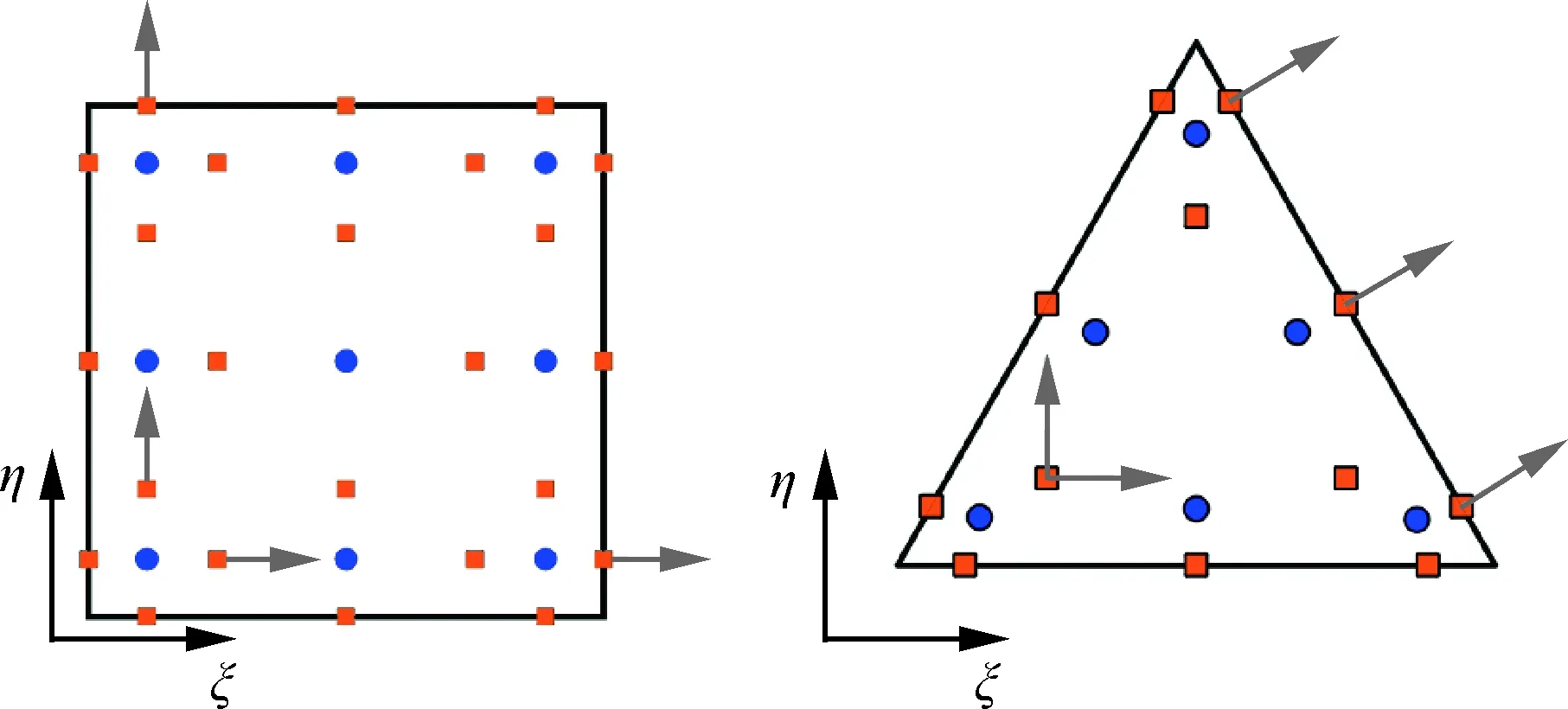
图3 三阶SD格式四边形和三角形单元上的解点(蓝色圆圈)和通量点(橘色方块)分布示意图Fig.3 Schematic of distribution of solution points (blue circles) and flux points (orange squares) for a third-order SD scheme on a quadrilateral element and a triangular element

2.2 动网格策略

对于VIV而言，当固体结构位置变化时，流场区域也随之改变。本文将调配函数[29]与滑移网格相结合，使之适用于极端情况的网格变形问题。

以图4中单个纵向振动圆柱的例子，详细解释一下该方法。通过两个滑移界面，将整个流场区域分为3个子区域。两边的两个子区域是静止的，中间的区域可以变形以适应圆柱的运动。中间的区域进一步以距圆心d1和d2为界,分为3个虚拟的区域：在区域Ⅰ中，网格是刚性的，随着圆柱一起运动；区域Ⅱ中，网格可以变形；区域Ⅲ中，网格保持静止。

图5用两个振动圆柱网格变形的例子来说明滑移网格方法的优势。图5(a)是初始网格，两个圆柱相隔两倍直径放置。图5(b)是当两个圆柱在纵向相对运动了一个直径的距离时，用连续协调变形方法得到的网格。显然，网格在第1个圆柱的上方和第2个圆柱的下方变得非常扭曲。图5(c)显示了滑移网格方法的结果，充分说明了通过引入滑移界面，可以很大程度地提高网格质量。

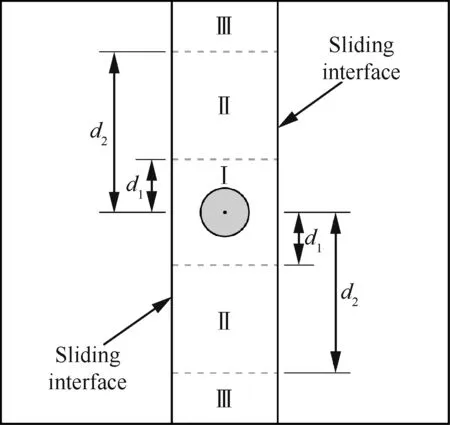
图4 用两个滑移界面将单个振动圆柱计算域分割的示意图Fig.4 Schematic of a computational domain with two sliding interfaces for a vibrating cylinder

图5 围绕两个振动圆柱的网格变形示意图Fig.5 Schematic of meshes deformation for two vibrating cylinders

理想情况下，网格运动不应该污染流场。最简单的情况便是：动网格下定常自由来流应能始终保持定常，称之为自由流保持(Free-stream Preservation)。为了满足自由流保持，将自由来流参数代入式(2)，经过变换，可以得到如下方程组：

(15)

式中:ξx、ξy、ξt、ηx、ηy和ηt均为变换雅克比矩阵J的元素。

式(15)只与网格的几何变量相关，与流场参数无关，所以通常称之为几何守恒律(Geometric Conservation Law, GCL)[30]。对式(15)方程组进行积分处理后会发现：前2个方程的物理意义是一个闭合的单元且必须一直保持闭合；第3个方程的物理意义是物理空间的体积变化率等于其边界扩展的速度。

对于GCL的处理，国内外学者已经做了很多研究[31-35]。由映射关系式(14)可知，和空间变换相关的量(|J|ξx等)可以表示成拉格朗日插值多项式形式，而SD格式中空间离散是对变量直接进行微分，因此，若构造曲线网格的多项式阶数不高于构造守恒变量的多项式阶数，式(15)中的前两个等式能够自动满足[31,35]。但SD格式中时间推进并不是解析的，导致式(15)中第3个方程并不能自动满足。一种可行的做法是将|J|视为未知量，采用和流场方程相同的时间及空间离散格式进行更新，取代由网格坐标直接计算得到|J|的做法[33]。

在SD方法中的具体计算过程为：将GCL第3个方程写成如下形式:

(16)

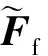
2.3 滑移网格分块

并行计算首先要将全部网格分配给各个处理器，由于计算网格已经被滑移界面分成了几个子区域，因此并行时网格的分块策略值得详细研究。假设一共有NP个处理器，滑移界面将网格分为NM个子区域，将子区域合起来视为一个大的区域，在这个单独但间断的区域上进行网格分块。步骤如下：

步骤1根处理器读入NM个子区域的网格信息并存储。

步骤2通过加上相应的偏移量，根处理器将各个子区域上的网格单元、节点以及边界等的编号转成全局编号。偏移量是之前子区域上相应项目数量之和。例如，对于一个具有3个子区域的问题而言，若每个子区域上的网格单元数量都是100，那么子区域1、2和3的网格单元偏移量分别是0、100和200。

步骤3根处理器调用Metis库[36]里的函数，将整个大区域上的网格分成NP块。

步骤4根处理器将分块信息播散给其他子处理器。

步骤5所有处理器根据分块文件读入各自块的网格信息。

这种方法的优势是其实际的分块数量通常是最小的，减少了处理器之间的信息传递。另外，可以实现全局的负载平衡。比如图6是6个处理器时图5(c)对应网格的分块情况，其中粗黑线表示分块边界。从图中可以看出，P0和P5的分块都不连续，分别在两个子区域上，但对于全局而言实现了负载平衡。实际上，对于网格量很大的情况(相对于处理器数量而言)，分区通常都是连续的，因此这种方法在达到负载平衡的同时也能使分块数量最小。

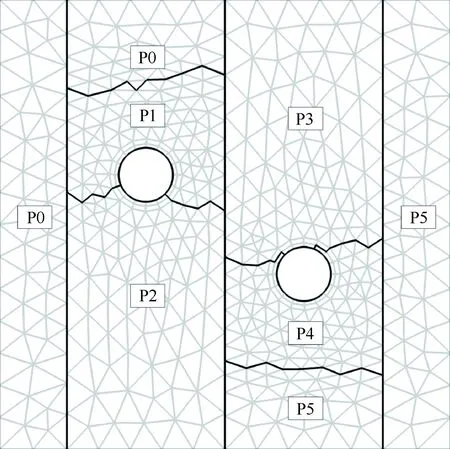
图6 6个处理器对绕两个振动圆柱网格的分块示意图Fig.6 Schematic of partitions of a mesh around two vibrating cylinders via 6 processors

2.4 滑移界面通信

滑移界面两侧的网格不均匀而且网格点有错位，导致了两侧网格实际上是间断的，本文采用粘接元方法进行滑移界面两侧的信息传递[37]。粘接元方法的主要思想是：将解/通量从网格面Ω投影到粘接元Ξ(如图7(a))，计算得粘接元上的解/通量后，将数据投影回网格面(如图7(b))，以保证流场的守恒。滑移界面处，每一个网格面对应一个或者多个粘接元，而每一个粘接元左右各对应一个网格面。在时间推进的每一步都需要更新这种网格面-粘接元的对应关系。

图8(a)为串行求解器中两块滑移网格之间的粘接元分布示意图，影线部分表示粘接元。对于并行求解器而言，情况有所差别。图8(b)显示了5个处理器时两块滑移网格之间的粘接元分布，其中黑色影线部分表示当地粘接元，灰色阴影部分表示全局粘接元。每个处理器都对应有当地粘接元，且每个粘接元只和一个网格面相对应。如图8(b)中处理器P1上的当地粘接元只和其左侧的网格面对应，因此左侧的解/通量可以从当地直接获得，而右侧的解/通量则需要从处理器P3或P4其上对应粘接元发出。对于其他处理器上的粘接元也类似。通过当地-全局粘接元对应关系，当地粘接元可以找到其在其他处理器上对应的粘接元。

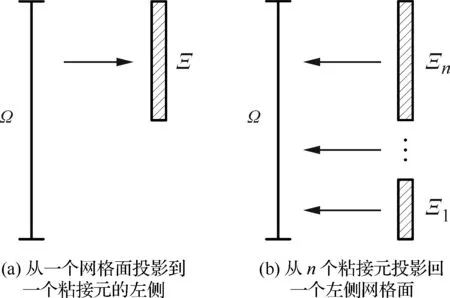
图7 网格面和粘接元之间的投影关系Fig.7 Projection between a cell face and mortars

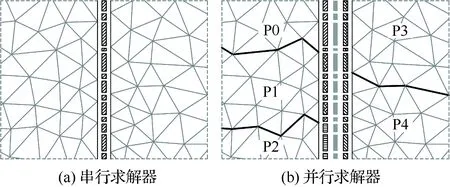
图8 两块滑移网格之间的粘接元分布示意图Fig.8 Schematic of distribution of mortars between two sub-domain meshes with relative sliding motion

为了保证处理器之间信息传递的正确，网格面-粘接元对应关系以及当地-全局粘接元对应关系需要在每一迭代步更新。由于滑移界面处的网格节点数是固定的、在仿真过程中总粘接元数量也保持不变，因此，为了加快速度，可以用两个处理器分别从同一个滑移界面的两端开始更新网格面-粘接元以及当地-全局粘接元对应关系。

3 数值算例

本节验证非均匀滑移网格方法对无黏和有黏流动的空间精度，并证明高阶精度格式的低耗散特性，随之，模拟4个圆柱的VIV算例来验证并行求解器的加速效果。算例采用5步4阶显式龙格-库塔格式进行时间推进[38]。所有算例都是在无量纲化后进行计算的。

3.1 Euler vortex流动

在Euler vortex流动[39]中，均匀来流输运一个等熵涡。Euler vortex流动在无穷大区域内的解析解为

(17)

式中：u、v、ρ和p分别为Euler vortex流动中x和y方向的速度、密度和压力；U∞、ρ∞、p∞和Ma∞分别为均匀流的速度、密度、压力和马赫数；γ为比热比，通常取为1.4；θ为均匀流方向；ε和rc分别为涡的强度和尺寸；相对坐标(xr,yr)的定义为

(18)

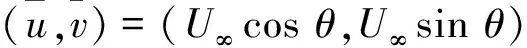
在本仿真中，均匀来流的流动参数是：(U∞,ρ∞)=(1,1)，马赫数Ma∞=0.3，涡随均匀流沿θ=π/6方向运动。计算域为0≤x≤10,0≤y≤10。仿真初始时刻，将强度和尺寸分别为ε=1和rc=1的涡置于计算域中心，即(x0,y0)=(5,5)。在x=3和x=7两处将计算域分为3部分。两侧的子区域用三角形单元划分，中间用四边形单元划分。用网格量分别为44/15、156/50、568/200和2 216/800的4套三角形/四边形混合网格进行精度测试。令中间子区域的水平中线(y=5，3≤x≤7)以方程Δy=sin(0.5t)随时间运动，变形区域限定为|y-5|≤4。两侧子区域网格则保持静止。

图9显示了在568/200混合网格上用8个处理器并行求解四阶精度格式得到的流场密度云图，图9(a)对应初始时刻，图9(b)为无量纲时间t=2.3时刻涡心刚好运动到滑移界面时的情况，图9中浅灰色为网格线，深灰色为处理器边界。可以看出，涡的层次清晰，滑移界面完全不会污染流场。

通过密度的L1和L2误差，进一步验证了计算精度。两个误差定义为

(19)

(20)

(21)

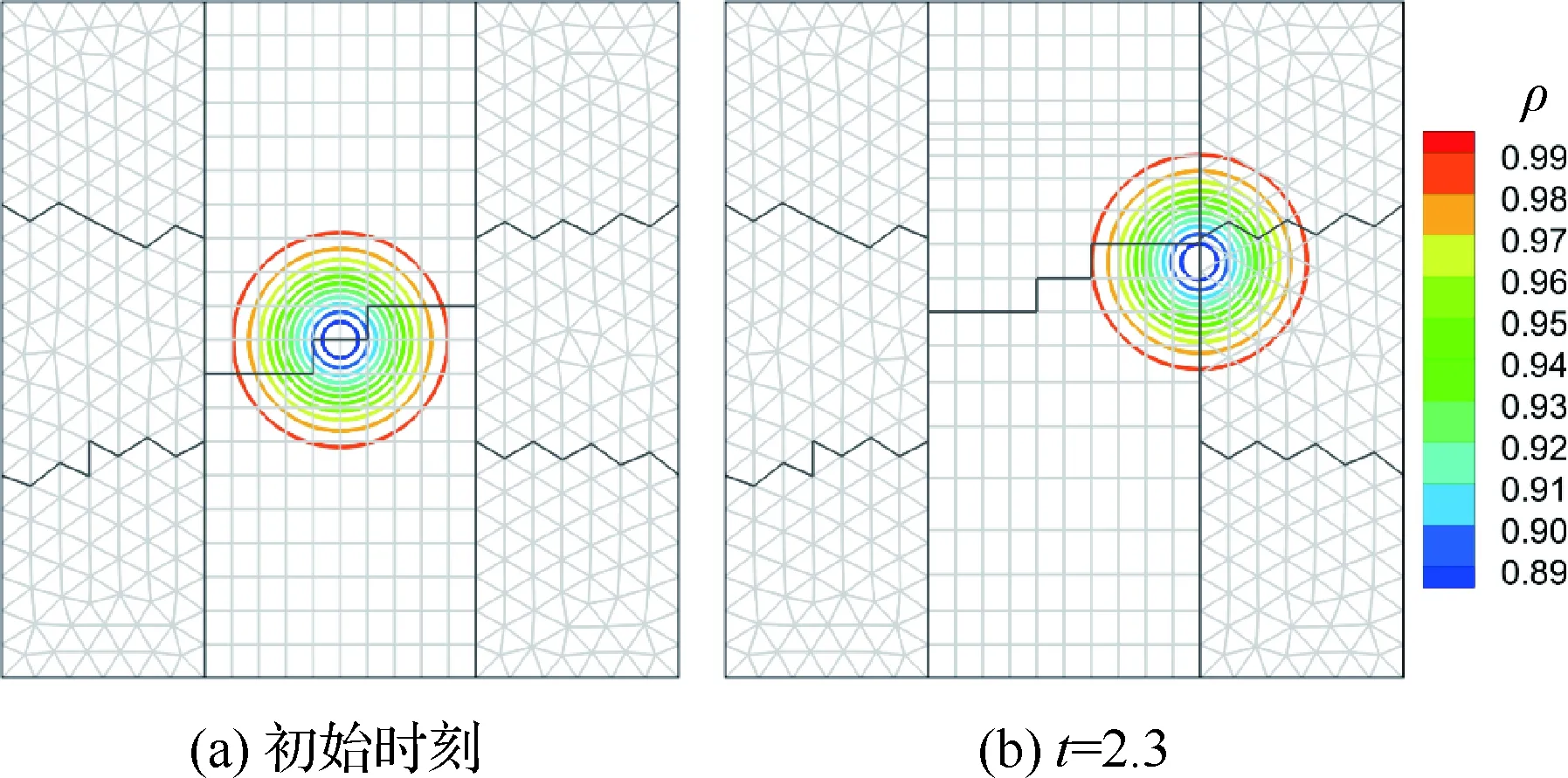
图9 Euler vortex流动对应的密度云图Fig.9 Density contours for Euler vortex flow

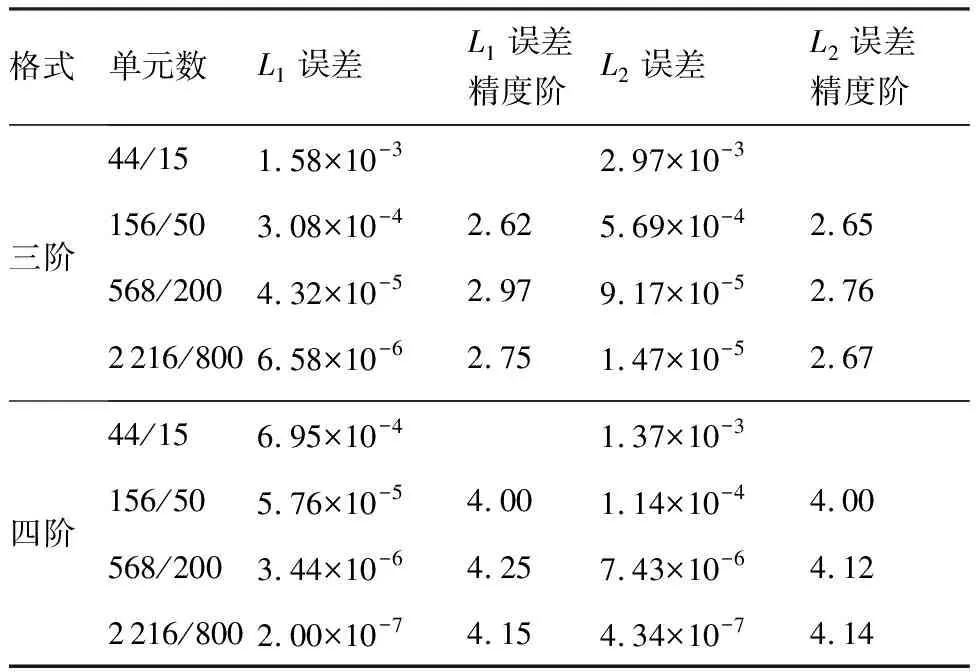
表1给出了t=2.3时刻上述4套网格在三阶和四阶格式下的误差和精度。精度的计算依据为

(22)

式中：order为精度阶；error为误差值；下标coarse和fine分别表示粗网格和密网格。

从表1中可见，误差随着网格的加密逐渐减小。当使用三阶精度格式时，数值计算得到的精度阶数略小于3；四阶精度格式得到的结果略大于4。很明显，尽管存在不连续的滑移界面，滑移网格方法还是能够在无黏流动中保持SD方法的高精度。

表1Eulervortex流动仿真的误差和精度的阶数(基于密度计算)

Table1Errorsandordersofaccuracy(basedondensity)forEulervortexflowsimulation

格式单元数L1误差L1误差精度阶L2误差L2误差精度阶三阶44/151.58×10-32.97×10-3156/503.08×10-42.625.69×10-42.65568/2004.32×10-52.979.17×10-52.762216/8006.58×10-62.751.47×10-52.67四阶44/156.95×10-41.37×10-3156/505.76×10-54.001.14×10-44.00568/2003.44×10-64.257.43×10-64.122216/8002.00×10-74.154.34×10-74.14

3.2 平板Couette流动

对于在两个相距H的无限长平板之间的黏性平板Couette流，如果上板的温度是Tt且以速度U运动，下板温度为Tb且静止，那么稳态流场为

(23)

式中：e=cVT为内能,cV=R/(γ-1)为定容比热容,T为温度，R为气体常数；下标b和t分别表示下板和上板；Pr为普朗特数，本文取为0.72。

在本算例中，设H=1，U=1.0，Tb=Tt=1.0。上板处的马赫数Mat=0.1。雷诺数的值依赖于H、U以及流体黏性(假设为常量)，取为Re=100。计算域为0≤x≤2和0≤y≤H，并被x=0.6和x=0.4两条直线分为3个子区域。令中间子区域的水平方向的中线以Δy=0.1sin(0.5t)运动，且其网格变形区域限制在0.1≤y≤0.9之间。剩余两个子区域网格保持静止。上下采用无滑移恒温壁面边界条件，左右视为周期性边界条件。测试中用到了3套网格，分别含有4/4、16/16和64/64个三角形/四边形混合网格单元。

图10显示了在64/64混合网格上用四阶精度格式仿真得到的稳态平板Couette流马赫数(Ma)云图,图中浅灰色线为网格线，深灰色线为处理器界面。很明显，网格的运动以及滑移界面网格的错位并没有引入任何可见的扰动。马赫数云图在纵向层次分明，且沿水平方向保持不变，与流场解析解一致。

误差和精度的计算方法与Euler vortex流中一致，表2显示了用速度u算得的结果。同样地，随着网格密度的增加，L1和L2误差都相应地逐渐减小，精度也在3和4左右。因此，对于黏性流动而言，该滑移网格方法依然可以达到理想的精度。

为了便于说明高精度求解器的低耗散特性，将图10所示的流场区域全部用四边形单元进行划分，中间子区域网格的运动规律保持不变。采用二阶精度格式分别在单元数为200和800的两套网格上进行仿真，四阶精度格式在单元数为50和200的两套上进行仿真，从而两种精度格式两次仿真的自由度分别都为800和3 200。图11显示了4次仿真密度的L1误差随迭代步数的变化曲线。由图可知，在相同自由度的情况下，四阶精度格式误差始终小于二阶精度格式；甚至自由度为800的四阶精度格式仿真误差也明显小于自由度为3 200的二阶精度格式仿真误差，验证了高阶精度格式的低耗散性。

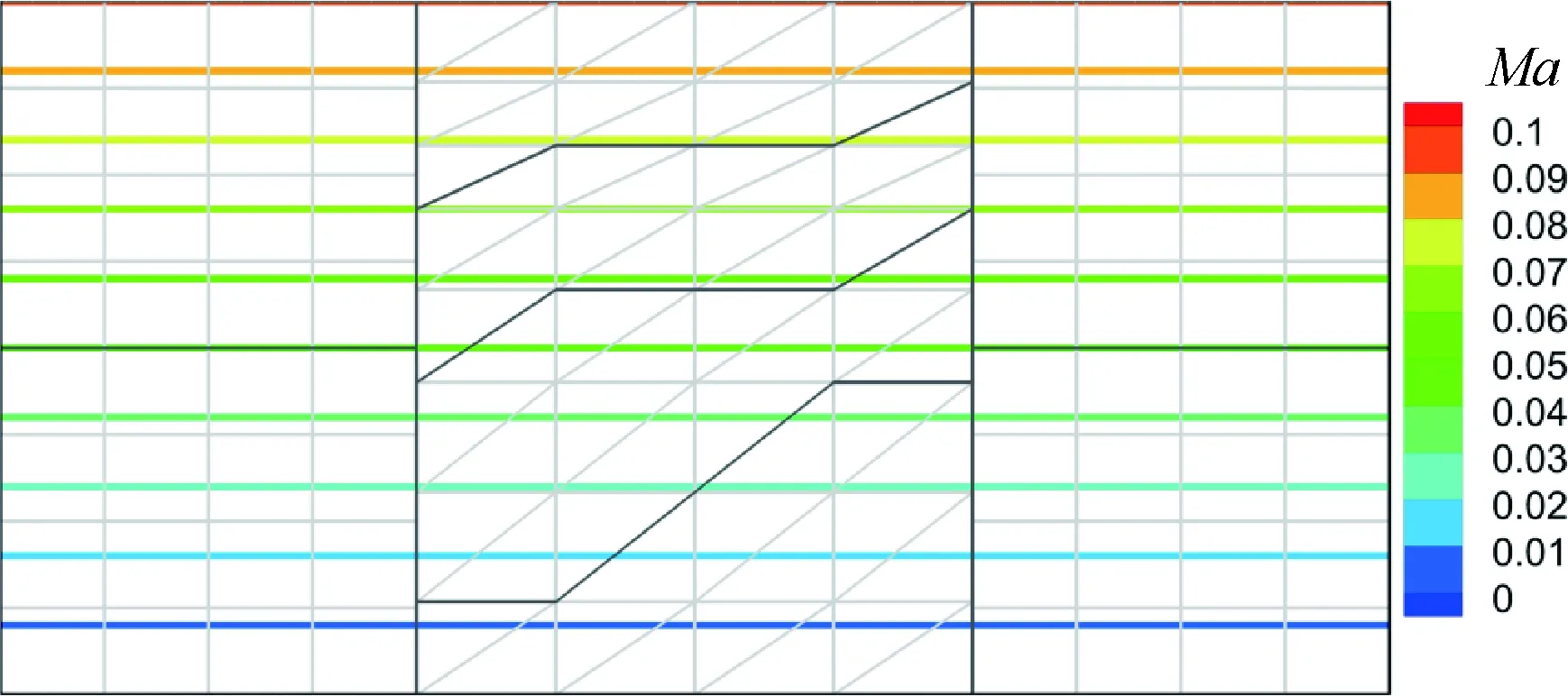
图10 平板Couette流马赫数云图Fig.10 Mach number contours for planar Couette flow

表2平板Couette流动仿真的误差和精度的阶数(基于速度u计算)

Table2Errorsandordersofaccuracy(basedonuvelocity)forplanarCouetteflowsimulation

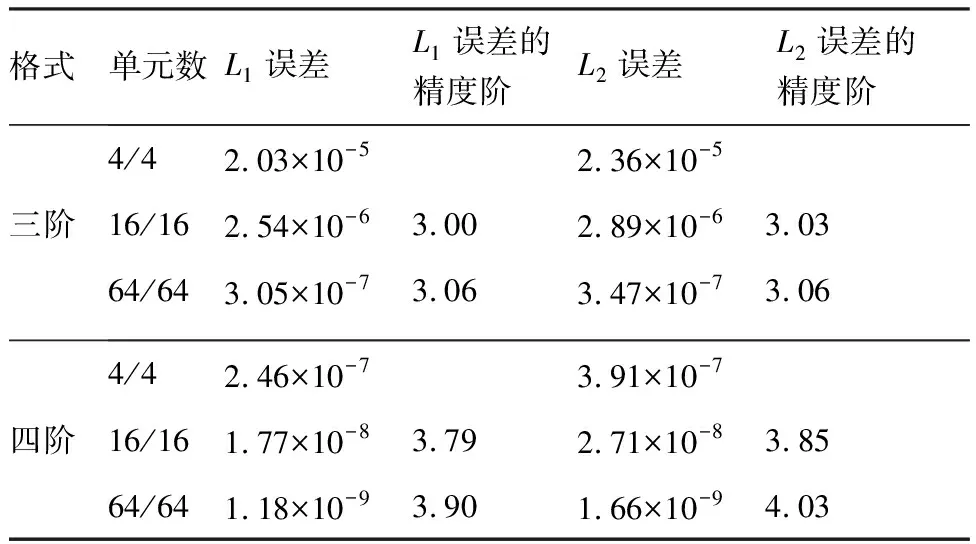
格式单元数L1误差L1误差的精度阶L2误差L2误差的精度阶三阶4/42.03×10-52.36×10-516/162.54×10-63.002.89×10-63.0364/643.05×10-73.063.47×10-73.06四阶4/42.46×10-73.91×10-716/161.77×10-83.792.71×10-83.8564/641.18×10-93.901.66×10-94.03

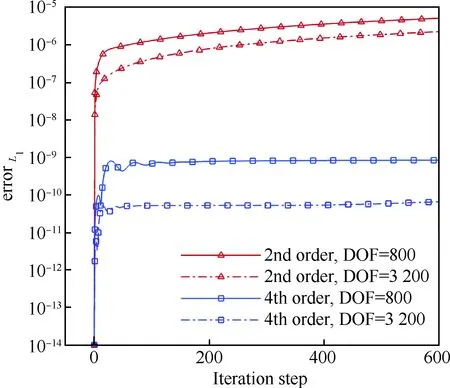
图11 平板Couette流动仿真密度的L1误差随迭代步数变化Fig.11 Variation of L1 errors of density with iteration steps for planar Couette flow simulation

3.3 定常均匀来流数值模拟

如图12(a),计算区域为10×10的矩形，划分为三角形和四边形混合网格，上下左右都设为周期性边界条件。两条黑色的滑移界面将流场分为3部分：中间子区域的水平中线(y=5，3≤x≤7)以方程Δy=sin(0.5t)随时间运动，则周期T=4π,上下两侧区域相应地拉伸或压缩，变形区域限定为|y-5|≤4；左右两侧子区域内部网格点按式(24)所示规律运动(其中，IV为网格点的序号)。图12显示了仿真初始时刻和仿真过程中两个不同时刻的网格情况，其中图12(a)为初始时刻网格。

(24)

流场初始化为均匀来流，马赫数取0.3。采用四阶精度格式离散Euler方程，时间步长取为1.0×10-3。图13给出了满足GCL(|J|作为未知量在时间推进中迭代更新)和不满足(|J|由网格坐标信息直接算得)情况下，密度的L1和L2误差对比。从图中可以看出，在网格有压缩和扭曲的情况下，满足GCL的自由流仿真算例能够维持在机器零附近没有增加，证明了求解器的自由流保持特性。

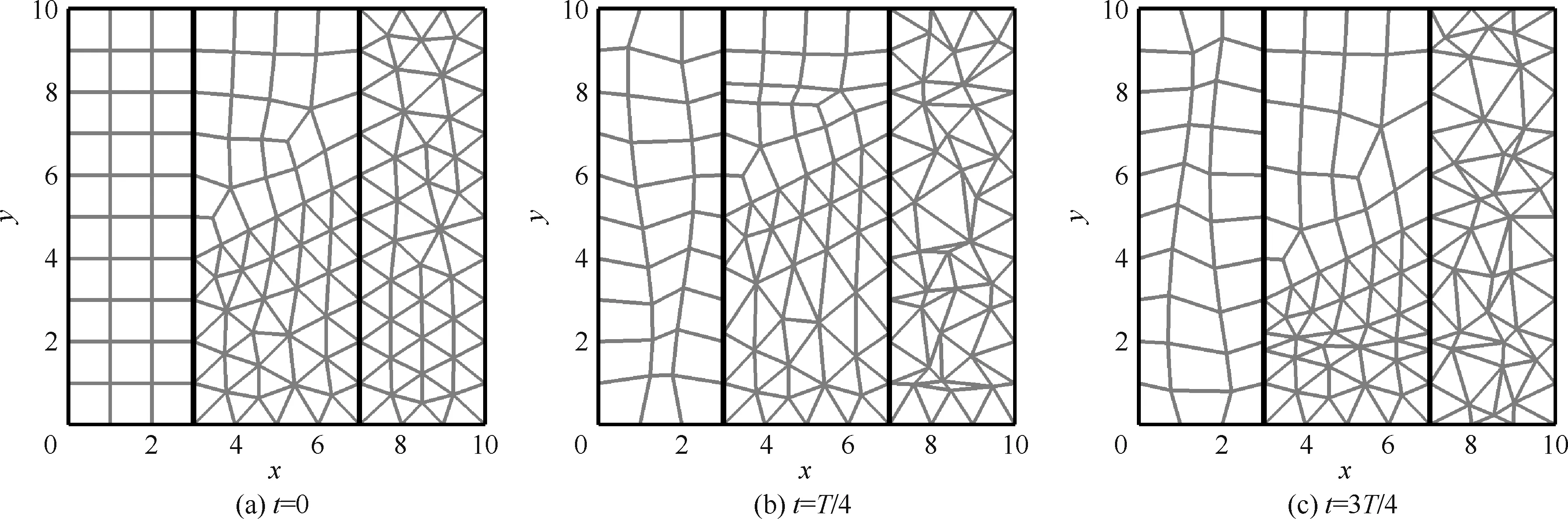
图12 3个不同时刻对应的流场网格Fig.12 Meshes of flow field at three different time instants

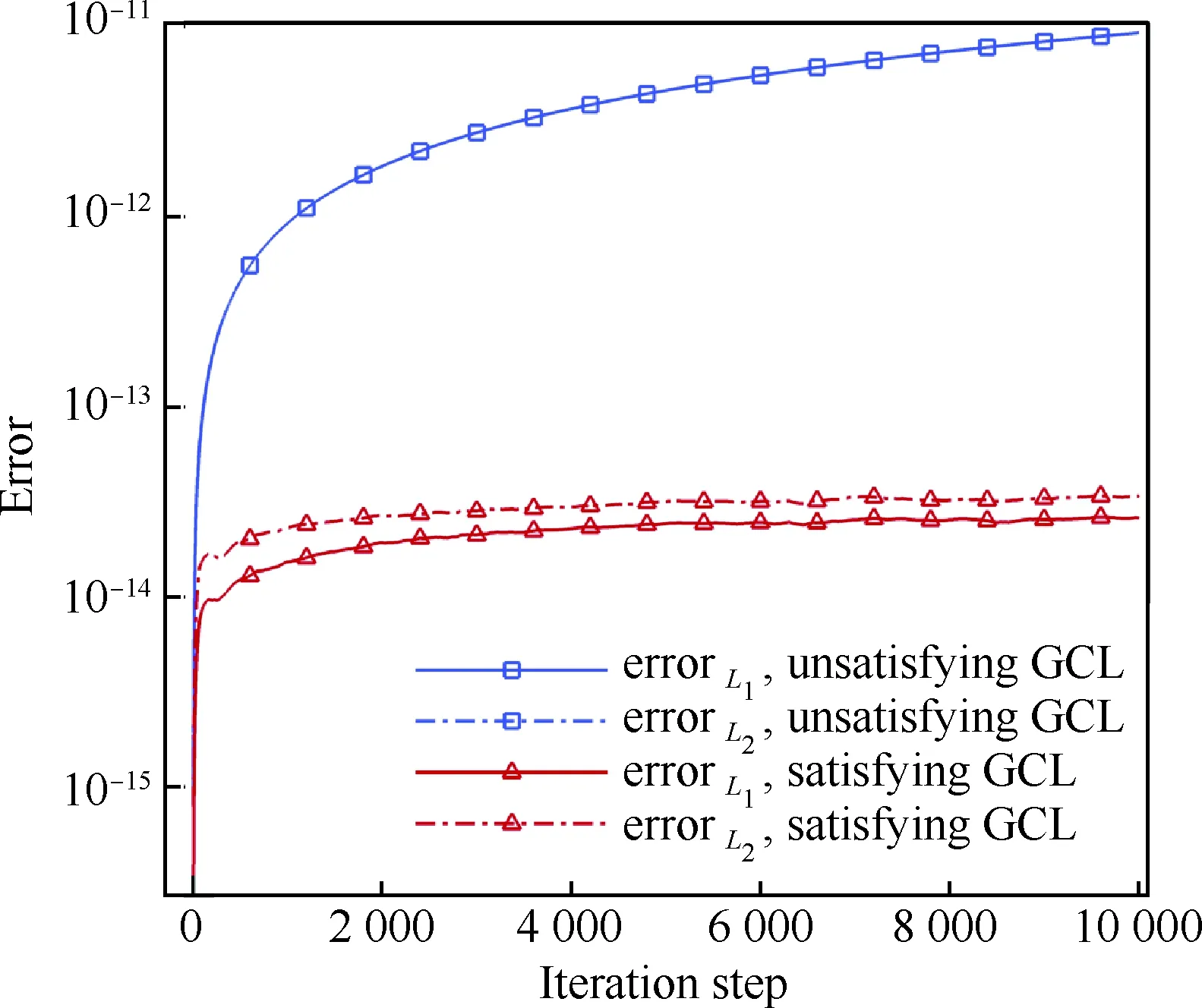
图13 四阶精度格式自由来流仿真密度误差变化Fig.13 Density error history of 4th order scheme for free stream flow simulation

3.4 单个圆柱的VIV数值模拟

此算例对弹性连接的单个圆柱进行VIV仿真，并与其他文献中的结果进行比较，验证方法的有效性。计算状态为：自由来流马赫数Ma∞=0.2，雷诺数Re=100，圆柱的质量比为m*=10.0，速度比U*=4.92，阻尼比ζ=0(变量定义见文献[12])。

圆柱直径D=1，计算区域长与宽为60D×20D，圆柱圆心距入流边界10D，两个滑移界面将流场分为3个子区域。流场划分成6 696个混合网格单元，圆柱周边和尾迹区网格进行了加密。边界条件设置为：狄利克雷入口边界条件、压力出口边界条件、上下为对称边界条件、圆柱表面为无滑移绝热壁面。时间推进步长为Δt=5.0×10-4。圆柱沿来流方向(x方向)和垂直来流方向(y方向)都可以振动，x方向振动的控制方程也为式(4)，控制参数和y方向参数一致。因幅值很小，单纯的解析变形函数便可满足x方向的变形要求。

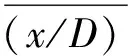
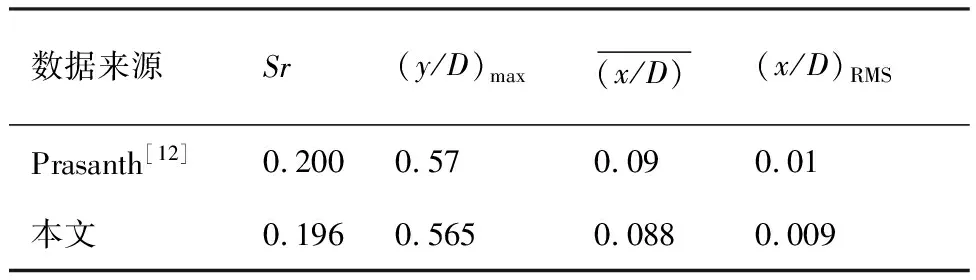
表3 单个圆柱VIV数值模拟响应Table 3 Response of single cylinder VIV simulation

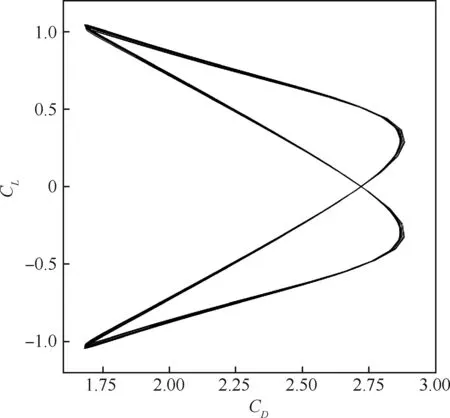
图14 t从220到600过程中单个圆柱仿真CL和CD的利萨茹曲线Fig.14 Lissajous curve of CL and CD for single cylinder from t=220 to t=600

3.5 一列4个圆柱的VIV数值模拟

此算例对置于一列的4个圆柱进行VIV仿真，目的是测试求解器的加速效果，并且验证求解器处理流场中存在多个物体，相互之间具有较大相对运动情况的能力。相邻的两个圆柱间隔ΔL/D=1.0，自由来流马赫数Ma∞=0.1，雷诺数Re=200，每一个圆柱的质量比都为m*=5.0，速度比U*=9，阻尼比ζ=0。

计算域的范围为74D×50D，前面的圆柱距离入流边界20D，用5个滑移界面将流场分为6个子区域。流场一共划分为58 436个混合网格单元，其中中间4个动网格区域分别有7 116个单元，前面的静止网格区域有8 708个单元，最后的静止网格区域有21 262个单元，对圆柱周边和尾迹区网格进行了加密。边界条件设置为：狄利克雷入口边界条件、压力出口边界条件、上下为对称边界条件、圆柱表面是无滑移绝热壁面。时间推进步长为Δt=2.0×10-4。

图15显示了一定时间内段内4个圆柱的位移随时间变化曲线。由于流场的涡结构比较复杂(见图16)，所以圆柱的位移响应也比较丰富。平均振幅的相对大小在0.6～1.0之间，相对于圆柱间隔而言是比较大的。图16是某一时刻流场的涡量云图，灰线表示处理器的分区界面，水平的点画线表示4个圆柱初始所在的位置。从图中可以看出求解器能够很清晰地刻画流场，证明了本文动网格方法的可靠性。

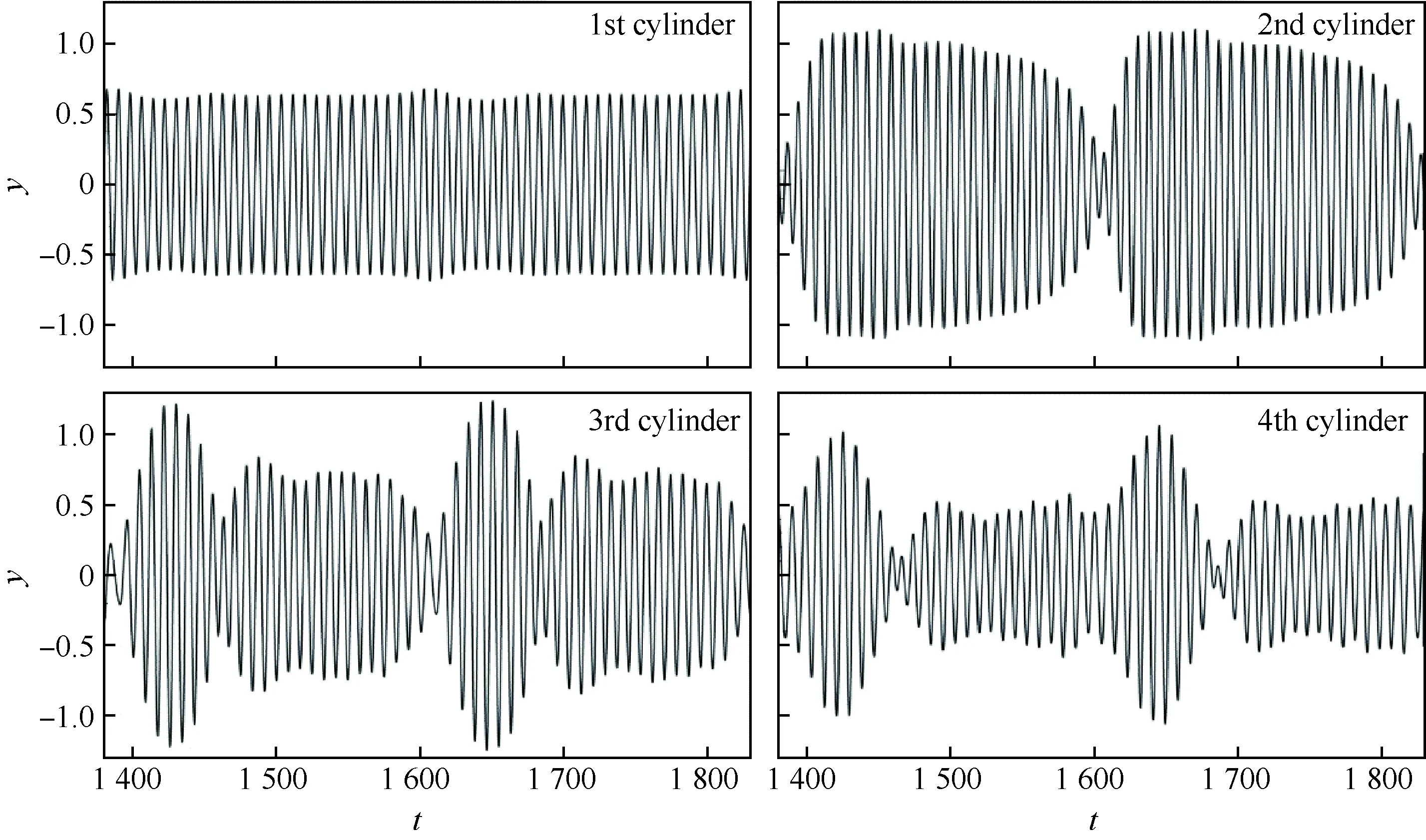
图15 4个圆柱的位移随时间变化曲线Fig.15 Displacement history of four cylinders

测试并行求解器加速效果时用到了多达240个处理器，图17显示了加速效率(Speedup)随所用处理器数量(Number of processors)的变化关系，其中Linear表示理想情况下所能达到的线性加速效果。对于具有NM-1个滑移界面的网格，最多可以有2(NM-1)个处理器去更新滑移界面处的网格面-粘接元对应关系以及当地-全局粘接元对应关系，剩余的处理器需要等待，造成了一点资源浪费。由图17可见，在120个处理器以内，加速基本都能保持线性。随着处理器数量的继续增加，处理器之间的信息传递时间以及更新粘接元对应关系的等待时间占总时间的比重也在增加，影响了加速效果。

同时，对比3条加速曲线可以发现，精度越高，加速效果越好。因为随着精度增加，处理器内部需要处理的自由度以O(N2)增加，而边界交互自由度只以O(N)增加，使得处理器之间信息传递以及等待时间所占比重也相对减小。同理，对网格进行加密时，也会使得线性加速的效果能够保持到处理器数量更大的时候。因此该求解器适用于进行大规模并行仿真。

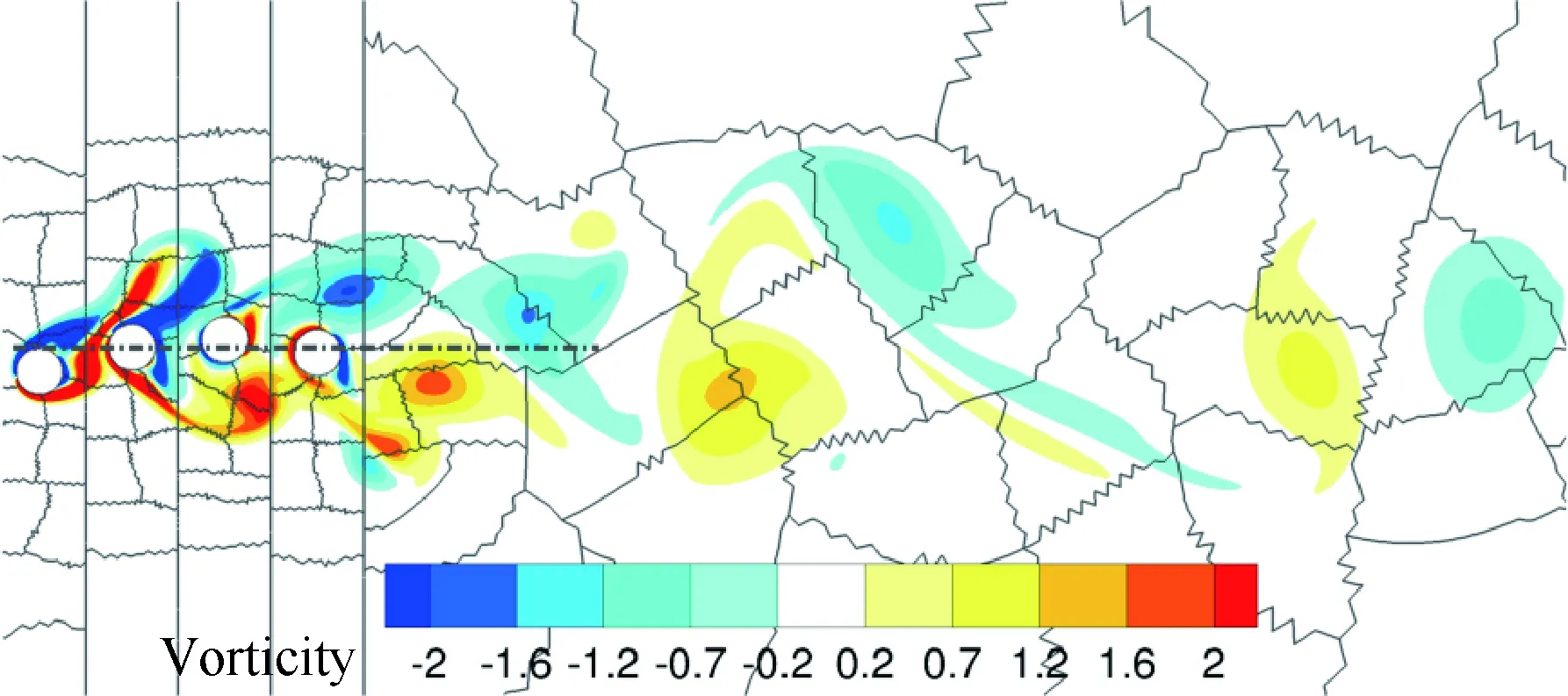
图16 某一时刻流过4个涡激振荡圆柱流场的涡量云图Fig.16 Vorticity contours at one instant for a row of four vibrating cylinders

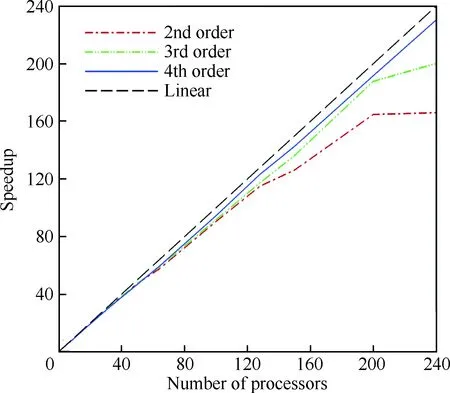
图17 并行求解器加速曲线Fig.17 Speedup curves of parallel solver

4 结 论

1) 提出了一种适用于涡激振荡仿真的并行高精度方法，可用于研究大振幅、小间距等极端VIV问题。

2) SD方法在三角形/四边形非结构混合网格的应用，使得求解器对于复杂外形处理能力增强；利用了非均匀滑移网格方法，克服传统协调网格方法所受到的变形幅度的限制，可以方便地实现网格变形，保证良好的网格质量，并满足GCL条件。

3) 数值算例表明，该方法对于无黏流动和黏性流动都能保持原SD方法的高阶精度，证明了求解器具有低耗散性的特性，能够精确捕捉流场细节，从而使得VIV仿真准确。

4) 并行测试证明该求解器具有较好的加速效果，且所用数值格式精度越高、网格数量越大，加速效果越好，因此该求解器适合于大规模并行计算。