考虑间隙和拧紧力矩的复合材料钉载分配均匀化方法

李鹏，周晚林,*，李蓓，邵金涛

1. 南京航空航天大学 机电学院，南京 210016 2. 南京林业大学 经济管理学院，南京 210037

多钉单剪连接已广泛应用于飞机复材结构，但各螺栓的承载载荷有着较明显的差异。由于碳纤维复合材料是各项异性材料且不存在明显的塑性区，故多钉连接结构中几乎不具备载荷重新分配的能力，造成随着外载荷的增加，各钉承载比例几乎不变。国内外学者对钉载分配的计算和测量以及载荷均匀化做了大量研究。

目前，确定复材多钉连接钉载比例的方法主要有：解析模型预测法(如经典刚度法[1]和弹簧质量法[2-3]等)、有限元分析方法[4-8]和试验测定法[9-12]等。其中，试验测定法由于试验结果的可靠性在实际结构分析中得到广泛应用。试验测定的一般方法有：采用压力传感器[9-10]测量钉-孔的接触压力、使用带传感器螺栓[12]直接测量钉载以及采用表面应变计测量旁路载荷[10-11]。对于单剪螺栓连接的双板结构，由于结构不对称导致偏心弯曲，使得通过测量表面应变经数据处理得到的旁路载荷比例存在较大误差。为了解决这一问题，国内有学者采用防弯夹具约束[10]进行测试，但是由于防弯夹具改变了多钉单剪连接的受力情况，则与实际结构承载情况不符。本文采用测量弯曲导致应变对旁路载荷应变进行修正的方法，对多钉单剪连接进行试验测试，结果较为准确。

在钉载分配优化研究中，由于复材连接结构在设计时只有挤压失效是被允许的[1]，为避免多钉连接中某一钉出现较高的承载导致灾难性的失效，应尽可能确保结构在荷载作用下多钉载荷的分配达到均匀化。Watkins和Jakiela[13]在非线性有限元中采用遗传算法对螺栓布局进行了优化。邵祝涛[14]采用枚举法对层合板多排多列机械连接结构排列的布局进行了优化。Yun等[15]采用有限元的方法，在多钉双剪连接的各个螺栓上逐个施加单钉双剪连接的失效载荷，分别求解各个螺栓的相对位移，然后以求解位移作为各钉孔设计间隙，以此，接头承载能力提高了13.1%～21.8%。Mandal和Chakrabarti[16]采用三维有限元的方法，提出建立一种等效的均匀三维弹性模型来简化复合材料多钉连接载荷均匀化问题。谢宗蕻等[17]基于弹簧质量模型，以钉-孔间隙为设计变量进行了钉载分配比例优化，通过有限元分析验证效果较好。目前，钉载分配优化比较通用的技术方法是：结合神经网络和遗传算法的有限元分析技术，但是，该方法计算量大且优化过程复杂，在工程设计中具有一定的局限性。

钉载分配的影响因素很多[2,11-12,18-19]，但考虑航空中的安全与减重、钉-孔间隙和拧紧力矩对钉载分配的影响相对容易实现且效果较为明显。钉-孔间隙对降低首、尾排钉承载比例的效果较好，但飞机装配中，钉-孔间隙不超过钉孔直径的1%[20-21]。拧紧力矩对钉载分配有较大影响[2,12]，但是飞机装配中对拧紧力矩有较严格的推荐值范围[1]。本文基于改进的应变测量法测量钉载分配比例，以钉-孔间隙和拧紧力矩为设计变量，建立一种较为简便的多钉连接钉载分配线性优化模型，采用单纯形算法对模型进行求解，从而得到优化后的配合间隙和拧紧力矩。

1 改进的应变计测量法

1.1 试验件参数

试验采用T700/FRD-YG-40S碳纤维增强环氧树脂基复合材料层压板，其力学性能见表1，铺层顺序为[45/-45/0/45/90/-45/0/45/0/-45/ 90/45/0]s，对称铺层共26层，单层名义厚度0.14 mm，总厚度3.64 mm。试验测试紧固件采用TC4抗剪切型钛合金凸头螺栓，螺栓杆部名义直径为8 mm，螺栓基本材料属性见表1。

单钉单剪螺栓连接试验件尺寸见图1(a)；局部(胶层)尺寸见图1(b)；三钉单剪螺栓连接试验件尺寸见图1(c)。其中，图1(c)指示了本文试验使用的螺栓编号，后文分别用1#、2#、3#表示Bolt 1、Bolt 2、Bolt 3。孔名义直径为8 mm，板宽度W、边缘间距e、螺栓孔间距p与螺栓直径D的比值分别为W/D=6、e/D=3、p/D=4.5，直径与厚度之比为D/t=2.20。试验件参考文献[2，12]进行设计。其中加强片的作用是保护层合板不被夹持端损伤和保障单向拉伸的对中；胶层的作用为保证粘贴应变片后上下板仍然为面接触。

表1 材料属性Table 1 Material properties

1.2 修正次弯曲的影响

在单剪连接结构中，孔边接触力沿厚度方向非均匀，必然导致次弯曲。此对钉载分配测量结果的影响不可避免。采用表面应变测量法必须对次弯曲进行限制或通过改进测量方法进行结果修正。对于碳纤维增强复合材料，由复合材料力学相关知识可知：层合板的应变可以等效为拉伸导致的中面应变和弯曲应变两部分组成，沿着厚度方向线性分布，关系表达式为

(1)

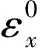
在本研究中，将由偏心载荷引起的层合板不均匀内力等效为一个均匀内力和一个附加的弯矩组合。这种分析方法在复材连接中，也类似地被Langella等[22]在分析单搭胶接中使用，对复材层合板单搭接偏心载荷的分析，有着非常好的效果。等效受力情况如图2所示。图中：Nx表示水平内力，M表示等效弯矩。

基于此，在层合板上下表面对称粘贴应变片，测量上下两面在同一水平位置的应变，由于弯矩导致的表层应变绝对值为

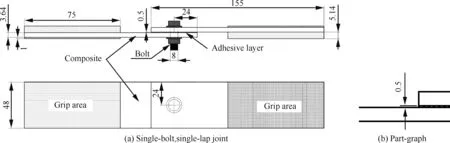
图1 连接接头尺寸参数(单位: mm)Fig.1 Dimension parameters of joints (Unit: mm)

图2 层合板受力等效图Fig.2 Equivalent stress diagram of laminated plates

(2)

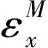
通过消除弯矩导致的应变，修正后得到由拉伸载荷导致的应变。设计的应变片粘贴布局，试验件应变片的粘贴位置如图3所示(上板)。

(3)

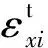
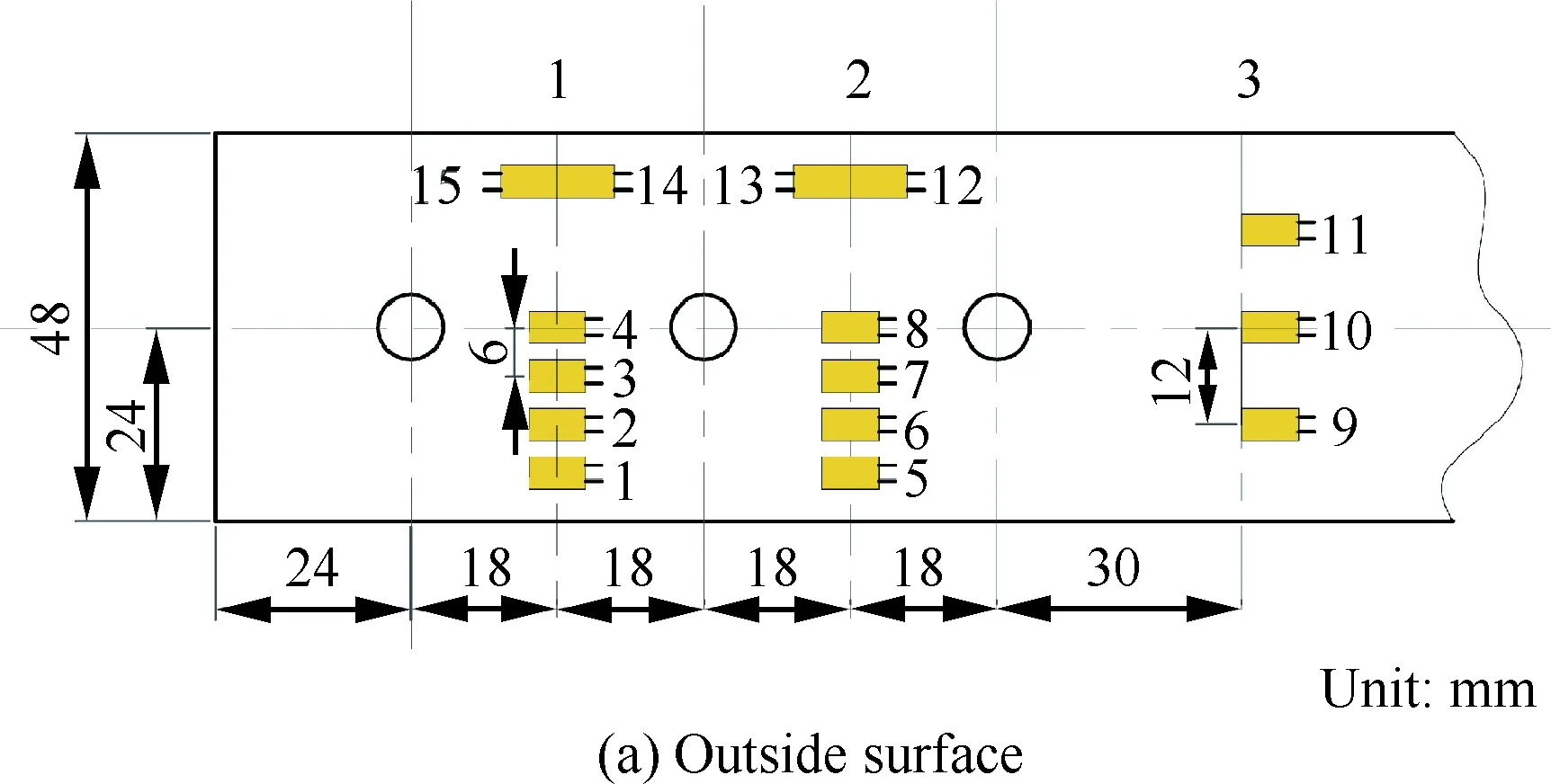
图3 应变片粘贴位置图Fig.3 Strain gauge positioning for load distribution measurement

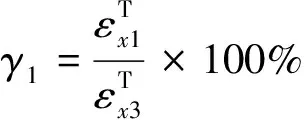
(4)

(5)

(6)

式中：γi(i=1, 2, 3)分别表示图3的区域1、2、3旁路载荷分配比例，间接表示1#、2#、3#螺栓的钉载分配比例。

但是采用这种方法测量，会产生一个新的问题：由于应变片有一定厚度且焊接处存在锡块(测量显示：应变片最大厚度在锡焊接处且不超过0.4 mm)， 使上下层合板将无法完全接触而产生大面积的空隙。为解决这个问题，试验先将应变片粘贴于层合板表面，再均匀地涂抹一层0.5 mm的胶层完全覆盖应变片(实验中：在层合板两端垫0.5 mm垫片，上胶后覆盖塑料薄膜并上压平整光滑的金属板)，然后固化。其中：固化温度为常温，时间48 h。应变片被埋在胶层中，使上下板仍然为面接触，如图4所示。

图4 固化在上板下表面的应变计Fig.4 Strain gauges solidify on lower surface of upper plate

试验通过简单、有效且经济实惠的应变计测旁路载荷法，间接测量复合材料层合板多钉单剪螺栓连接在不同条件下的钉载分配。

1.3 修正摩擦力对钉载的影响

复材螺栓连接中，施加拧紧力矩产生的摩擦力，通过面内剪切进行载荷传递。如此，表面应变间接测量的钉载分配结果并不能直接代表螺栓的承载比例，即：结果不准确。对图1(c)上板1#螺栓钉-孔位置进行水平方向受力分析，见图5，具体分析式为

图5 上板1#钉-孔处受力分析Fig.5 Force analysis of nail-hole on upper plate 1#

P1-2=Pbolt1+flam2-1+fbolt-1

(7)

式中：P1-2代表1#螺栓和2#螺栓之间层合板水平拉伸载荷；Pbolt1代表1#螺栓施加给上板1#螺栓孔的挤压载荷；flam2-1和fbolt-1分别代表下板和螺栓垫片施加给上板的摩擦力。

试验直接测量的应变是Pbolt1、flam2-1、fbolt-1共同作用导致的结果。虽然摩擦力对钉载分配的作用机理较为复杂，但通过试验测量单钉单剪连接在不同拧紧力矩下的极限摩擦力，修正钉载分配测量的结果可以对拧紧力矩对钉载分配的影响规律做出较好的揭示，且比未修正结果更准确。施加拧紧力矩的各钉承载比例，可用式(8)修正:

(8)

式中:γRi代表修正后的第i颗螺栓的钉载比例；P代表外载；fmaxi代表各钉在拧紧力矩下的极限摩擦力。

1.4 试验过程

试验采用SANSCMT5205/5305微机控制万能力学拉伸机进行单钉单剪螺栓连接单向拉伸试验，试验机最大拉伸载荷为10 t(100 kN)，加载速率为1 mm/min。拧紧力矩通过高精度扭力扳手施加。试验测量不同拧紧力矩下的极限摩擦力和载荷-位移曲线，其中每组试验件5个。

钉载分配的测量试验在天辰WES-100B万能力学拉伸试验机上完成，该拉伸试验机的最大拉力为100 kN。同组试验件数量为5件。拉伸过程中的拉力由试验机内置的拉力传感器测定。采用KD7016静态应变测量仪测量BFH120-3AA应变片在各定载下的应变值，间接测量三钉单剪螺栓连接钉载分配比例。由于本研究考虑了钉-孔间隙，故试验正式开始前仅采用100 N左右的外载进行3～5次预拉伸，消除夹持等造成的影响。复材层合板力学性能受温度影响，进行试验的实验室温度控制在(22±4)℃[23-24]。

三钉单剪连接试验件各组的名义钉-孔间隙c，见表2，共12组；对各螺栓施加不同的拧紧力矩T，见表3，共12组，见表2和表3。在试验中，施加不致层合板损伤的中小载荷，对同一个试验件通过“加载-测量-卸载拆卸-静置回复-更换拧紧力矩组合-加载”的方式，可以得到多组试验测量数据，其中：同参数的试验件每组5个，且测量结果中剔除残差值异常大的数据。其中：15 kN外载荷，对表 2-case1的试验件，施加表 3-case 2的拧紧力矩组合，各区域测量应变平均值见表4。试验测量极限摩擦力见表5。

表3 拧紧力矩配置Table 3 Configuration of bolt torque

表4 应变平均值(外载：15 kN)Table 4 Strain averages (External load: 15 kN)

表5 试验测量极限摩擦力Table 5 Measured value of critical friction

注：由于试验条件有限，5 N·m以下数据误差可能较大。

对复材单钉单剪连接，图1(a)(所有试验件均在上板下表面固化0.5 mm胶层)，进行单向拉伸试验，得到不同参数的载荷-位移曲线，见图6，c表示钉-孔间隙；T表示螺栓拧紧力矩；Dw表示垫圈外直径；fmax表示极限摩擦力。结果显示：极限摩擦力fmax受夹紧面积的影响；其他参数相同前提下，增加胶层使得峰值载荷和极限摩擦力分别下降约1.98%和4.1%，但整体吻合度高。为降低误差影响，在本文研究中，采用固定的夹紧面积来排除其对极限摩擦力测量结果的影响。得到：Dw=16 mm;P=15 kN的各拧紧力矩下的极限摩擦力见表5。

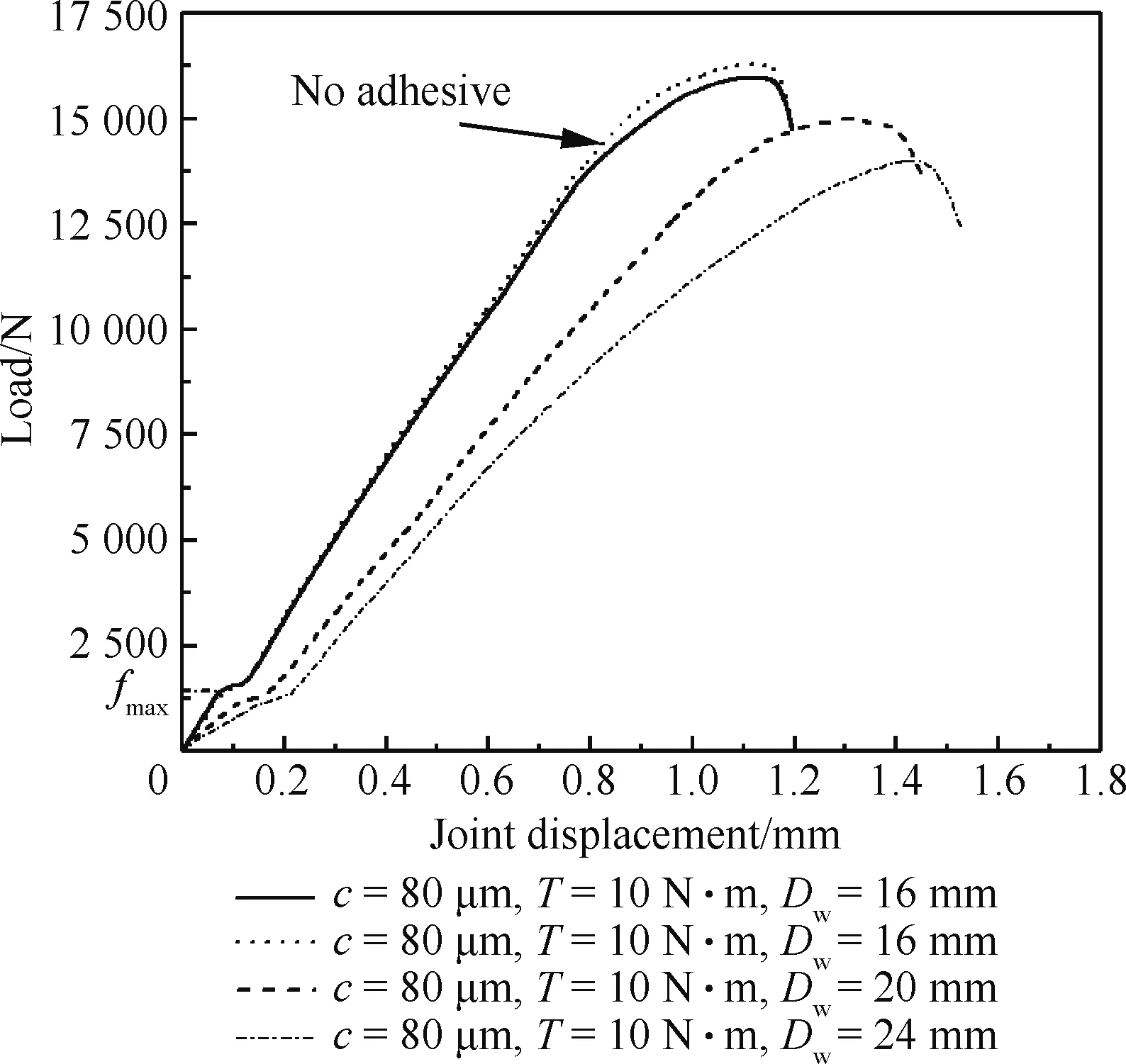
图6 试验得到的载荷位移曲线Fig.6 Experimental load-displacement curves

2 钉载分配优化模型

碳纤维树脂基复合材料层合板，一直到破坏都呈现近似的线弹性行为，几乎不具有载荷重新分配的能力[1]，但各钉承载比例随外载荷的变化会有一定变化[12,17]，所以进行钉载分配均匀化的研究，首先应当设定一个固定的外载荷。综上，本文采用低于试验测量初始参数复材三钉单剪连接极限失效载荷的50%为外载荷。在此前提下，根据试验测量各参数条件下的钉载分配比例，并构建函数模型

(9)

式中：R代表与自变量无关的待估常数量；γi代表各钉的承载比例；ci代表各钉-孔间隙；Ti代表各钉的拧紧力矩；αi、βi为待估参数；ξ为高阶无穷小量，代表误差。利用试验测量多组钉载分配数据，通过SPSS软件求解得到各待估参数值，从而得到具体某钉载比例和各参数之间的多元线性关系式。

由此，设定目标函数为

Min:f(c,T)=γmax-γmin

(10)

式中：γmax、γmin分别表示优化前(初始参数时)承担最大和最小载荷的螺栓钉载比例。函数f(c,T)是各钉承载比例的最大波动范围，描述了各钉载的不均匀程度，函数值越小，表示钉载比例越趋近于均匀化。

由于本文基于飞机装配的要求：钉-孔间隙不能超过孔径的1%；安全性需要，拧紧力矩应当小于某一最大值，即满足：

(11)

(12)

此问题为一次线性规划问题，不难证明局部最优解也是全局最优解。

3 钉载分配优化算法

将式(9)代入式(10)中可以得到

Min:f(c,T)-(R-+x-)=

(13)

设Min:g(c,T,X)=f(c,T)-(R-+ξ-)为新的目标函数，则整个问题可变为标准型线性规划。对于该类问题，可以求解的方法很多，本文采用改进的单纯形算法这一简单高效的方法进行迭代求解。该方法的基本原理是：通过引入人工变量将约束不等式转变为等式方程，依次判断可行域的顶点是否为最优解。若不是，沿着边界寻找邻近点继续判断是否为最优解。依次迭代，直至找出最优解。算法的基本过程如下：

2) 选取一个初始基本可行解，并根据有关信息制作单纯形表。

若否，则进入下一步。

4) 判断目标函数在可行域内是否有下界，无下界，则根据最小比值定则制定指标，进行转轴运算，得到新的基本可行解，转步骤2)。

4 均匀化算例及验证

4.1 试验测量准确性分析

试验测量复材层合板三钉单剪螺栓连接(图1(c))，钉载分配比例结果见图7，其中各钉均施加2 N·m的拧紧力矩。

从图7可以看出：复材三钉单剪连接结构的钉载分配非常不均匀。其中，未修正次弯曲影响的结果误差太大。通过应变修正次弯曲影响后的结果：图7(a)中，1#螺栓和3#螺栓钉载比例明显高于2#螺栓；图7(b)中，1#螺栓和3#螺栓的钉载比例远高于2#螺栓，且由于拧紧力矩和2#钉-孔存在的间隙，导致5 kN外载荷时，2#螺栓的钉载比例异常的小。修正后的三钉单剪连接钉载分配结果与文献[2]理论计算结果以及文献[12]测量得到的钉载分配规律相吻合，准确性较修正前大大提高。

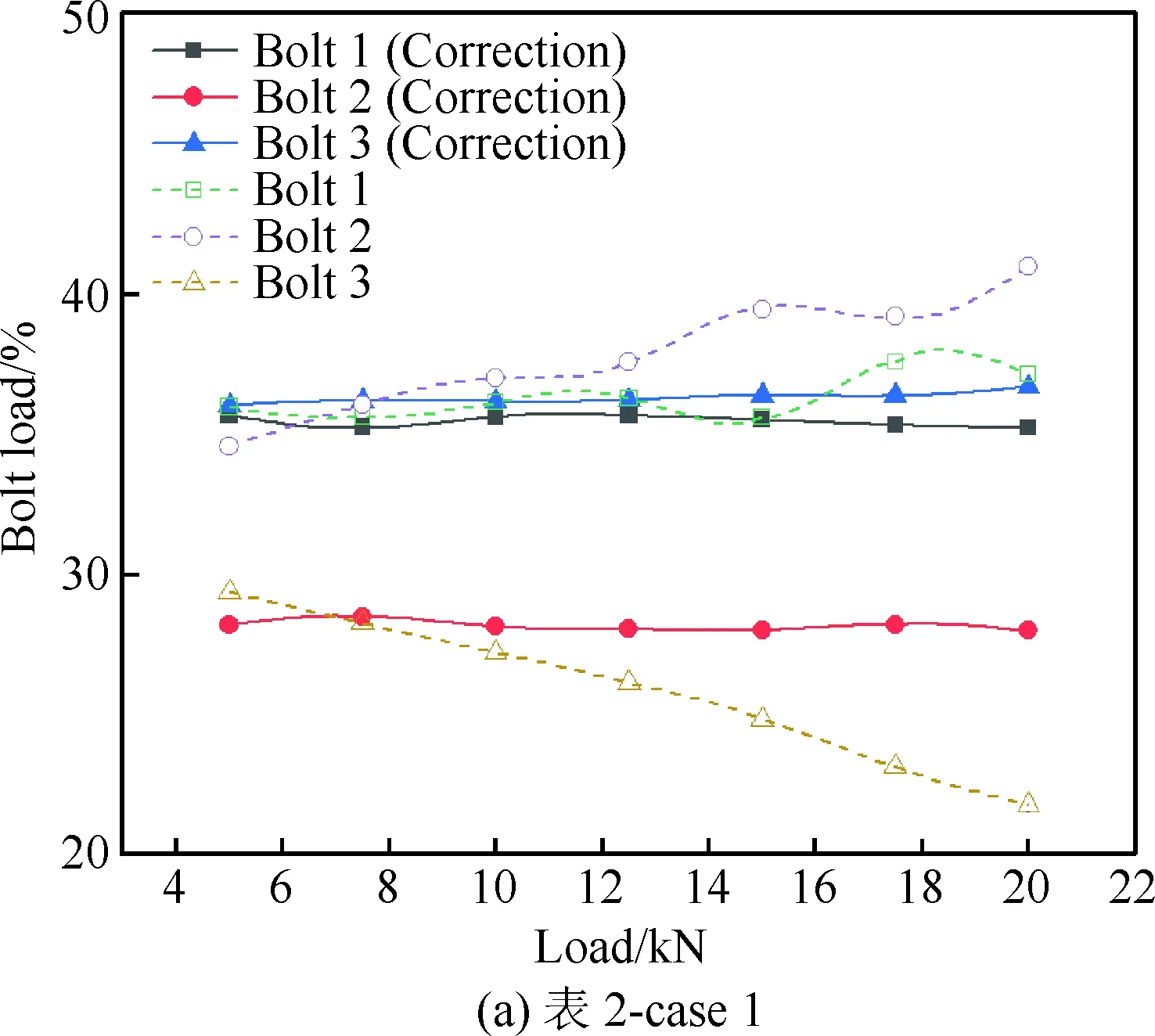
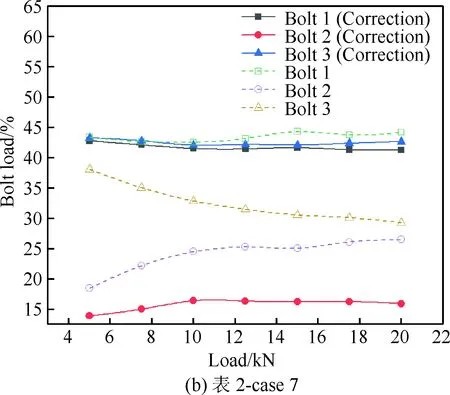
图7 钉载分配测量结果Fig.7 Results of measurement on pin-load distribution

对各钉-孔名义间隙均为0 μm的试验件分别施加表 3-case 1-5的拧紧力矩组合，并测量钉载分配，其结果见图8。其中未使用极限摩擦力修正的结果见图8(a)，使用极限摩擦力修正的结果见图8(b)。

图8(a)的结果显示：未使用极限摩擦力修正，随着首、尾螺栓拧紧力矩的增加，首、尾螺栓的钉载比例略有增加但无明显变化。这是由于：此时应变测量间接得到的仅仅是旁路载荷分配结果；拧紧力矩强化钉-孔周围层合板刚度。通过极限摩擦力修正后，图8(b)，结果显示：当增大首、尾钉的拧紧力矩，复材三钉单剪连接钉载分配趋于均匀化，此结果和文献[4]的研究相吻合。故通过极限摩擦力的修正，可以减少系统误差，测量钉载分配比例相比于未修正的结果更加准确。

本文采用修正后的试验测量结果进行钉载分配优化计算。

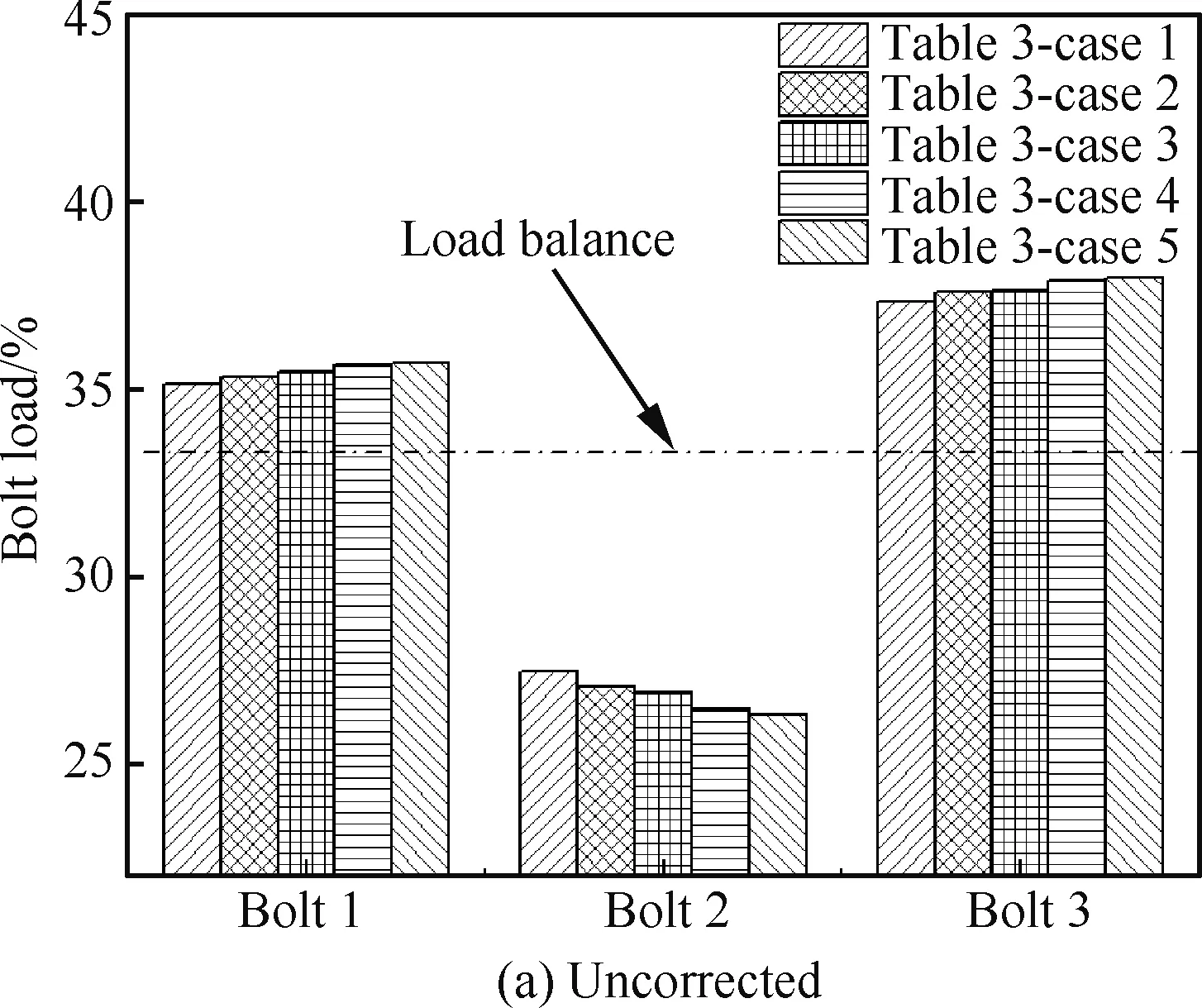
图8 拧紧力矩对钉载分配的影响Fig.8 Effect of variable bolt torque on pin-load distribution

4.2 三钉单剪连接均匀化求解结果

选用15 kN外载荷的试验数据进行载荷均匀化求解。最大钉-孔间隙：0.01D，选定最大拧紧力矩：10 N·m[1]，其中手动拧紧力矩(Finger)约为0.5 N·m[11-12]。复合材料三钉单剪连接优化结果见表6。

从表6可以看到：优化前，承担载荷最大的3# 螺栓钉载比例为36.06%，较承载最小的2#螺栓钉载比例28.24%高约27.69%。优化后，仅在承载较大钉-孔位置，引入符合飞机装配要求的钉-孔间隙，不能直接达到钉载分配均匀化；通过在承担载荷较大的钉-孔位置引入间隙配合以及较高的拧紧力矩，其钉载比例有了明显的降低，3# 螺栓的钉载比例仅33.45%，较优化前降低约7.9%，承载比例最小的2#螺栓钉载比例上升为33.17%，较优化前上升约17.46%，各螺栓几乎均匀承载。

由于试验件的加工无法保证参数的连续，故在试验验证中，各钉采用与优化结果接近的钉-孔间隙和拧紧力矩进行验证。并通过改进的应变法测量15 kN外载荷下各钉承载比例，具体参数设置见表7。

优化后，复材三钉单剪连接钉载分配试验测量和计算结果对比见图9，结果显示：试验测量结果与优化计算结果十分接近。图9(a)仅引入符合飞机装配要求钉-孔间隙，各钉承载比例结果最大相差2.3%；图9(b)通过在承担载荷较大螺栓位置引入钉-孔间隙和拧紧力矩1#、2#、3#螺栓钉的钉载比例结果相差分别为：0.05%、1.42%、1.34%， 最大相差为1.42%，试验测量的各螺栓的钉载比例几乎均匀相等，验证计算结果较为准确。

表6 钉载均匀化结果Table 6 Pin-load homogenization results

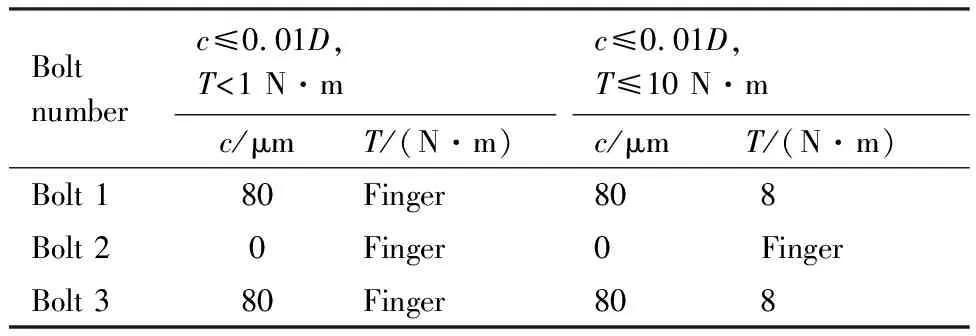
表7 三钉单剪螺栓连接钉载均匀化参数配置Table 7 Parameters of joint configuration for three-bolt,single-lap joints pin-load homogenization

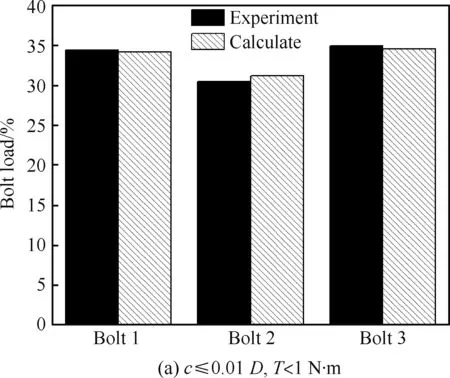
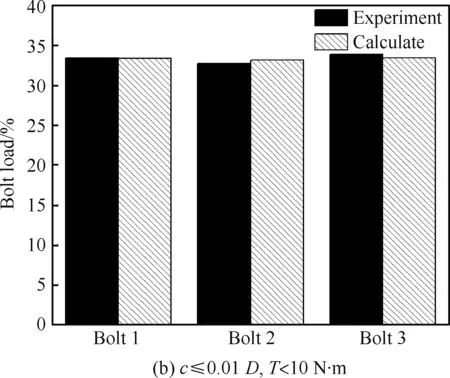
图9 优化结果(外载：15 kN)Fig.9 Optimization results(External load:15 kN)

4.3 强度对比

载荷均匀化的最终目的是提高连接的承载能力，通过失效性试验验证计算得到的均匀化效果是必要的。对优化前后三钉单剪连接件进行单向拉伸试验，得到失效载荷见表8。结果显示：钉载均匀化可提高复材三钉单剪连接的承载能力，平均提高约10.8%。

载荷均匀化会改善多钉连接结构的失效形式。对于载荷非均匀化的复材多钉连接，首尾钉孔处的旁路载荷几乎为100%外载荷。由于存在挤压载荷和旁路载荷的耦合以及应力集中，故首尾钉承载比例越高，越容易导致首尾钉孔处发生拉伸失效。优化前，首尾钉孔处拉伸失效见图10。

经过钉载分配均匀化后，试验件承载更高，且多组优化参数的试验件，失效形式均为相对较安全的钉孔挤压失效：1#、2#、3#螺栓钉-孔均发生挤压失效，见图11。同时也可以看到：由于螺栓承载沿厚度方向非均匀，以及垫片挤压外侧孔等原因，内外侧失效程度不同，内侧孔挤压变形量更大，钉载分配均匀化后层合板改善钉-孔周围应力分布以提高连接结构强度还需后续进行更进一步研究。试验结果验证了该参数配置下的钉载比例均匀化结果较好，且有效地改善了三钉单剪连接的力学性能，提高了连接结构的安全性。

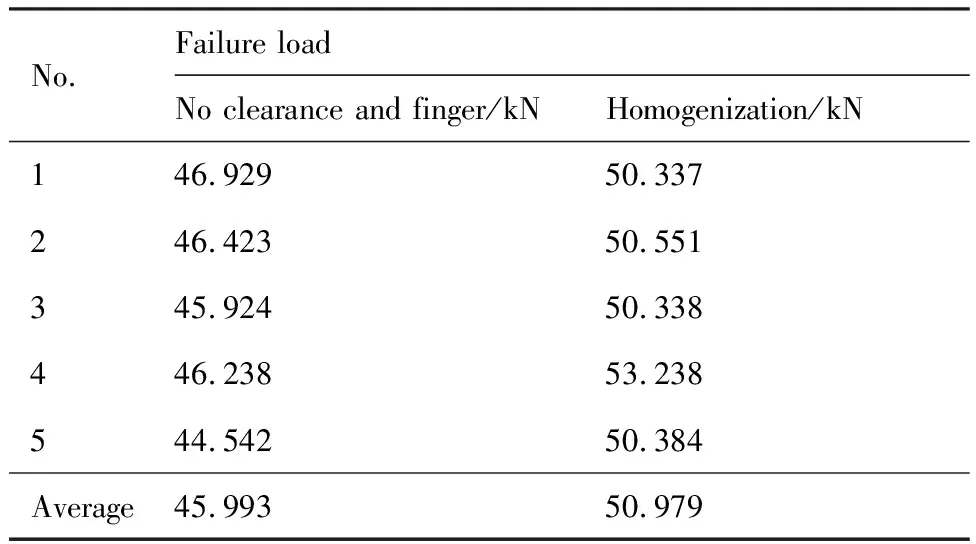
表8 三钉单剪连接失效载荷Table 8 Failure load of three-bolt, single-lap joints

图10 拉伸失效(失效载荷：46.929 kN)Fig.10 Tensile failure(Failure load: 46.929 kN)

图11 挤压失效(失效载荷：50.551 kN)Fig.11 Bearing failure (Failure load: 50.551 kN)

5 结 论

1) 给出了考虑间隙和拧紧力矩的复合材料多钉连接钉载分配均匀化的线性规划优化模型，并给出了求解方法。

2) 根据本文的优化算法，对复材层合板三钉单剪连接结构，实现了钉载分配均匀化的设计目标。

3) 算例结果显示，对各钉采取不同的间隙配合和拧紧力矩的方法能够有效地改善复合材料多钉连接钉载分配的均匀性。优化后三钉单剪连接结构最高承载比例下降约7.9%，最小钉载比例上升约17.46%，各钉孔几乎均匀承载。

4) 对算例的优化结果采用试验测量进行了验证，并通过最终失效验证。结果表明：以优化结果作为钉-孔间隙和拧紧力矩设计值，钉载分配近似均匀分配；连接承载能力提高了约10.8%，且明显改善失效形式为钉孔挤压失效。载荷均匀化提高了复合材料多钉连接的综合力学性能。

该方法计算简单、效率较高，对复合材料多钉连接的钉载分配设计具有重要的工程应用价值。