不同后掠角大展弦比复合材料机翼气动特性

刘文一，杨培源，李厚旭

（91550部队，辽宁 大连 116023）

0 引言

高空长航时飞行器由于具有飞行高度高、在空时间长等特点，其机翼往往采用非常大的展弦比，且因其结构质量要求足够低，这便使得机翼在气动载荷作用下弹性变形很大[1]。机翼多采用板壳单元，因此其刚度不大，但在飞行过程中受到气动力影响后会产生弹性变形。这个弹性变形会使机翼产生新的附加气动力，而此附加的气动力又会使机翼产生新的附加变形，新的附加变形又使机翼产生新的气动力，如此不断重复耦合，使得机翼最终出现颤振现象[2]。

从空气动力学角度看，以机翼是否处于失速攻角的状态出发，颤振可分为两类：一类是机翼处于失速攻角状态下发生的颤振，称为失速颤振；另一类是机翼不处于失速攻角状态下发生颤振，称为经典颤振[3]。

为了使机翼在飞行的过程中避免出现颤振，须给出机翼的临界颤振速度和发生颤振时翼尖处最大垂直位移，从而进一步给出飞行器的安全速度区间，使飞行器飞行速度处在安全区间内，这样可避免颤振的发生[4]。因此，有必要研究大展弦比复合材料机翼的气动特性，将其作为高性能机翼研制的理论参考。

1 载荷模型

1.1 气动力模型

机翼进行气动特性研究时，若将其作为线性结构进行分析，则其基础是机翼的小变形假设，而大展弦比机翼弹性变形往往较大，因此经典的小变形线性梁理论不再适用，而应该用非线性梁理论[5]。非线性梁考虑了大变形引起的应变与位移的非线性关系，相比于经典的线性梁模型，其更能真实地反映机翼的变形与运动的情况，因此，可用它来研究机翼的气动特性与响应特征[6]。

机翼在飞行器飞行过程中发生振动时，机翼受到非定常气动力[7]。如果仅考虑机翼扭角引起的定常气动力，则可只研究单个振动周期内二自由度机翼的气动力的能量平衡，从能量输入的角度来研究机翼颤振问题[8]。

当机翼在弯曲自由度上以浮沉自由度向上振动π/4 相位时，气动力在整个振动周期中做正功，机翼就会在气动力的激励下发生颤振，即经典弯扭颤振[9]。

如果沿着某根弦将机翼剖开，则可得到单位展长的二元机翼模型。其有2 个自由度，分别是刚心的浮沉运动自由度和绕刚心的转动自由度[10]，如图1所示。

图1 二元气动力平板模型Fig.1 Plate model of binary aerodynamic

图1 中：b 为半弦长；E 为刚心；aˉ为刚心到弦几何中点之间的距离占半弦长b 的百分比；h 为浮沉位移；α为俯仰角；V 为来流速度。

二元机翼在空气中运动时，其浮沉运动与俯仰运动均为简谐运动，频率为ω，单位展长机翼所受的气动升力L 与作用在刚心上的俯仰力矩Tα可由Theodorsen气动表达式给出[11]：

式（1）（2）中：ρa为空气密度；k=为无量纲折合频率。

C( k )为Theodorsen函数：

Jn和Yn分别为一类和二类Bessel 函数。则C( k)的实部、虚部为：

k 为折合频率，如果其值非常小，则可以引入准定常流假设[13]。

即当k →0 时，C( k )→1。则Theodorsen 气动升力、力矩又可表达为：

1.2 气动载荷模型

有了气动力的表达式，则可根据飞行器结构辨识出其所受的气动载荷[14]。飞行器在飞行过程中，其所受的气动载荷主要与飞行速度、飞行姿态、飞行高度和飞行器气动参数等有关。在研究时，为了方便仿真计算，可将气动参数用样条曲线的形式表达，气动参数主要有升力系数、阻力系数、滚转力矩系数、滚转阻尼力矩系数和压心系数。

气动力：

式（10）中：cx、cy和cz为气动系数；q 为气动力；S 为迎流面积。

阻尼力矩：

静稳定力矩：

式（12）中：xm为动压系数；xp为静压系数。

R 可在速度坐标系里得到；阻尼力矩Md和静稳定力矩MR可在飞行器体坐标系下得到。

将从速度坐标系内得到的气动力R 转化到飞行器体坐标系：

2 计算模型

2.1 模态分析模型

1个N 自由度的线性系统的运动微分方程可以表示为：

式（14）中：M 为系统的质量矩阵；K 为系统的刚度矩阵；C 为系统的阻尼矩阵；x¨ 为节点的加速度；x˙为节点的速度；x 为节点的位移；F 为节点激振力。

由于振型矩阵与质量、刚度矩阵具有正交关系，因此其相对的阻尼矩阵也可以近似对角化：

这样，相互耦合的具有N 个自由度的系统方程组经过正交变换，得到在模态坐标下相互独立的具有N个自由度的系统方程组，经过解耦，第i 个方程为：

从式（16）可知：模态坐标系下，1个N 个自由度的系统响应等于在N 个模态坐标下单自由度系统的响应之和；采用归一化方法使模态质量归一，且记归一化模态振型为Φ。即：

105 体外膜肺氧合救治危重患者的临床分析：附 18例报告 杨 帆，王 军，丁金奎，樊美珍，陈佳一，吴 俊，陈晓芳

ωi=为系统的模态固有频率，表示1 个具有N 个自由度系统有N 个固有频率。

2.2 颤振速度计算模型

目前，颤振速度的计算大多采用K 方法，其基本思路是在分析的过程中先假定系统为无阻尼结构，然后引入人工结构阻尼D，则结构的振动方程变为[15]：

其中，2个自由度上的衰减结构阻尼力为：

式（19）中：gh和gα为引入的人工阻尼系数。将这2个系数带入振动方程可得：

根据方程特点，可将其转化为广义特征值问题：

3 仿真模型

3.1 几何模型

某大展弦比飞行器为了获得最佳的飞行性能，共设计了后掠角分别为0°、5°、10°、15°、20°、25°和30°共7种复合材料机翼式[17]，其结构参数见表1。

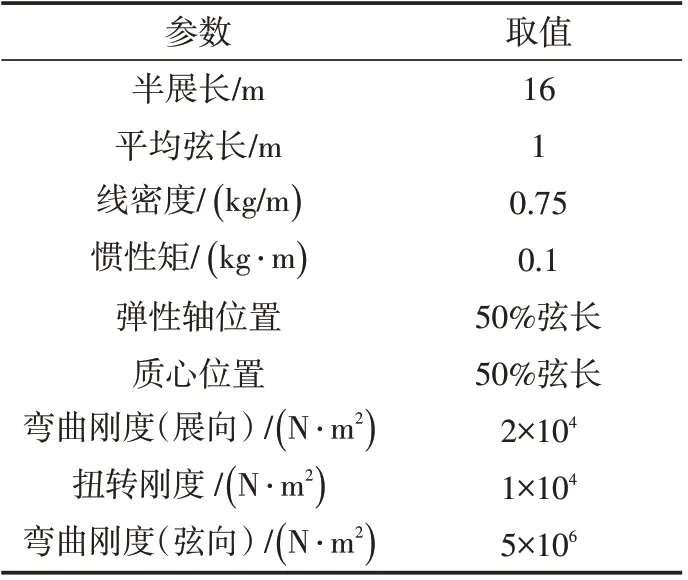
表1 机翼结构参数Tab.1 Parameters of wing

图2 0°后掠角机翼Fig.2 Wing of 0°sweepback angle

图3 5°后掠角机翼Fig.3 Wing of 5°sweepback angle

图4 10°后掠角机翼Fig.4 Wing of 10°sweepback angle

图5 15°后掠角机翼Fig5 Wing of 15°sweepback angle

图6 20°后掠角机翼Fig.6 Wing of 20°sweepback angle

图7 25°后掠角机翼Fig.7 Wing of 25°sweepback angle

图8 30°后掠角机翼Fig.8 Wing of 30°sweepback angle

3.2 材料模型

机翼由复合材料制成，采用C/C材料（其力学性能如表2所示）针刺结构，预制体是由多层正交碳纤维布以厚度方向穿刺制成[18]。该机翼中的碳纤维在平面内以0°、45°和90°方向排列，仅有少量沿厚度方向排列。碳纤维的力学性能参数在0°、45°和90°方向上相同，而在厚度方向上的力学性能参数约为0°、45°和90°方向参数的1/8。

表2 C/C复合材料的力学性能Tab.2 Mechanical performance of C/C composite material

3.3 速度模型

飞行器以一定速度飞行，单位m/s，计算时将其分解为参考坐标系上的速度矢量[19]：

4 计算结果

4.1 模态分析

大展弦比飞行器主要用于长航时高空平飞作业，故分析了飞行器在飞行高度20 km 平飞时的模态，飞行马赫数为0.7，空气密度为0.088 9 kg/m3。得到了后掠角分别为0°、5°、10°、15°、20°、25°和30°共7 种机翼的前十阶模态，得到了模态频率，如图9所示：

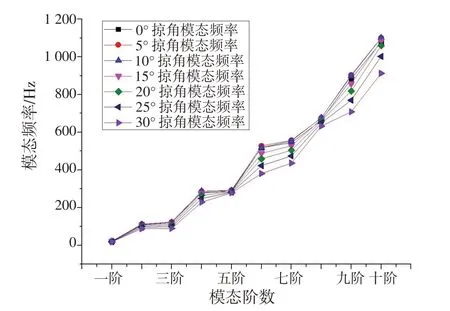
图9 不同后掠角机翼前十阶模态频率Fig.9 First tenth order modal frequencies of different sweepback wings

由图9可以看出，7种不同后掠角的机翼随着后掠角增加，其对应的各阶模态频率逐渐减小。7 种不同后掠角的机翼第一阶和第五阶模态频率相同。同时得到了7种不同后掠角的机翼在模态频率相同时的模态振型，如图10～16 所示（图中上方为第一阶模态振型，下方为第五阶模态振型）。

图10 0°后掠角机翼第一阶和第五阶模态振型Fig.10 1st and 5th order modal shapes of 0°sweepback wing

图11 5°后掠角机翼第一阶和第五阶模态振型Fig.11 1st and 5th order modal shapes of 5°sweepback wing

图14 20°后掠角机翼第一阶和第五阶模态振型Fig.14 1st and 5th order modal shapes of 20°sweepback wing

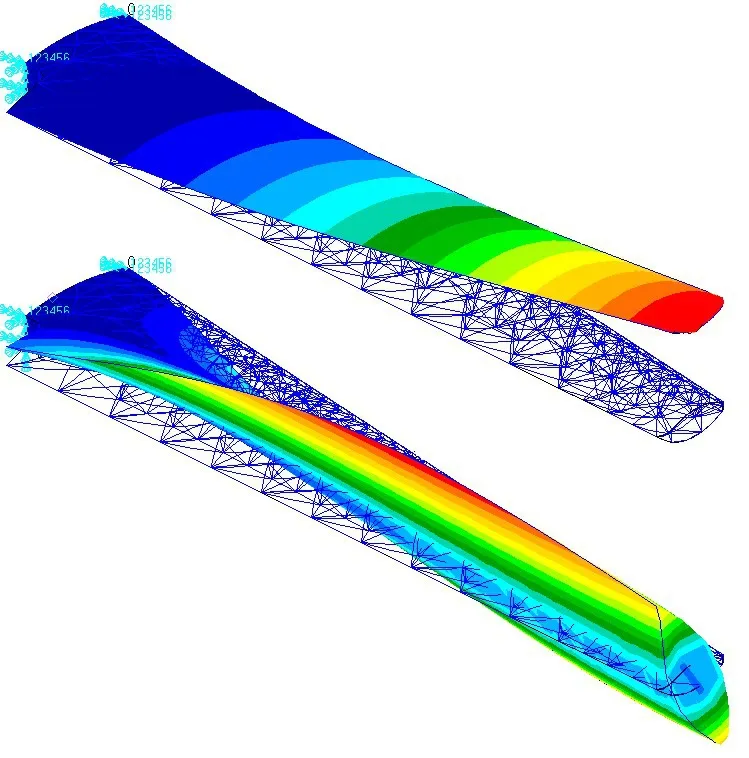
图15 25°后掠角机翼第一阶和第五阶模态振型Fig.15 1st and 5th order modal shapes of 25°sweepback wing

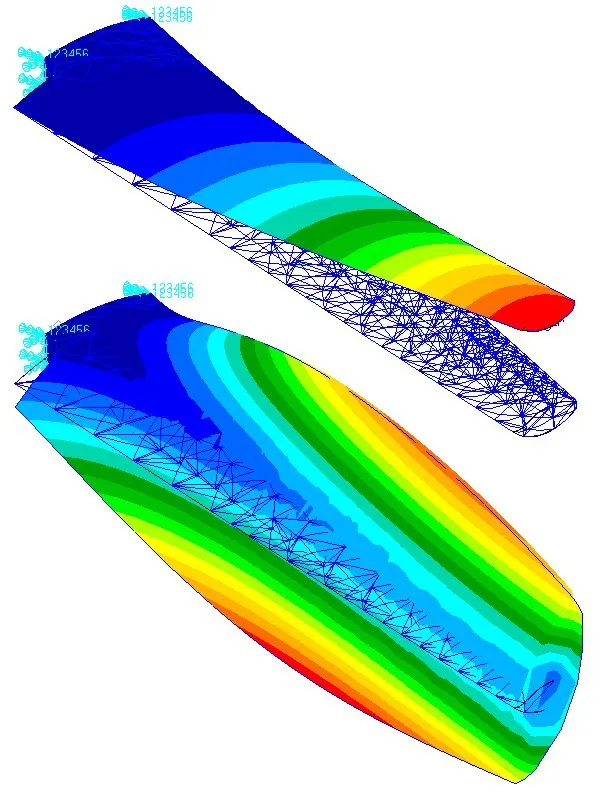
图16 30°后掠角机翼第一阶和第五阶模态振型Fig.16 1st and 5th order modal shapes of 30°sweepback wing

由图10～16 可以看出，不同后掠角机翼的第一阶模态振型具有相似性，均为垂直弯曲振型。对于模态频率相同的第五阶模态振型，0°、5°和10°机翼模态振型相同，均为二阶弯曲振型；15°、20°、25°和30°机翼模态振型相同，均为一阶弯扭耦合振型。

4.2 颤振速度计算

在4.1节的模态分析结果基础上，计算7种不同掠角机翼的颤振速度[7]，如图17所示。

图17 不同后掠角机翼颤振速度曲线Fig.17 Flutter velocities curve of different sweepback wings

从图17 看出，随着后掠角的增大，颤振速度不断升高，这是因为随着后掠角的不断增大，机翼的弯扭耦合减弱，使得机翼弯曲变形和扭转变形不断减小，这与模态分析的结果相一致。具体数值如表3所示。

表3 不同后掠角机翼颤振速度Tab.3 Flutter velocities of different sweepback wings

30°后掠角时，颤振速度为244.6 m/s，超过了飞行器巡航飞行速度180 m/s；15°后掠角时，颤振速度为170.1m/s，低于飞行器巡航飞行速度180 m/s。

得到7 种后掠角机翼颤振速度后，再对机翼进行动力学响应分析，则可得到飞行器飞行速度达到机翼颤振速度时翼尖处最大垂直位移，如图18所示。

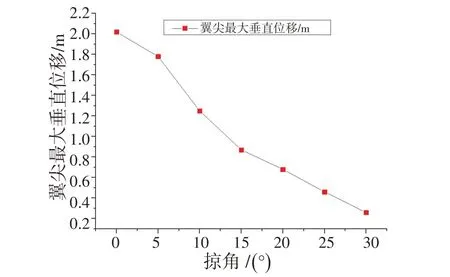
图18 不同后掠角机翼在颤振速度时翼尖最大垂直位移曲线Fig.18 Maximum vertical displacement curve of wing trip at flutter velocity for different sweepback wings

从图18 看出，随着后掠角增大，机翼达到颤振速度时其翼尖处的最大垂直位移逐渐减小。其值如表4所示。

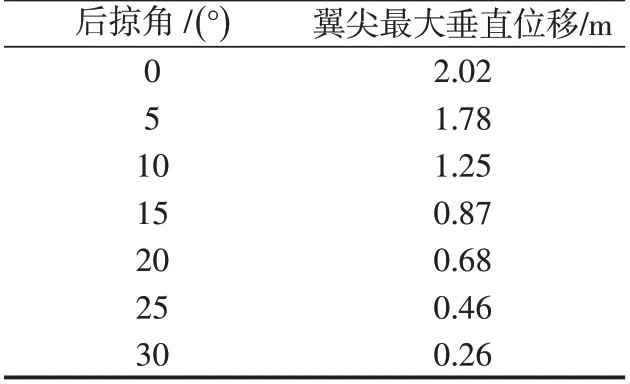
表4 不同后掠角机翼在颤振速度时翼尖最大垂直位移Tab.4 Maximum vertical displacement of wing trip at flutter velocity for different sweepback wings

0°后掠角机翼最大垂直位移最大，为2.02 m；15°后掠角机翼达到其颤振速度时最大垂直位移0.87 m，处于设计门阈值0.9 m以内。

5 结论

本文建立了0°、5°、10°、15°、25°和30°共7 种后掠角机翼载荷模型，推导了模态分析和颤振速度计算公式，分析了7种不同后掠角机翼的模态，仿真计算得到了7种不同后掠角机翼的颤振速度和发生颤振时翼尖的最大垂直位移，得出以下结论。

1）7种后掠角机翼的第一阶模态频率和第五阶模态频率相同。第一阶振型均为垂直弯曲振型。对于第五阶模态振型：0°、5°和10°机翼模态振型均为二阶弯曲振型；15°、20°、25°和30°机翼模态振型均为一阶弯扭耦合振型。

2）7 种后掠角机翼随着后掠角的增大，颤振速度不断升高，这是因为随着后掠角的不断增大，机翼的弯扭耦合减弱，使得随着机翼弯曲变形和扭转变形不断减小，这与模态分析的结果相一致。同时，机翼随着后掠角的增大，达到颤振速度时其翼尖处的最大垂直位移逐渐减小。

3）30°后掠角时，颤振速度为244.6 m/s，超过了飞行器飞行速度180 m/s；15°后掠角时，颤振速度为170.1 m/s，处于飞行器安全飞行速度180 m/s以内；0°、10°和15°后掠角机翼达到颤振速度时最大垂直位移均未超过设计值0.9 m；15°后掠角机翼达到其颤振速度时翼尖最大垂直位移0.87 m，处于设计门阈值以内。综合分析，机翼后掠角为15°时，颤振速度和翼尖最大垂直位移均在安全范围内。因此，后掠角为15°，展弦比为26的机翼为设计的最优值。