基于Stacking集成学习的飞行模拟器设备故障预判
王 伟,周晓光,卓靖升,王 刚
(1.91475部队,辽宁 葫芦岛,125001;2.92635部队,山东 青岛,266200)
0 引言
飞行模拟器具有安全、经济、高效等特点,已经成为飞行员培训体系中重要组成部分[1-2]。随着飞行模拟训练在飞行员培训中所占的比例越来越高,急需提升飞行模拟器故障快速应急处置能力,精准预判飞行模拟器设备故障并快速处理,以减少对模拟训练的影响。
飞行模拟器运行环境苛刻,使用频率高、时间长,其设备存在故障率较高、寿命较短等特点。另外,飞行部队飞行模拟器维护人员能力有限,维护经验、手段不足,这也成了制约飞行模拟器使用[3-4]的因素。因此,基于人工智能,及时准确判断飞行模拟器设备的故障状态,对于后续如何采取快速有效的控制手段,缓解飞行部队飞行模拟器设备维护压力具有重要意义。
针对飞行模拟器设备的故障预判:文献[5]结合了故障树分析法和专家系统,实现了对飞行模拟器的故障诊断,并构建了相关的专家知识库;文献[6]基于BRB 专家系统,实现了对飞行模拟器的故障诊断,并在此基础上开展后续的容错控制研究;文献[7]通过特征工程提取数据的相关特征,采用随机森林对设备故障进行预判;文献[8]建立了平台级PHM 系统的整体结构,对设备的故障诊断和寿命预测开展了研究。
然而,由于飞行模拟器系统组成复杂,设备存在故障数据量大、维度高等特点,传统的基于模型的故障诊断方法具有较大的局限性[9-12]。基于数据驱动的机器学习方法无须建立研究对象的数学模型,通过对故障状态数据进行训练,可以实现对设备的故障诊断研究。
1 数据特征工程
受运行环境的影响,从设备直接获取的故障数据存在异常值和缺失值,这类数据不利于机器学习模型的训练和使用,因而有必要对这些数据进行预处理。
1.1 缺失值与异常值处理
首先,对数据样本进行缺失值判断。对于缺失的数据,采用正态分布法进行补全。对于故障数据时间序列向量X=[x1,x2,...,xn],计算该向量的均值和方差,生成符合正态分布的时间序列,如式(1)所示:
式(1)中:μ 表示正态分布序列的均值;σ 为方差。
其次,采用箱形图法识别数据的异常值。定义如式(2)(3)所示的范围:
式(2)中:P1为数据集时间序列的第1个四分位数;P3表示数据集时间序列的第3 个四分位数。式(2)表示阈值判断范围。
通过计算故障数据样本中各时间序列的阈值范围,构建箱型图。对于不满足该阈值范围的数据,认为是异常值,可将其剔除。
1.2 故障特征提取
特征提取的目的是在降低原始数据维度的同时,获得可以加快机器学习模型训练速度的特征集合。核主成分分析法(KPCA)对于高维度、非线性的数据具有较好的处理能力。通过引入核函数,该方法可以将低维空间内的非线性数据转化为高维度空间的线性数据,再根据累计特征贡献率决定要提取的特征向量,从而避免了人为因素的影响。linear、sigmoid、poly、RBF等都是常见的核函数。
通过非线性函数Φ()· 将数据集D 映射到高维空间F 中,高维空间F 中样本的协方差矩阵CF如下:
通过式(5)求解CF的特征值:
式(5)中:λ 为CF的特征值;VL为对应的特征向量。
Kij=k(xi,xj)=φ(xi)·φ(xj) 为核函数,它可以将问题转化为求解K 中的特征向量,即寻找高维核空间的主元方向,计算方法如式(6)所示:
依据特征贡献率,取从大到小排列的前k 行为特征提取后的降维数据。
2 Stacking集成学习模型
卷积神经网络(CNN)、BP 神经网络以及随机森林(RF)是数据分类及故障预判等问题处理中最常用的方法,其优缺点各有不同。CNN在数据的特征提取以及降维减参等领域表现出较好的性能,擅长处理强关联的工业过程数据[13];BP神经网络具有较大的容错能力,但收敛速度慢且易于过拟合[14];RF 对异常值和噪声具有很高的容忍度,并且不易出现过拟合现象,但对于小数据或者低维数据,诊断准确率较低[15-16]。
2.1 Stacking“两阶段”模型
Stacking“两阶段”模型如图1 所示。“两阶段”是指:第一阶段即“基分类器”,其作用是对样本进行初步判断,并将结果汇总成新的训练集;第二阶段即“元分类器”,通过第一阶段的输入训练集获得最终的判断结果。“两阶段”的优点是能够避免单个模型精度不足的问题。
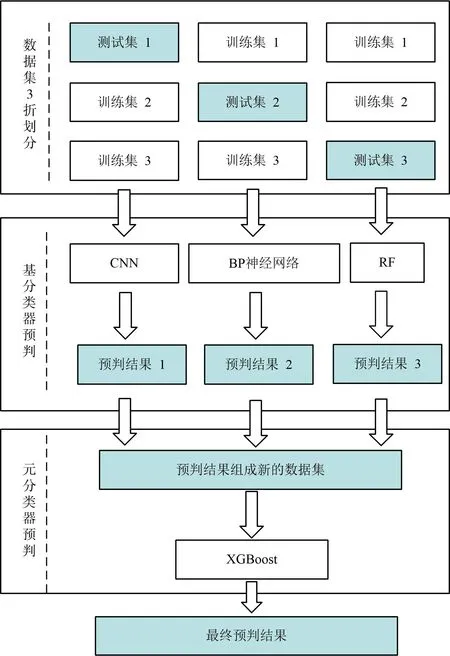
图1 Stacking“两阶段”模型示意图Fig.1 Schematic diagram of two-phase Stacking model
构建Stacking集成学习的目的在于融合各个单一分类器的优点,进而提升模型的故障预判准确率。其基本思想是:首先,使用各个基分类器对故障样本进行识别和判断,获得多个结果;将得到的多个结果作为训练样本输入到元分类器中训练和使用,获得最终的诊断结果。
2.2 交叉验证训练策略
采用交叉验证的思想是为了避免在模型的训练过程中出现过拟合的现象[17-19]。对于经过特征提取后的故障样本Y={(xi,yi),i=1,2,...,n},xi表示故障数据集的特征序列,yi表示对应的故障类型。对于本文的3个基分类器,故障样本Y 被随机划分为3个样本集,分别为Y1、Y2、Y3。基分类器1对故障样本的诊断结果为yp1=(y~1,y~2,...,y~n),以此类推,3个基分类器的分类结果则可以表示为Ynew=(yp1,yp2,yp3)T,其中,Ynew是元分类器XGBoost的训练样本。在此基础上,对样本数据进行归纳,得到最终的分类结果。模型的总体思路如图2所示。
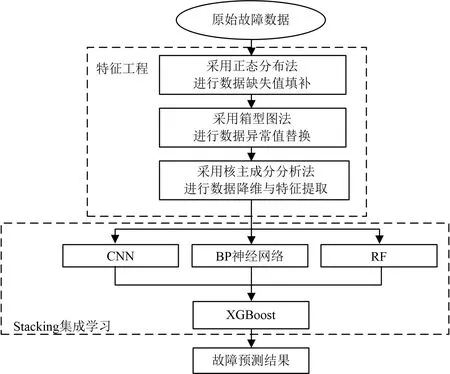
图2 模型流程图Fig.2 Model flow chart
3 算例分析
本文使用KEEL机器学习公共数据集中的7组数据,通过验证本文所构建的Stacking 集成学习模型在该数据集中的分类准确率,证明本文所提方法在设备故障预判领域的有效性。
该数据集所包含的各组数据具有不同的数据量和特征维度,较为适合用于模拟智能设备在故障时的运行数据。所选择的数据样本信息如表1所示。
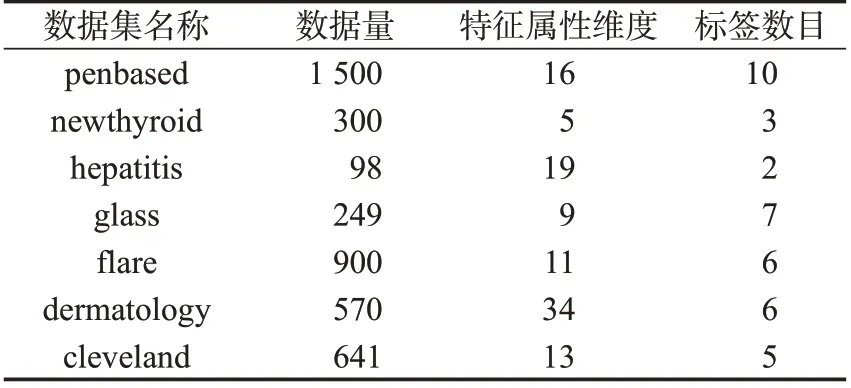
表1 数据集样本信息Tab.1 Data set sample information
表1中:数据量表示各数据集的样本数目;特征属性维度是指该数据集所包含的用于模型训练的特征的个数;标签数目表示该数据集中样本的类别数目。
将各数据集样本按照7 ∶3 划分训练集和测试集,目的是获取合适数目的训练样本和测试样本。分别使用正态分布法和箱型图法对上述数据集样本进行缺失值填补和异常值替换,同时采用KPCA对数据集样本进行特征提取与数据集降维。经过上述处理后的数据集样本数量和维度,如表2所示。
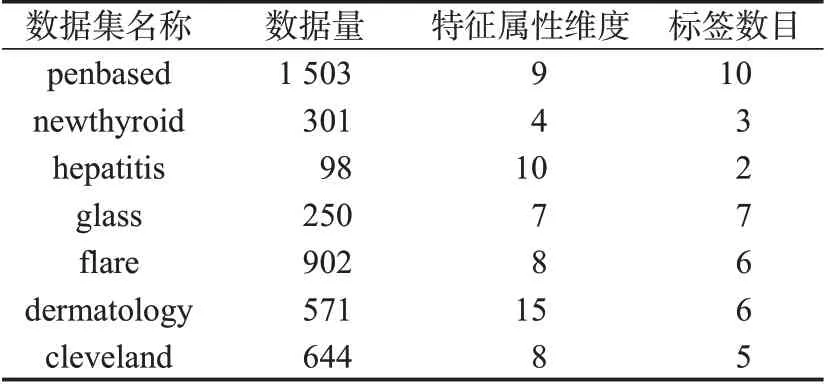
表2 经过特征工程处理后的数据集样本信息Tab.2 Sample information of data set after feature engineering processing
从表2可以看出,经过特征工程处理后,样本数据集的特征属性维度发生较大的变化,这是因为KPCA的降维效果使得原始数据集的特征属性维度得到降低,这也意味着经过特征提取后的数据具有更加精简的数据结构。
将表2 中的数据集分别输入到CNN、BP 神经网络、RF以及本文所构建的Stacking集成学习模型中进行训练和测试,分别获取4 种模型在样本数据集中的预判准确率。值得一提的是,本文所构建的Stacking集成学习模型可以直接使用CNN、BP神经网络和RF对样本数据集的预判结果,即将上述三者的预判结果进行汇总,得到最终的故障预判结果,如表3所示。
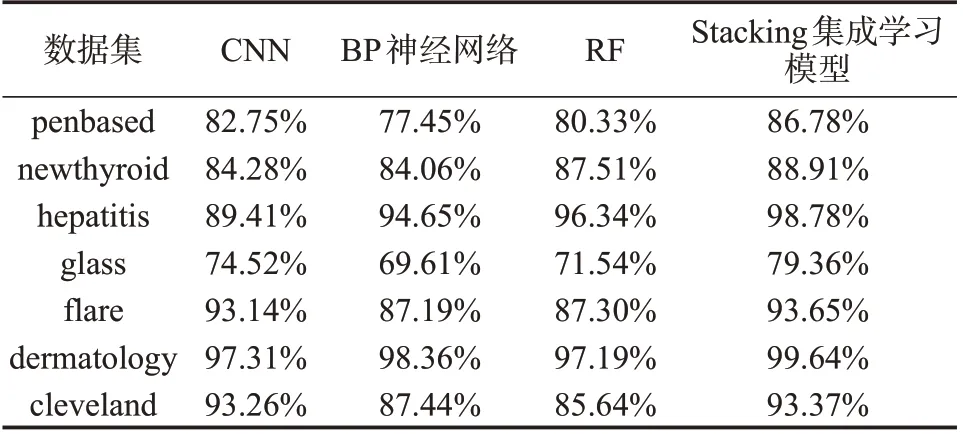
表3 3种模型与Stacking集成学习模型的预判准确率Tab.3 Prediction accuracy of three models and the Stacking integrated learning model
为了更直观比较本文所构建Stacking集成学习模型对于故障预判准确率的提升,绘制了如图3 所示的各模型预判准确率对比图。
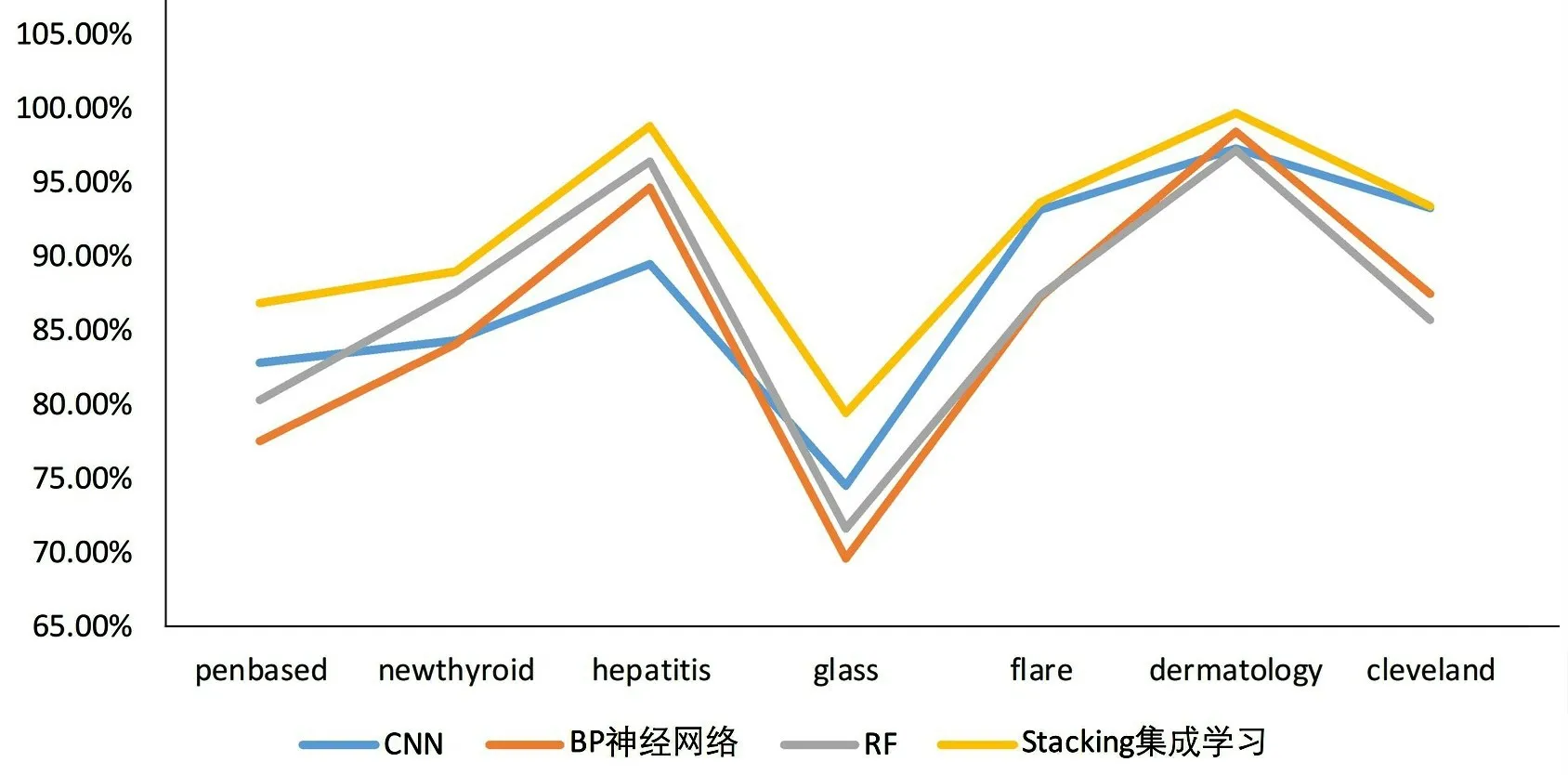
图3 各模型预判准确率对比Fig.3 Comparison of prediction accuracy of models
从图3 中可以看出,本文所构建的Stacking 集成学习模型在7种数据集样本中的预判准确率均获得了较好的效果。相比于CNN、BP 神经网络以及RF,Stacking集成学习模型能够更好地识别数据集样本的类型,这也意味着其能够在故障预判中获取更高的准确率和更好的预判效果。
为验证本文所提出基于Stacking集成学习的飞行模拟器设备故障预判方法的实际效果,根据专家经验及日常故障维护记录,构建飞行模拟器故障数据集样本如表4所示。
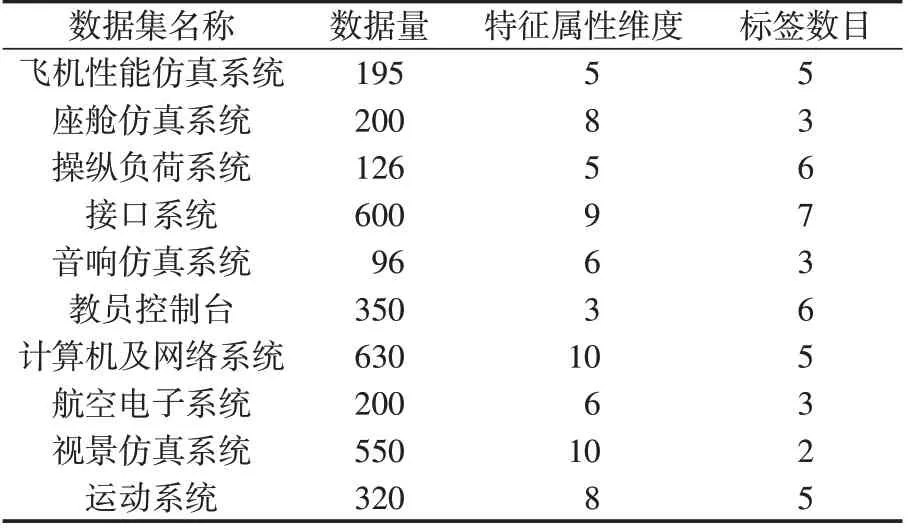
表4 飞行模拟器数据集样本信息Tab.4 Sample information of flight simulator data set
基于Stacking集成学习的飞行模拟器设备故障预判方法的准确率如图4 所示。可以看出,飞行模拟器故障特征较为明显,因而基于Stacking 集成学习的飞行模拟器设备故障预判准确率非常高。对于已经训练的数据,均可以正确预判;对于非训练数据,则存在一定的误差(误差在允许范围之内)。
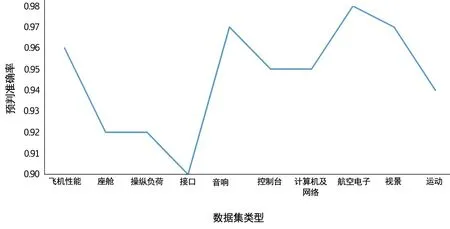
图4 飞行模拟器设备故障预判准确率Fig.4 Prediction accuracy of flight simulator equipment failure
4 结论
本文通过开展特征工程和建立Stacking集成学习模型两大步骤,提出了1 种基于数据驱动的智能设备故障预判方法。该方法首先采用正态分布法和箱型图法对原始的数据集样本进行缺失值填补和异常值处理;进一步使用KPCA对数据集进行特征提出和降维处理,并基于CNN、BP神经网络以及RF这3种典型的机器学习方法,构建了Stacking 集成学习模型。在此基础上,对数据集的样本类型作出判断。
算例结果表明,所构建的Stacking 集成学习模型较好地融合了3 种基分类器的优势,能够获得相对较高的预判准确率。同时可以看出,CNN、BP神经网络和RF 这3 种基分类器对于数据集样本的数量和维度都具有较高的敏感性,当数据量较低或者数据维度较高时,基分类器会出现预判精度不足的问题,而Stacking集成学习模型则弥补了这一缺陷。
受数据集样本数目及种类的影响,本文所提方法仅在相对理想的公共数据集上作了有效性论证,后续将会在实际的飞行模拟器设备故障数据集上作进一步的研究和论证。

