基于Wiener过程的弹用电连接器温湿应力加速建模
姜普涛,韩建立,吴一乔
(1.海军航空大学,山东 烟台 264001;2.91423部队,辽宁 大连 116041)
0 引言
在导弹长期贮存过程中,弹用电连接器的性能会随着时间推移而缓慢退化,当性能退化累积到规定阈值时就会发生失效,进而影响导弹的可靠性和安全性[1]。为了能够准确地对弹用电连接器可靠性进行评估,通常需要结合导弹实际服役环境和电连接器的失效物理过程,充分分析确定影响电连接器性能退化的主要因素。传统的基于单、多应力或组合应力下失效物理的建模方法,往往只是通过对模型参数赋予修正因子,以消除不确定因素带来的影响,没有完全体现电连接器在特定环境下的真实退化过程。Wiener 过程由于充分考虑了随机性因素,能够较好地反映产品的实际退化状态,因此被广泛应用于产品性能退化过程的建模[2]。
Tsai T R等以发光二级管的流明作为产品的性能指标,使用线性Wiener过程描述了发光二极管的性能退化轨迹[3];孙旭波等综合利用Wiener 过程和Arrhenius 加速模型建立了某电连接器温度应力可靠性模型,为提高模型参数的估计精度,采用极大似然法对所有性能退化数据进行整体统计推断[4];王玺等基于非线性Wiener过程,提出了1 种解决航空发动机性能退化非线性和三源波动问题的剩余使用寿命(Remaining Useful Life,RUL)评估方法[5];南西康等以液压系统的柱塞泵为研究对象,使用Wiener过程模型描述了其剩余寿命的分布规律[6];盖炳良等为确定某引信橡胶圈加速退化试验中性能参数和温度应力的关系,基于加速因子不变原则推导了Wiener退化模型中漂移系数和扩散系数的比例关系[7]。
目前的导弹延寿工程实践中,电连接器可靠性建模大都没有在其贮存周期的全部阶段对湿度予以充分考虑。然而,深入分析临近贮存期的某型导弹的实际服役环境后,明确湿度对该弹用电连接器贮存寿命的影响,尤其在湿度较高时,是不可忽视的。在对电连接器失效物理分析的过程中发现,电连接器的性能退化存在诸多随机性因素。因此,本文基于Wiener过程建立了某型弹用电连接器接触电阻温湿应力下的性能退化模型,并通过相关实例的加速退化数据对模型合理性进行了比对验证。
1 Wiener过程
设t 时刻样品的性能退化量为y( t ),如果y( t )在连续时间的随机过程中满足下列条件,则y( t )为Wiener过程。
1)Δy( t )为时刻t~(t+Δt )内退化量的增量,且服从正态分布,即:
Wiener过程增量的分布只与时间差有关,所以它是齐次的独立增量过程,服从正态分布。
2)在任意不相交的时间段[t1,t2] 、[t3,t4] 内,t1<t2≤t3<t4,增量y( t2)-y( t1) 与y( t4)-y( t3)相互独立。
3)y( 0 )=0,且y( t )在t=0 处连续。
一元线性Wiener过程可描述为:
若C( t )为时间t 的函数,且C( 0 )=0,文献[8-9]提出了1种性能退化的非线性Wiener过程,即:
式(3)中:μ 为漂移系数;σ 为扩散系数;W( t )为标准的Wiener过程。
2 基于Wiener 过程的电连接器接触电阻温湿应力性能退化建模
2.1 基于Wiener过程的接触电阻性能退化模型
电连接器在贮存环境应力的长期作用下,其接触电阻性能会随时间的推移而产生退化。设在t 时刻电连接器接触电阻性能退化量为y( t ),在t1时刻的性能退化量为y( t1),在t2时刻的性能退化量为y( t2)。令t1<t2,则在Δt=t2-t1时间段内的性能退化增量为Δy=y( t2)-y( t1) ,即接触电阻的增长量。
在接触电阻性能退化过程中,接触电阻的增长是由接触斑点多次氧化腐蚀和微动磨损产生的氧化物膜层堆积造成的,这些细微氧化物造成的接触电阻损失量的不断累积,直接成了接触电阻增长量的来源。从微观层面上看,在Δt 时间段内,接触电阻的增长量Δy 是由多个微小的、相互独立的损失量积累而成,即Δy 是大量符合独立同分布的随机变量之和。根据中心极限定理,在Δt 时间间隔内,当这些微小的随机变量数量足够巨大时,Δy 服从正态分布,即:
式(4)中,μΔy和分别是随机变量Δy 的均值和方差。
根据摸底试验,对于电连接器而言,其接触电阻性能退化量y( t )的整体趋势是递增的,但在一定的时间段Δt 内,其退化增量Δy 有时为正、有时为负,符合上述正态分布特点。考虑Wiener过程的特点,使用非线性Wiener 过程来描述电连接器接触电阻性能退化过程,令时间尺度函数C( t )=tb,则接触电阻Wiener过程退化模型可表示为:
式(5)中:r( t )为t 时刻接触电阻的阻值;r0为接触电阻初始值;μSk和σSk分别为环境应力Sk下Wiener 过程退化模型的漂移系数和扩散系数,且接触电阻的退化增量Δy~N();b 为时间尺度函数的待估参数。
2.2 基于Wiener过程的电连接器寿命分布模型
若给定试验样品电连接器的失效阈值,用l 来表示,则电连接器的寿命即接触电阻性能退化量y( t )首次达到失效阈值l 的时间。令随机变量ξ 表示电连接器寿命,则有:
对于基于Wiener过程的产品性能退化模型,如果漂移系数随时间呈非线性时,即模型中的时间尺度函数为非线性函数,通常来说,其寿命分布函数的精确表达式是难以获得的。为了解决此类问题,本文结合文献[10]给出的产品首次达到失效阈值时间的逆高斯分布和式(5),设RSk( t )、FSk( t )和fSk( t )分别表示电连接器在应力Sk下寿命ξ 的可靠度函数、累计失效概率函数和概率密度函数,推导得到:
式(7)(8)中:l 为接触电阻失效阈值;Φ()· 为标准正态函数。
对式(8)两边进行求导,可得:
若令ξb表示为时间tb的随机变量,则随机变量ξb的平均值可以通过对式(9)求期望得到:
则电连接器在应力Sk作用下的平均寿命可约等于:
2.3 基于Wiener 过程的电连接器温湿应力加速退化建模
通过加速试验对产品可靠性进行评估时,为了能够利用寿命分布模型实现对产品评估预测,需要建立反映产品性能表征量与加速应力之间关系的加速方程式[11]。然而,在对加速试验数据开展统计分析阶段,往往由于待估参数较多而增加了计算的难度,在多应力加速试验的情况下数据统计尤为复杂。因此,为评估弹用电连接器的可靠性,本文基于加速因子不变原则,对经典的两应力Peck 加速模型进行了简化变换,建立了基于Wiener 过程模型的电连接器温湿应力加速模型。
1)基于加速因子不变的Wiener 过程退化模型参数分析。
在加速试验中,令Sk表示第k 组加速应力水平,k=1,2,…,K ,K 为加速试验的应力组数,FSk( t )表示产品在t 时刻的累积失效概率,且FSk( 0 )=1。假设当应力水平S1和应力水平S2下分别作用时间t1和t2后,产品的累积失效概率仍然一样,即FS1( t1) =FS2( t2),则可将S1对S2的加速因子AFS1,S2定义为:
为了使产品在不同应力作用下的失效机理保持一致,必须保证加速因子保持不变,二者是充要条件,即加速因子AFS1,S2是1个只由应力S1和S2决定,并不随时间t1和t2而改变的常数[12-13]。因此,结合式(12),应力S1和S2下的产品累积失效概率函数关系可表示为:
通过对式(13)两边进行求导,可得概率密度函数之间关系为:
将式(9)电连接器接触电阻在应力Sk下的概率密度函数表达式代入式(14),并进行推导可得:
由于AFS1,S2与时间无关,则式(15)中=1,故b=b2=b1,因此可简化为:
为保证AFS1,S2与时间无关,令式(16)中的时间系数为0,则有:
继续对式(17)推导求解,最后得到:
基于上述分析可得:电连接器Wiener过程退化模型中的漂移系数μSk和扩散系数σSk满足关系式而时间尺度函数中的待估参数b 可看作常量。
2)温湿应力下Wiener 过程退化模型参数的加速方程。
由于产品退化速率在不同应力水平下会发生变化,为量化电连接器性能退化表征参数在不同温湿应力水平下的变化情况,本文采用两应力Peck模型[14]来描述电连接器Wiener 过程性能退化模型中漂移系数μSk和扩散系数σSk与温度T 、相对湿度RH 之间的关系:
式(19)中:A(T,RH)表示反应速率;a0、b0和c0为与产品材料等有关的参数;T 为热力学温度;RH 为相对湿度。上式两边分别取对数可得:
令a1=lna0,b1=-b0,假设Sk表示第k 组温湿应力组合(Tk,RHk),对上式进行线性化处理后,可得:
结合文献[15],Wiener 过程退化模型中的漂移系数和扩散系数可表示为:
式(22)中,a11、b11、c11、a12、b12和c12为中间变换量。
如需满足式(18)中的比例关系,对式(22)推导可得:b11=2b12,c11=2c12。
进一步,令γ1=a11、γ2=b11、γ3=c11、γ4=a12,于是可得温湿应力下Sk下电连接器接触电阻性能退化的加速模型,表达为:
式(23)中,γ1、γ2、γ3和γ4为待估参数。
3 基于两步极大似然法的参数评估方法
设电连接器在第k 组温湿加速应力Sk下第j 个产品第i 次测量时刻为tijk,性能退化量为y( tijk),时间增量为 Δtijk=tijk-t(i-1)jk,性能退化增量为Δy( tijk)=y( tijk)-y(t(i-1)jk)。 式 中 : k=1,2,…,K ;j=1,2,…,Mk;i=1,2,…,N ;K 、Mk和N 分别为加速试验的应力组数、第k 组应力下的试验样品数和性能退化测量的总次数。
结合式(4)(5)可知Δy( tijk)~N(μSkΔtijk,σSk2Δtijk)。不考虑电连接器个体之间的差异[16],令τ=C( t )=tb,经时间尺度模型变换后,电连接器的性能退化数据[t,y( t )]可变换为[τ,Δy′( τ )],因此有:
式(24)中,
上述Δτijk为经过时间尺度变换后应力Sk下第j个产品第i 次测量的时间增量。 y′( τijk)和Δy′( τijk)分别为对应的性能退化量和退化增量;μSk和σSk分别为应力Sk下电连接器Wiener 过程性能退化模型的漂移系数和扩散系数。
综合式(9)(23)和(25),可建立电连接器概率密度极大似然估计函数为:
将Δy′( τijk)=Δy( tijk)代入式(26)中,可得:
式(26)(27)中,Θ={γ1,γ2,γ3,γ4,b}表示式中所有待估参数的集合,另外 τ=tb,因而有
下面,根据极大似然法模型参数估计步骤,采用链式法则进行参数估计。令式(27)中关于γ1、γ2、γ3和γ4的一阶偏导都为0,即:
经过系列计算和简化,可以得到γ1、γ2、γ3和γ4的最大似然估计分别为:
同样采用链式法则对未知参数b 做一阶偏导计算,并令求导结果为0,即:
式(30)中:
结合式(30)~(32),可以得到未知参数b 的最大似然估计。针对b 的最大似然估计的显式表达式无法得出,可以通过γ1、γ2、γ3和γ4的最大似然估计并结合试验数据间接得到。
仅从数学推导上来看,将电连接器的加速退化试验数据处理代入式(29)中,经过计算可以求解得到待估参数γ1、γ2、γ3和γ4的值,但从实际对上述方程式进行推导的过程来看,由于未知数较多,式(29)的数学求解计算非常复杂,待估参数往往难以通过这种方式直接得到。有鉴于此,本文利用MATLAB 软件,采用两步极大似然估计方法,完成对电连接器概率密度极大似然估计函数中未知参数的求解[17]。参数估计具体过程如下。
第1步:对待估参数γ1、γ2、γ3和γ4进行估计。
变量为γ1、γ2、γ3和γ4,优化函数为lnΘ,目标为函数lnΘ 值最大。
2)根据式(29),通过计算可以得到未知参数的第
1次迭代结果Θ(1)=();
4 实例验证分析
使用文献[18]的试验数据,失效阈值l=5,采用本文方法,利用MATLAB采用两步极大似然估计方法计算,得到模型参数估计值,并根据加速因子比例关系式得到正常应力水平下Wiener 加速模型的漂移系数和扩散系数的估计值。全部参数估计值如表1所示。
将上述参数估计值代入式(7)(9),可得接触电阻在应力S0下寿命分布的可靠度函数为:
概率密度函数为:
由式(11)计算可得,正常应力水平下的平均寿命为:
图1、2 分别描绘了本文利用Peck 加速模型和文献利用广义Eyring 加速模型下得到的可靠度和概率密度函数曲线。

图1 可靠度曲线比对图Fig.1 Comparison of reliability curves
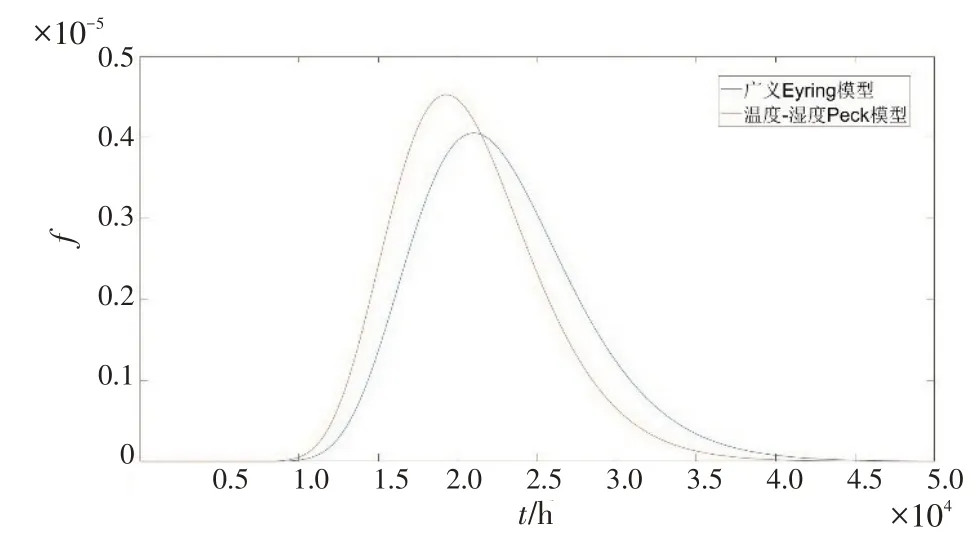
图2 概率密度函数曲线比对图Fig.2 Comparison of probability density curves
从对比图可以看出,2 种方法得到的曲线基本吻合。对比文献得到的平均寿命值2.265×104h,本文在参数估计时考虑了Wiener 模型扩散系数及时间函数的非线性因素,所得平均寿命更为保守一些,从追求可靠性角度来看,本文采用的方法更为安全可靠。
5 结论
本文考虑了某型弹用电连接器服役地域的特殊性和性能退化过程中的随机因素特点,建立了该弹用电连接器基于加速退化数据的温湿应力Wiener 性能退化模型,并给出了参数评估方法。主要结论如下:
1)采用两应力Peck 加速模型来描述温度和湿度对电连接器性能变化的影响时,在考虑其Wiener退化模型扩散系数与应力有关的情况下,能够得到更为安全可靠的平均寿命值;
2)利用加速因子不变原则很好地简化了加速模型中待估参数的数量,大大降低了模型参数估计的复杂度;
3)对于待估参数显性表达式难以通过数学推导直接得到的问题,可以利用MATLAB,通过两步极大似然估计方法,采用链式法则予以解决。

