基于自适应趋近律的对称六相PMSM调速系统
刘陵顺,李永恒,葛宝川
(1.海军航空大学,山东 烟台 264001;2.92781部队,海南 三亚 572029)
0 引言
传统PI 控制策略无法摆脱对电机模型和参数的依赖,难以满足舰船、飞行器等军事装备对电机高性能控制算法的要求,因而具有一定的局限性。为提高电机控制性能,国内外学者提出诸多高性能控制算法[1]。其中,滑模变结构控制算法对外部干扰及内部参数变化具有不敏感性和极好的鲁棒性,控制算法简单,动态性能优异,能够较好地满足军事装备对电机高性能控制算法的要求。此外,它还具备动态响应速度快、谐波含量低、滑动模态下自适应性强、稳定范围宽等优点。
这种算法自身也存在缺点。在理想状态下,电机控制系统在结构控制力度无限强、切换频率无限大时不会产生抖振。但实际情况下,受到切换开关不理想以及各种动作延迟等因素影响,系统切换频率无法达到无限大,导致电机控制系统产生抖振。高为炳为克服滑模运动抖振问题,提出指数趋近律方法。通过调节趋近律参数,增强电机控制系统动态性能,减小抖振,但指数趋近律方法无法从根本上消除系统抖振[2-6]。
本文提出1种适用于九开关变换器驱动的对称六相PMSM 调速系统的基于自适应趋近律的滑模控制方法,以此来进一步提高系统响应速度和抑制系统抖振问题。该自适应趋近律综合幂次趋近律和变速趋近律优点,随着系统状态变量自适应调节滑模面参数,直至系统状态轨迹运行到稳定点。当系统出现有界外部干扰时,系统状态及其导数可快速收敛到平衡点附近的邻域内。
1 基于自适应趋近律的对称六相PMSM 调速控制器设计
1.1 对称六相PMSM数学模型
对称六相PMSM 物理模型中的转子结构为表贴式,每相绕组的相位两两互差60°,其转子物理模型结构如图1所示[7]。
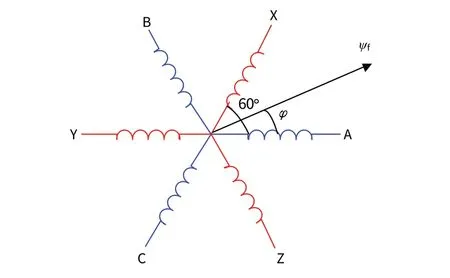
图1 对称六相PMSM电机结构图Fig.1 Structure of symmetrical six-phase PMSM
为了满足本文研究需要,作出如下假设:
1)对称六相PMSM 电机转子结构上没有阻尼绕组;
2)研究过程中忽略定子、转子铁心磁阻;
3)研究过程中不考虑磁滞损耗和涡流损耗;
4)励磁磁场和电枢反应磁场在气隙中都是按照正弦规律分布的。
本文采用id=0 的转子磁场定向控制策略,建立对称六相PMSM 电机在dq 坐标系中的电机数学模型,可得对称六相PMSM定子电压方程为:
式(1)中:ud、uq为d、q 轴上的电压分量;id、iq为d、q 轴上的电流分量;Rs为定子电阻;Ld、Lq为d、q 轴定子电感;ωe为转子电角速度;ψf为转子磁链。
本文采用磁场定向控制策略,即id=0,此时d、q坐标系下的电磁转矩表达式为:
式(2)中:Te为电机电磁转矩;p 为电机的极对数。
电机数学模型中的运动方程为:
式(3)中:TL为负载转矩;J 为转动惯量;ωm为转子机械角速度;B 为阻尼系数。
将式(2)(3)联立可得电机数学模型中的机械运动方程为:
1.2 控制器设计
设计滑模控制器的首要步骤在于寻找合适的滑模面;然后,在滑模面的基础上设计控制器。
根据式(4),设计电机调速系统二阶状态空间方程为:
式(5)中:系统状态变量x1=ωref-ωm,ωref为电机参考机械角速度;系统状态变量x2=x˙1=-ω˙m;控制作用u=i˙q。理想条件下,一般认为负载转矩TL为恒定值,即T˙L=0。但在实际应用PMSM时,负载转矩TL是不断变化的,尤其在负载突变时,不能简单地把负载转矩TL认定是恒值。
对于滑模控制器来说,线性滑模面是最常用的几种滑模面之一。设计线性滑模面:
式(6)中:s 为线性滑模面函数;c 为滑模面比例系数。对式(6)进行求导,可得:
将式(7)整理,可得控制作用u 为:
对式(8)等式两端分别求积分,可得:
在幂次趋近律[8-10]和变速趋近律[11]基础上,提出了1种自适应趋近律[12]:
式(10)中:k1>0 ;α >0 ;ε′=k2tansig |x |,k2>0 ,
将式(10)代入式(9),得:
系统控制器输出包含积分环节,可以消除稳态误差,提高系统精度。但采用式(6)的线性滑模面,系统容易受到负载转矩突变的影响。根据式(5),当负载转矩TL突变时,负载转矩变化量T˙L突变为较大值,进而影响调速系统二阶状态空间方程的稳定性,不利于控制器设计。
基于上述原因,设计积分滑模面:
对式(12)进行求导,可得:
将式(13)整理,可得控制器输出iq为:
将式(10)代入式(14),得:
式(15)为基于自适应趋近律的对称六相PMSM调速系统控制器输出。iq作为电机q 轴电流控制器输入的给定值,电机实际电流通过跟踪控制器输入给定值,进而输出q 轴电压uq。
设计q 轴电流控制器积分滑模面为:
式(16)中,eq=iq-iq1,iq1是电机定子六个相电流按照矢量空间解耦变换的q 轴上的电流分量,c1>0。
对式(16)求导,并将式(1)代入,可得:
将式(10)代入式(17),可得:
由式(18)可以求得电流控制器q 轴上的输出电压为:
同理,设计d 轴电流控制器积分滑模面为:
式(20)中,ed=-id1,id1为电机定子的六个相电流按照矢量空间解耦变换的d 轴上电流分量,c2>0。
对式(20)求导,并将式(1)代入求导后的式(20),可得:
将式(10)代入式(21),得:
由式(22)可以求得电流控制器d 轴上的输出电压为:
式(23)(19)分别为电流控制器d、q 轴上的输出电压。将电流控制器d 、q 轴输出电压由dq 变换到αβ 坐标系,可得α、β 轴电压。
2 仿真结果分析
图2为本文研究的九开关变换器的拓扑结构。九开关变换器的结构包含3 个桥臂,每个桥臂包含3 个IGBT开关管,共有9个开关管(S1~S9)。
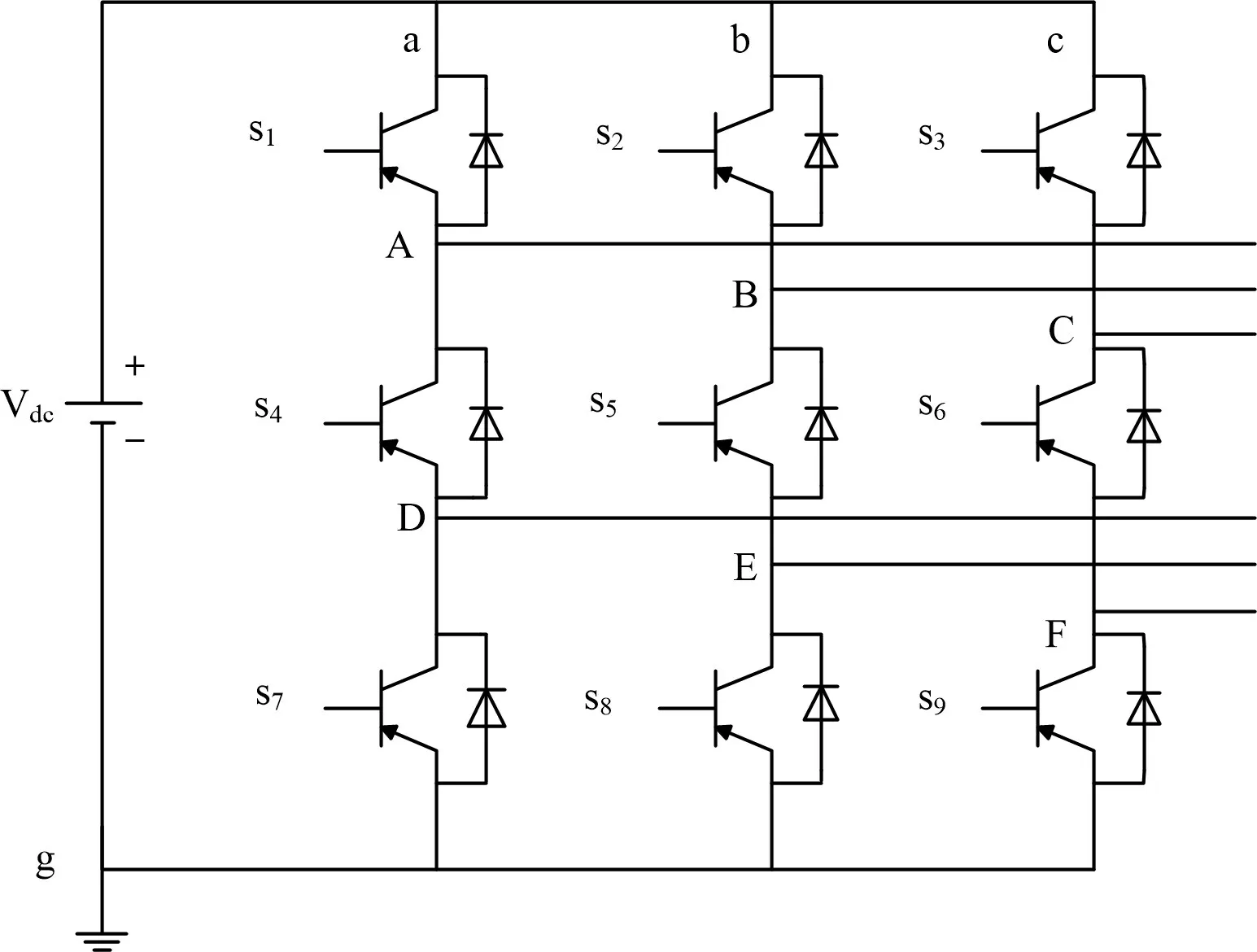
图2 九开关变换器拓扑结构Fig.2 Nine-switch converter topology
其中:S1、S2、S3为上侧开关管;S4、S5、S6为中间开关管;S7、S8、S9为下侧开关管。上侧开关管和中间开关管组成上侧换流器;中间开关管和下侧开关管组成下侧换流器。九开关变换器对中间开关管进行了复用,能够减少开关数量,减轻变换器的质量和缩小变换器的体积[13-15]。
中间开关管的通断是由上、下侧开关管决定的,并且上、下侧开关管的通断满足异或关系:即上侧开关管工作时,中间开关管工作,下侧开关管不工作,此时,九开关变换器的上侧换流器工作,下侧换流器不工作;下侧开关管工作时,中间开关管工作,上侧开关管不工作,此时,九开关变换器的下侧换流器工作,上侧换流器不工作。为了满足直流母线电压不能短路的条件,有效的开关信号仅有3种,本文以a桥臂为例进行情况说明,如表1 所示。研究过程中不考虑开关的死区。本文以a桥臂来说明开关状态与输出电压的情况:上侧开关管S1和中间开关管S4的导通与断开共同决定电压UAg;中间开关管S4和下侧开关管S7的导通与断开共同决定电压UDg。
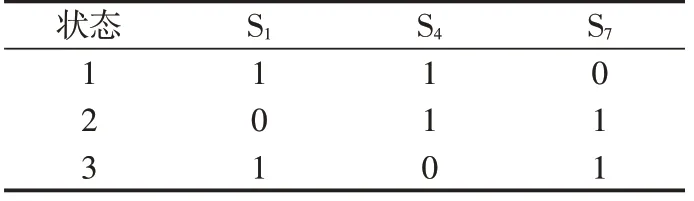
表1 九开关变换器a桥臂开关状态Tab.1 A-phase bridge arm switch status of nine-switch converter
为了验证基于自适应趋近律的对称六相PMSM调速系统有效性,在MATLAB/Simulink平台搭建电机驱动模型,如图3 所示。对称六相PMSM 的电参数如下所示:定子电阻Rs=1 Ω,定子漏感Ld=4.6 mH,转子磁链Ψf=0.1 Wb,转动惯量J=0.02 g·m2,极对数p=2 ,负载转矩TL=1 N·m ,直流侧母线电压Vdc=300 V。
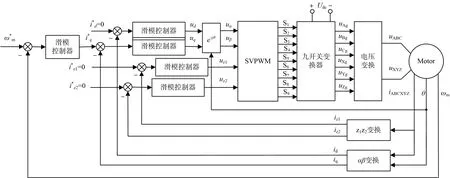
图3 电机调速系统框图Fig.3 Block diagram of motor speed control system
将基于自适应趋近律电机调速系统与基于指数趋近律电机调速系统[16-18]进行比较,可得系统启动后的转速、电磁转矩、电流iq以及A 相电流波形,如图4所示。系统启动后的电压uα、uβ以及电流iα、iβ波形如图5 所示。其中,滑模面参数c=5,指数趋近律参数k=10,ε=5,自适应趋近律参数k1=10,k2=5,α=1.2。
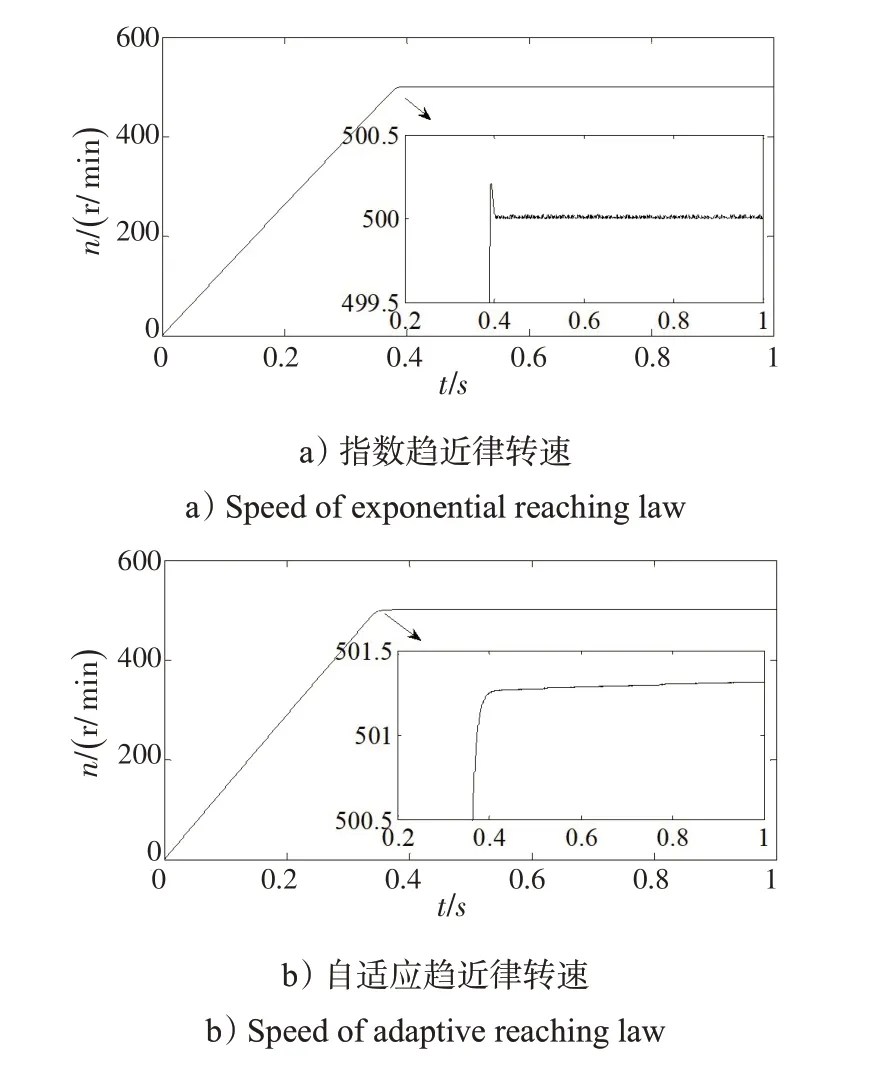
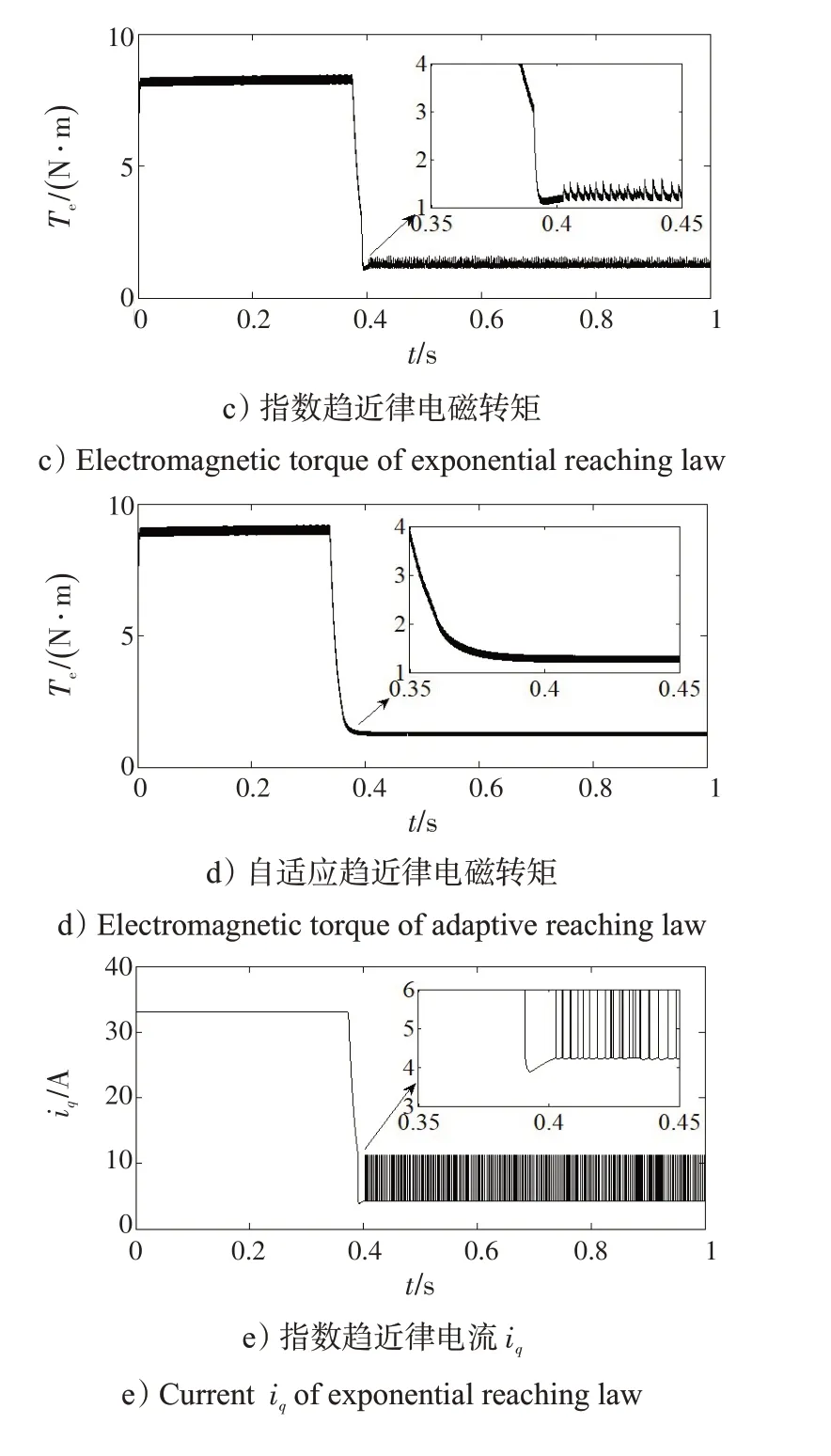
图4 电机转速、电磁转矩、电流iq 以及A相电流波形比较Fig.4 Waveform comparison of motor speed,electromagnetic torque,current iq and A-phase current
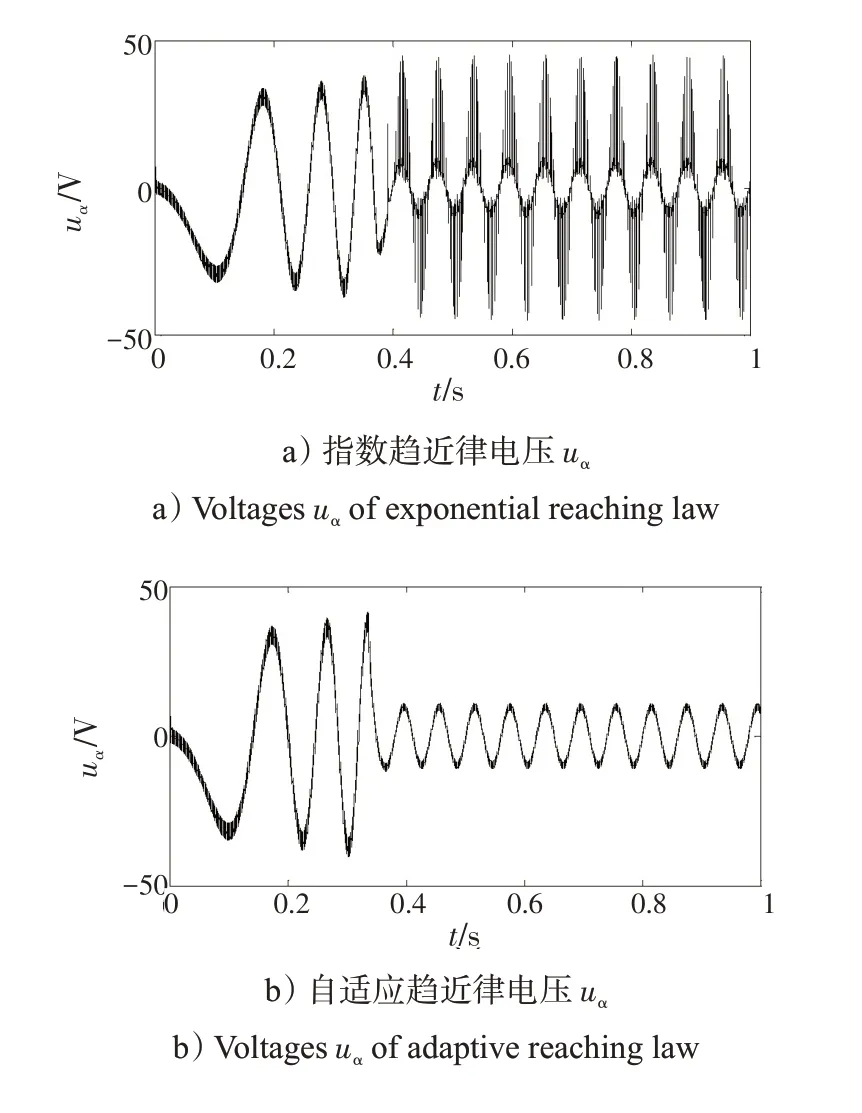
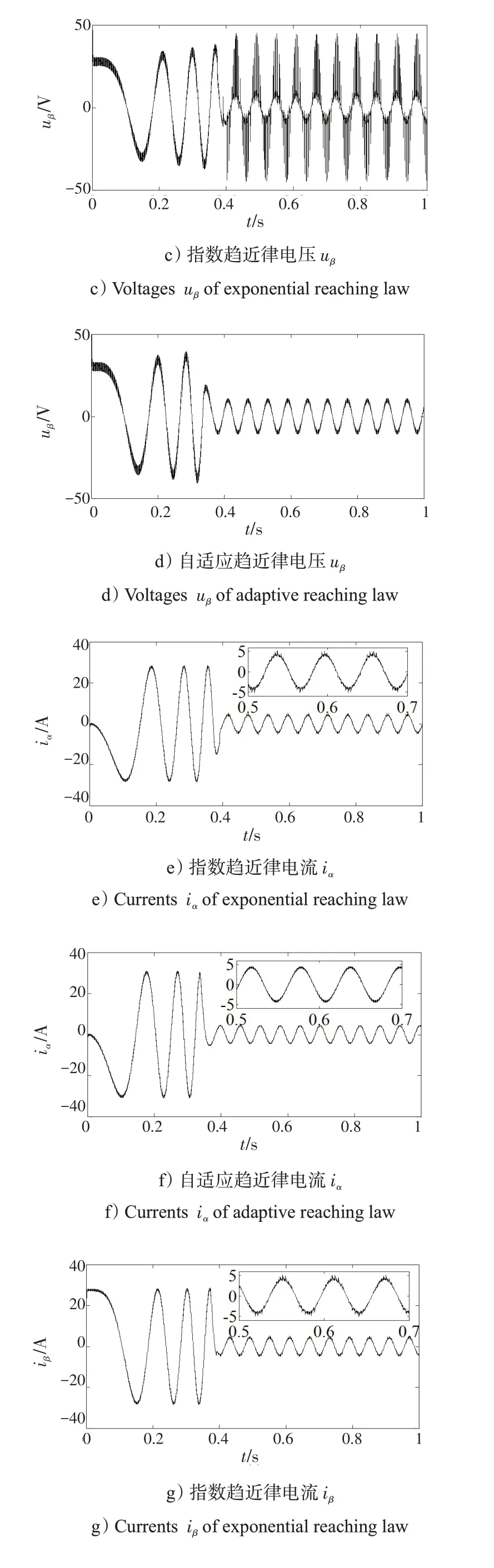
图5 电机电压uα、uβ 以及电流iα、iβ 波形比较Fig.5 Waveform comparison of motor voltages uα,uβ and currents iα,iβ
从图4 可以看出,指数趋近律控制系统转速动态调节时间较长,超调量较大,且到达稳态后转速波动较大。电磁转矩、电流iq超调量较大,且到达稳态后波动较大。A相电流稳态精度略显不足。
自适应趋近律控制系统转速动态调节时间短,超调量小,稳态性能良好。电磁转矩、电流iq超调量较小,到达稳态时过渡光滑,波动较小。A相电流稳态性能良好。
从图5 可以看出,指数趋近律控制系统电压uα、uβ波动很大,导致电流iα、iβ稳态性能不足。而自适应趋近律控制系统电压uα、uβ波动较小,电流iα、iβ稳态性能良好,这说明了电机具有良好的电磁转矩和转速。
3 结论
本文针对基于九开关变换器的对称六相PMSM调速系统,提出了1 种基于自适应趋近律的滑模控制方法,建立对称六相PMSM 调速系统数学模型,并将自适应趋近律控制方法应用于电机调速系统。仿真结果表明,相比于指数趋近律,自适应趋近律滑模控制方法能够有效提高调速系统动态性能和稳态精度。

