双基地角时变下的ISAR等效旋转中心估计

郭宝锋，孙慧贤，胡文华,*，尹文龙，陈关军

1. 陆军工程大学石家庄校区 电子与光学工程系，石家庄 050003 2. 中国人民解放军32136部队，张家口 075000

双基地雷达是发射机和接收机分置、且基线长度与目标距离可比拟的雷达系统，收发分置的工作方式使雷达在对抗“四大威胁”方面具有突出的优势[1]。双基地逆合成孔径雷达[2-3]是基于双基地雷达平台的逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)系统，在具备“四抗”特性的同时，利用接收的目标非后向散射回波进行成像，能够较单基地雷达获取更加丰富的目标信息[4-6]。为此，双(多)基地雷达系统日益成为现代雷达研究的热点问题[7-11]。距离-多普勒(Range-Doppler, RD)算法[12-13]是双基地ISAR成像的经典算法，由于其物理意义明确、操作简便被广泛应用于成像仿真及实测数据的处理中，但当观测目标尺寸过大或成像累积转角过大时，该算法存在越分辨单元徙动问题[14-15]，造成图像散焦，离旋转中心越远，散射点散焦现象越严重。为了完成越分辨单元徙动的校正从而提高成像质量，需要估计目标的等效旋转中心。

目标等效旋转中心估计可由基于单特显点的运动补偿算法近似得到，但该算法得到的旋转中心位置精度较低，影响后续图像校正的聚焦效果，并且，不是所有的图像都有理想的单特显点单元[13]，尤其是实测数据中，回波信噪比一般很低，难以找到单一的特显点，因此，该算法的应用受到很大的限制。针对平动补偿不能提供等效旋转中心的情况，清华大学的叶春茂等[16-17]针对单基地ISAR旋转中心估计问题，提出了利用3个散射点在两幅图像中的位置差提取旋转中心的算法，但由于双基地ISAR成像时，双基地角变化会引起图像畸变[18]，使得该算法无法适用于双基地ISAR，文献[19]利用相似原理实现了等效旋转中心估计，但未考虑双基地角的变化，也使得算法应用范畴受限。文献[20]考虑到双基地ISAR的畸变特性，基于图像对比度最大准则估计了图像的等效旋转中心位置，该估计算法采用搜索方式，每搜索一个距离点都需要构造补偿相位项，并作快速傅里叶变换(Fast Fourier Transform, FFT)变换完成成像，运算量很大，并且等效旋转中心估计精度受限于所构造补偿相位的精确程度。

基于此，本文针对双基地角时变下的ISAR等效旋转中心估计问题，提出了一种等效旋转中心估计算法。首先，建立了双基地ISAR成像模型，分析了双基地ISAR成像特性，并推导了图像畸变角度的表达式；然后，提出了等效旋转中心估计算法，该算法将运动补偿后脉冲压缩数据分成两组成像，并进行畸变校正，通过图像旋转相关搜索等效旋转中心位置；最后，进行了仿真实验，验证了算法有效性。

1 双基地ISAR成像模型

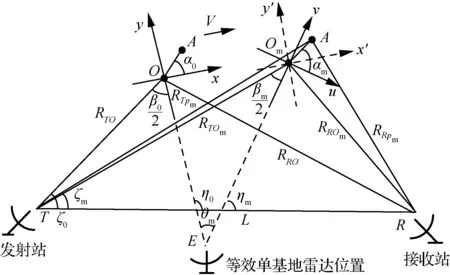
图1 双基地ISAR成像模型Fig.1 Imaging model for bistatic ISAR

由于雷达本身具有精确的测距能力，RTOm、RROm、L等距离信息可通过雷达获得，则双基地角β0、βm及ζ0、ζm的值可由三角形关系得到

(1)

(2)

(3)

(4)

(5)

(6)

此时累积转角θm为

θm=η0-ηm

(7)

假设收发双站雷达理想同步，发射站雷达以脉冲重复周期TPRT发射线性调频信号

(8)

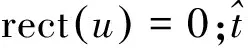
其基频信号为

(9)

设第p个散射点A的散射系数为σp，tm时刻，散射点A到收发双站的距离和为Rpm，即Rpm=RTpm+RRpm，则接收站雷达接收到的回波信号为

(10)

经过相参本振下变频至零中频，并使用匹配滤波器对目标回波进行脉冲压缩，得到散射点A的一维距离像为

(11)

双基地雷达系统中，目标尺寸远小于到收发双站距离，即d≪RTO,RRO，由于αm=θm+α0，则散射点A到发射站和接收站的距离可表示为

(12)

(13)

由式(12)和式(13)可得pm到收发双站距离和为

Rpm=(RTOm+RROm)+2(xpsinθm+

(14)

令ROm=RTOm+RROm，为目标质心到收发双站的距离和，则散射点A到收发双站距离和与目标质心到收发双站距离和之差为

(15)

经过理想的运动补偿(包括包络对齐和相位校正两个步骤)后，回波的一维距离像式(11)可表示为

(16)

假设成像期间转动角速度恒定为ω，且双基地角固定不变恒为β，由于雷达视角变化很小，累积转角可作如下近似：sinθm≈θm，cosθm≈1，且θm=ωtm。因此，式(16)可表示为

(17)

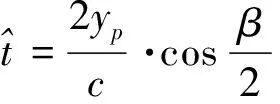
(18)

2 双基地ISAR成像特性分析

式(17)和式(18)的原理推导是在双基地角恒定及目标等效转速均匀的情况下给出的，并且累积转角作了近似，而在实际成像过程中，双基地角恒定的假设很少满足。下面推导双基地角时变情况下慢时间多普勒表示，对式(16)中的指数相位项求导可得散射点精确的瞬时多普勒信息

(19)

为便于理解，首先分析单基地情况下，令式(19)中双基地角为0，并使fd=0，可得瞬时多普勒为零的散射点的集合(即雷达观测坐标系uOmv坐标系中的纵轴)与x轴(方位向)的夹角γm为

(20)

为便于分析，单基地ISAR瞬时成像结果如图2(a)所示。

从式(20)可知，由于目标转动，成像初始时刻在y轴(距离向)上的点现在偏移了θm角度，单基地ISAR完全是散射点模型旋转后的图像显示。

对于双基地ISAR，根据式(19)，双基地角时变时，慢时间瞬时多普勒fd是方位坐标xp、距离坐标yp的复杂函数关系。成像时，瞬时多普勒为零的散射点的集合(即雷达观测坐标系uOmv坐标系中的纵轴)与x轴的夹角γm为

(21)

双基地ISAR瞬时成像结果如图2(b)所示，设多普勒为零的散射点与距离向y轴的夹角为φm，则

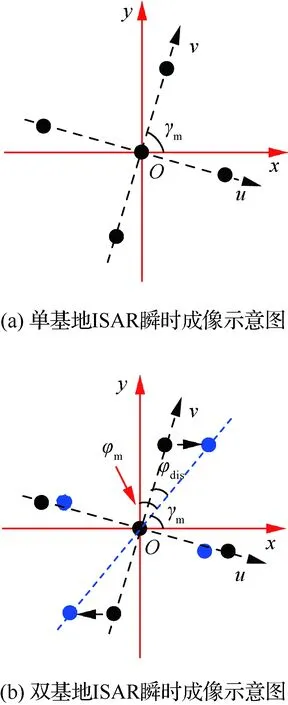
图2 单/双基地ISAR成像特性对比Fig.2 Comparison of imaging characteristics of monostatic and bistatic ISAR

(22)

以另一种形式书写式(19):

(23)

(24)

(25)

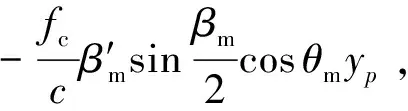
(26)

3 双基地ISAR等效旋转中心估计

根据双基地ISAR的成像特性分析，得到了图像的畸变角度，据此可以构造平移量，通过物理平移消除双基地ISAR的图像畸变，这样，图像与散射点模型之间只存在一个绕旋转中心的旋转，旋转角度由成像视角差决定。基于这个原理，本文提出基于图像旋转相关的双基地ISAR等效旋转中心估计算法，首先将成像过程按累积转角和双基地角把一维距离像序列分成两组，并分别成像，然后，对两幅图像进行畸变校正，则此时两幅图像是散射点模型旋转不同角度的显示，那么这两幅图像绕旋转中心旋转可达到最大程度的吻合，即通过图像旋转相关性最大准则对旋转中心位置进行搜索，相关性最大时对应的距离单元就是等效旋转中心位置。

3.1 图像畸变校正

假设成像期间积累脉冲个数为M，累积转角为θM，每个脉冲快时间采样点数为N，快时间采样频率为fs，畸变角度为φdis_A，平均双基地角为βA，雷达发射LFM信号的载波波长为λ，则每个距离采样单元和每个多普勒单元代表的长度为

(27)

(28)

为了消除畸变，若以第k个距离单元为基准，则第n个距离单元在方位向需要移动的数值为

Δyn=(n-k)Δytanφdis_A

(29)

对应移动的多普勒单元个数为

(30)

式中:round(·)表示对数值四舍五入取整，ΔMn>0时向左移位，ΔMn<0时向右移位。对每个距离单元按式(30)进行移位操作即可完成双基地ISAR的图像畸变校正。式(30)的取整操作会存在量化误差的问题，影响成像结果，这可通过对图像进行4～8倍插值细化，减小量化误差对成像的影响。

3.2 等效旋转中心估计

(31)

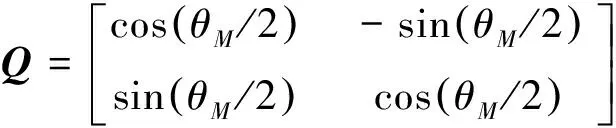
设散射点A在二维图像中的像素位置可表示为(Xp,Yp)，则坐标(xp′,yp′)与像素位置(Xp,Yp)满足如下关系

xp′=(Xp-Xc)Δx

(32)

yp′=(Yp-Yc)Δy

(33)

联合式(31)～式(33)，整理可得

(34)

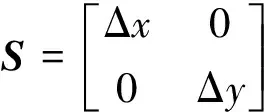
现将回波运动补偿后的数据分成两组，为尽可能减小后续的估计误差，分组后应使两组数据的多普勒分辨率相同，由于成像期间双基地角的变化，会导致两组回波脉冲个数未必相同。假设两组数据的脉冲个数分别为M1、M2，不妨设M1>M2，对两组数据分别成像，并对脉冲积累个数多的图像(M1对应的图像)以其多普勒中心进行截短，截取其中的M2个多普勒单元，使两幅图像数据维数一致，得到ISAR图像1和ISAR图像2，此时两幅图像数据维数一致。设两幅图像的累积转角分别为θM1、θM2，平均双基地角分别为βA1、βA2，由于两幅图像的方位向分辨率相同，则θM1cos(βA1/2)=θM2cos(βA2/2)，那么两幅图像的方位分辨率可表示为

(35)

距离定标因子分别为

(36)

(37)

由于两幅图像是由同一组运动补偿后的数据分组得到，因此，等效旋转中心在同一距离单元上，并且，旋转中心处多普勒值必为零，因此，两幅图像的等效旋转中心位置相同，设为(Xc,Yc)，以该中心对两幅图像进行畸变校正，消除畸变带来的方位偏移，此时两幅图像仅有一定的视角差，视角差为Δθ=(θM1+θM2)/2。

设(X1,Y1)、(X2,Y2)分别为散射点A在两幅图像中的像素位置，依照式(34)可得到散射点坐标与在图像上像素位置对应关系

(38)

(39)

根据式(38)和式(39)，散射点A在两幅ISAR图像中的像素位置关系满足

(40)

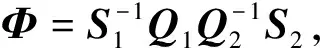
(41)

式中：Φ为两幅图像的坐标转换矩阵。式(41)表明，第1幅ISAR像的散射点相对等效旋转中心的位置可由第2幅图像相对等效旋转中心的位置经变换矩阵Φ得到。双基地ISAR的等效旋转中心在零多普勒线上，只需假定等效旋转中心的对应距离单元位置，对第2幅图通过Φ进行矩阵变换，用得到的图像与第1幅图作互相关，假设两幅图像分别记为I1和I2，其有效距离单元和多普勒单元个数分别为N和M2，则相关系数的计算公式为

(42)

当相关性最大时，该假定的旋转中心位置即为目标的等效旋转中心。需要说明的是，由于成像时相位校正一般基于强散射点的相位实现，使得等效旋转中心在散射强度较大的点附近，因此，进行距离单元搜索时，可选择图像亮度高的位置及其附近区域进行，以减小运算量。

3.3 算法运算量分析

本文算法需要对每个距离单元进行处理，包括畸变角度计算、图像畸变校正、图像旋转、图像相关等操作，这里给出算法的运算量分析。假设成像积累总脉冲个数为M，分组后两组数据的脉冲个数分别为M1、M2，令M0=min(M1,M2)，每个脉冲压缩后截取的有效距离单元个数为N，为减小运算量，等效旋转中心估计选择的距离单元搜索范围为N0，各关键步骤对应的运算量如表1所示。

从表1可以看出，图像畸变校正的移位操作的运算量较大，图像旋转会产生较多的实数乘法和实数加法运算，这两个环节占用算法主要的运算量，其次是图像相关步骤，畸变角度计算的运算量则很少。此外，运算量大小与选择的距离单元搜索范围N0直接相关，在实际操作时可根据目标的大致尺寸确定N0的大小，以最大限度减小运算量。

表1 运算量统计Table 1 Calculation statistics

4 算法流程

双基地角时变下的ISAR等效旋转中心估计流程如图3所示，具体步骤为

步骤1对双基地ISAR回波进行脉冲压缩和运动补偿，得到相位校正后的一维距离像序列。

步骤2依据累积转角和双基地角把一维距离像序列分成两组，使两组数据的多普勒分辨率一致，并分别成像得到ISAR图像1和ISAR图像2，对多普勒单元数目多的图像进行数据截短，使两幅图像的数据维数一致。

步骤3假定某一距离单元为等效旋转中心所在位置。

步骤4根据式(26)计算两幅图像的畸变角度，并通过式(30)对两幅图像进行畸变校正。

步骤5对图像2依据式(41)进行旋转，得到新的图像，并与图像1作互相关。

步骤6假设下一个距离单元为等效旋转中心位置，重复步骤4～步骤5，直至距离单元遍历结束。

步骤7根据遍历过程，寻找两幅图像相关性最大时所假定的等效旋转中心位置，该位置就是估计得到的等效旋转中心。

图3 等效旋转中心估计算法流程Fig.3 Flow chart of estimation algorithm for equivalent rotation center

5 仿真实验

为验证等效旋转中心估计算法的有效性，进行了仿真实验。仿真场景如图4所示，其中，“◇”为发射站位置，“○”为接收站位置，雷达基线长度为50 km，目标运动速度为400 m/s，目标轨道加粗部分为选择的雷达成像区域，该区域双基地角是时变的。仿真散射点模型如图5所示，仿真参数如表2所示。

首先将采集的1 024个回波进行匹配滤波完成脉冲压缩，并进行运动补偿。然后根据累积转角与双基地角关系，将1 024个脉冲压缩结果分为两组，使两组数据的多普勒分辨率相同，经计算，采用的分组方法是：第1～525个脉冲为第1组、第526～1 024个脉冲为第2组，对两组脉冲构成的一维距离像序列分别成像，得到ISAR图像1和ISAR图像2，如图6所示，这两幅图像都有一定的畸变，畸变角度理论值约为26°，向左偏移，根据图中的散射点坐标也可计算得到畸变角度为26.1°，与理论值吻合。

图4 仿真场景Fig.4 Simulation scenario

图5 散射点模型Fig.5 Scatter model

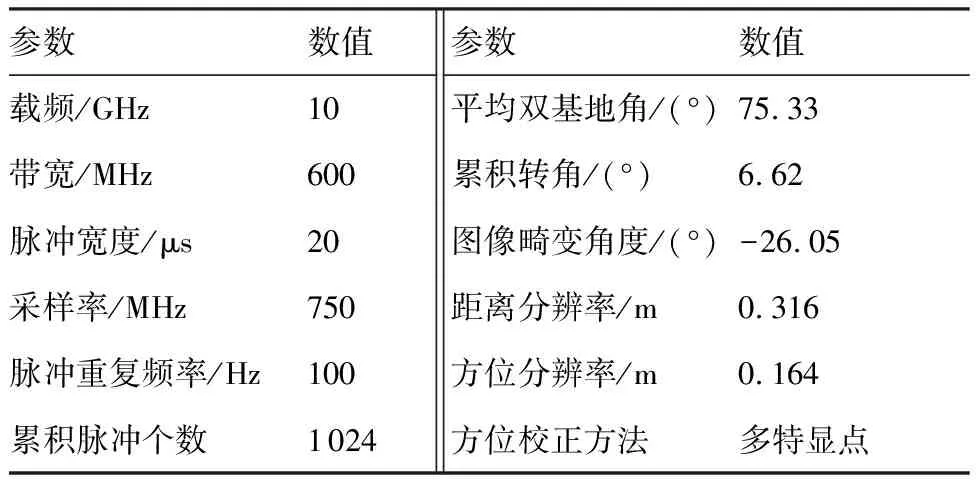
表2 成像仿真参数Table 2 Imaging simulation parameters

由于第2幅图像方位选取了499个脉冲，小于第1幅图像的525个脉冲，为了使后续的图像旋转具有相同的数据维数，将第1幅图像数据截取，保留中间的499个多普勒单元。假定等效旋转中心在某一距离单元(等效旋转中心在多普勒单元的位置为零多普勒线上，无需估计，即像素位置Xc=250)，依据畸变角度理论值，对两幅图像进行畸变校正；对第2幅图像进行旋转，并与第1幅图像作相关，存储相关系数；然后，假定下一个距离单元为旋转中心位置，再进行两幅图像的畸变校正、旋转相关，直至遍历整个距离单元。为减小运算量，本实验对目标附近的距离单元进行遍历，得到的归一化相关系数曲线如图7中实线所示，峰值点出现在第500个距离单元处，则等效旋转中心在两幅图像上的像素位置为(250,500),为验证本文算法的性能，将其与文献[19]给出的算法进行对比，文献[19]未考虑双基地角变化及图像畸变，采用该算法得到等效旋转中心搜索曲线如图7中虚线所示，峰值位置在524处，与本文算法相差24个距离单元。图8(a)和8(b)分别是ISAR图像1和ISAR图像2依据旋转中心畸变校正后的图像，此时，图像的畸变现象消除。

根据得到的等效旋转中心，采用文献[20]的越分辨单元徙动校正算法对运动补偿后的1 024个脉冲进行徙动校正，并分别成像。图9是未作校正的1 024个脉冲双基地ISAR原始成像结果，图10是越距离单元徙动校正后的ISAR像，图11(a)和11(b)分别是采用文献[19]和文献[20]的算法估计等效旋转中心并进行越分辨单元徙动校正得到的ISAR像(文献[20]算法估计旋转中心的距离单元位置为527)，图11(c)是本文算法估计旋转中心并进行越分辨单元徙动校正得到的ISAR像，对比图10和图11可以看出，图11的成像质量均优于图10，但图11(a)和图11(b)较图11(c)中散射点出现变“胖”现象，这是由于文献[19]和文献[20]的算法估计旋转中心存在误差，用该估计值未能完全校正图10的越分辨单元徙动，而本文算法适用于双基地角时变的情形，等效旋转中心估计准确，用该估计中心校正越分辨单元徙动使图像质量达到了最佳。

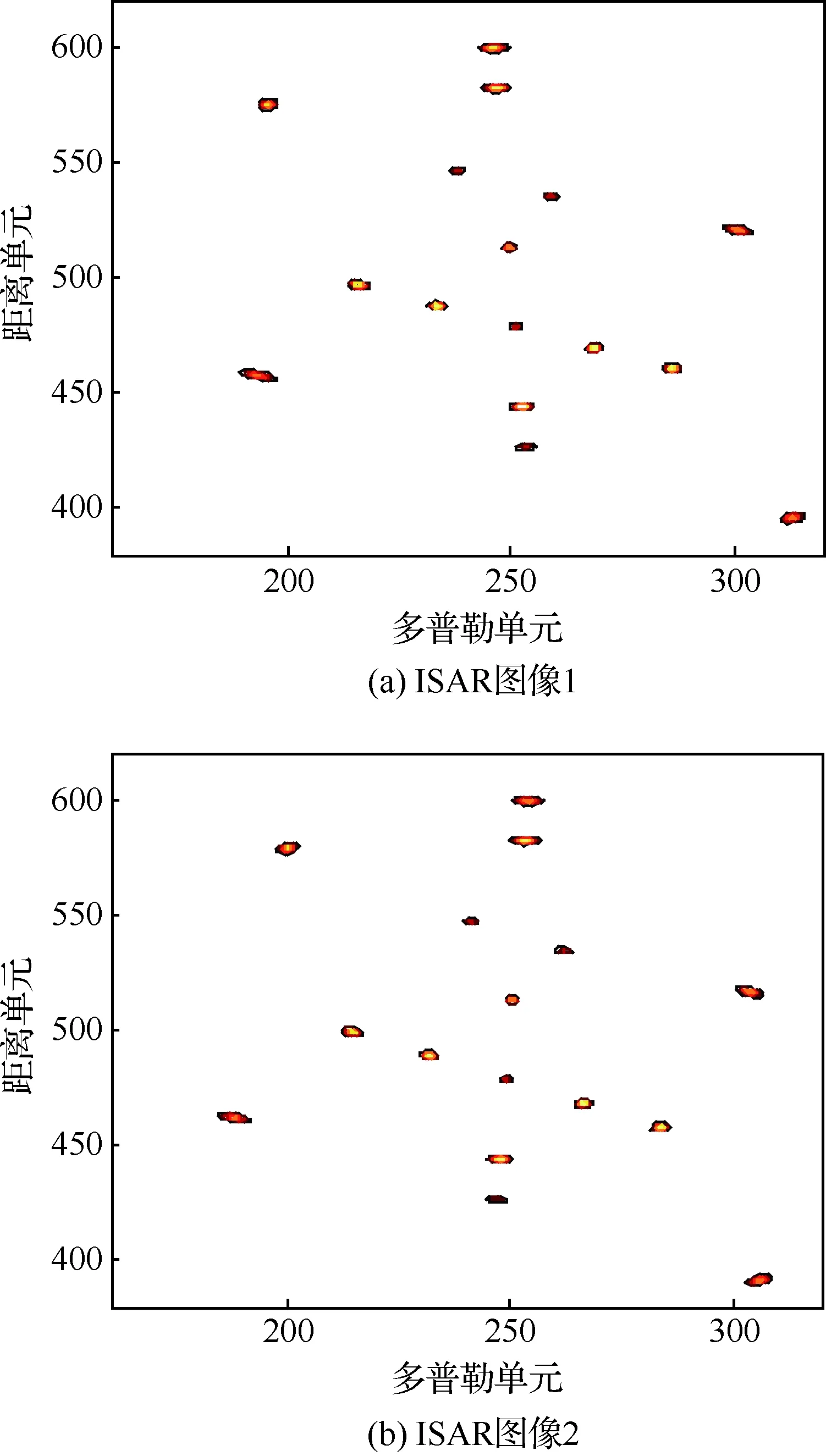
图6 分组成像结果(畸变未校正)Fig.6 Imaging results after grouping (without distortion correction)

图7 旋转中心搜索曲线Fig.7 Rotation center estimation curves

图8 分组成像结果(畸变校正后)Fig.8 Imaging results after grouping (after distortion correction)

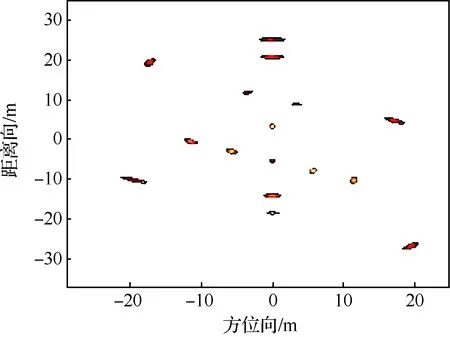
图9 双基地ISAR原始图像Fig.9 Original image of bistatic ISAR

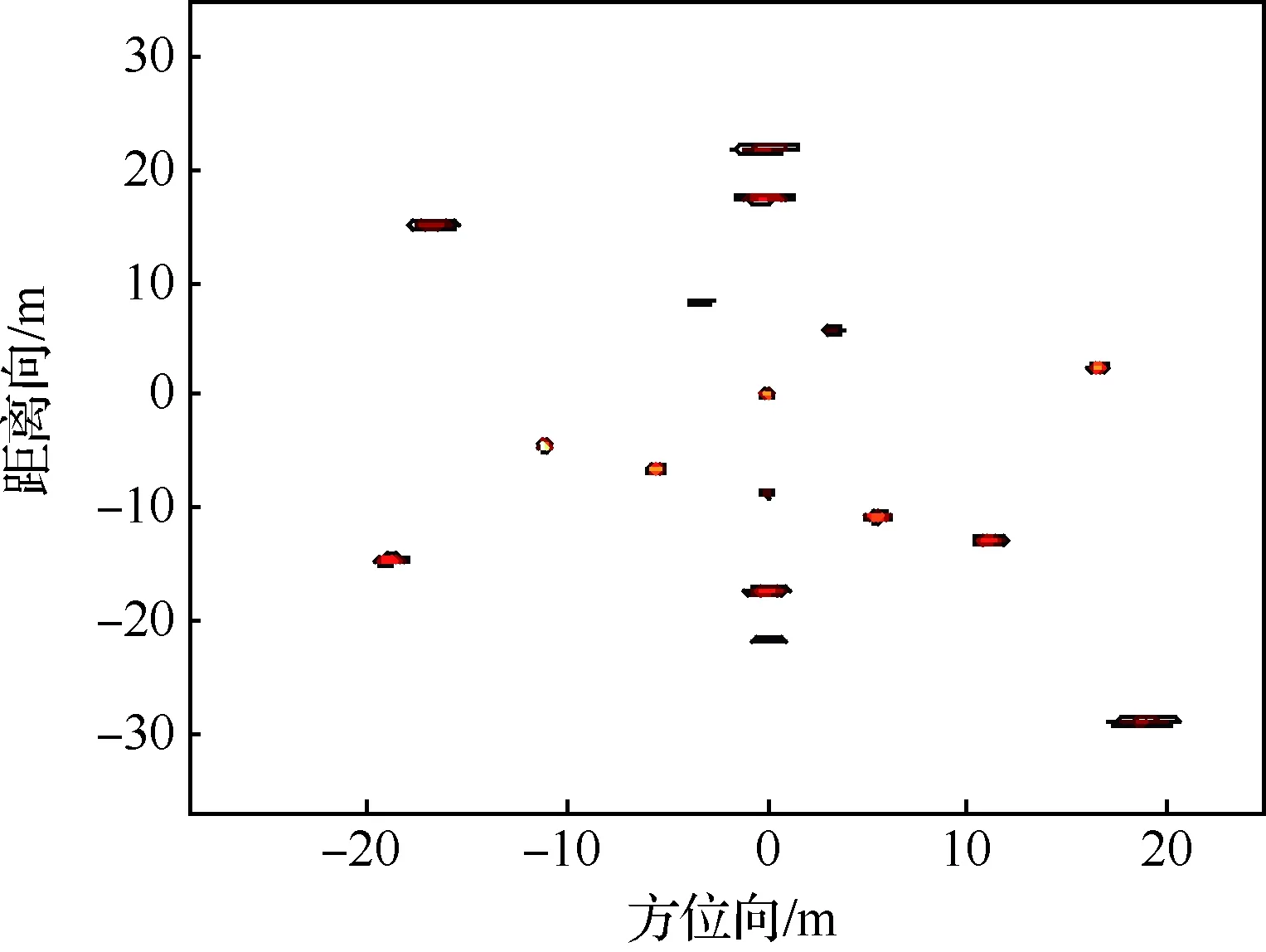
图10 越距离单元徙动校正后ISAR图像Fig.10 ISAR image after migration through range cell correction

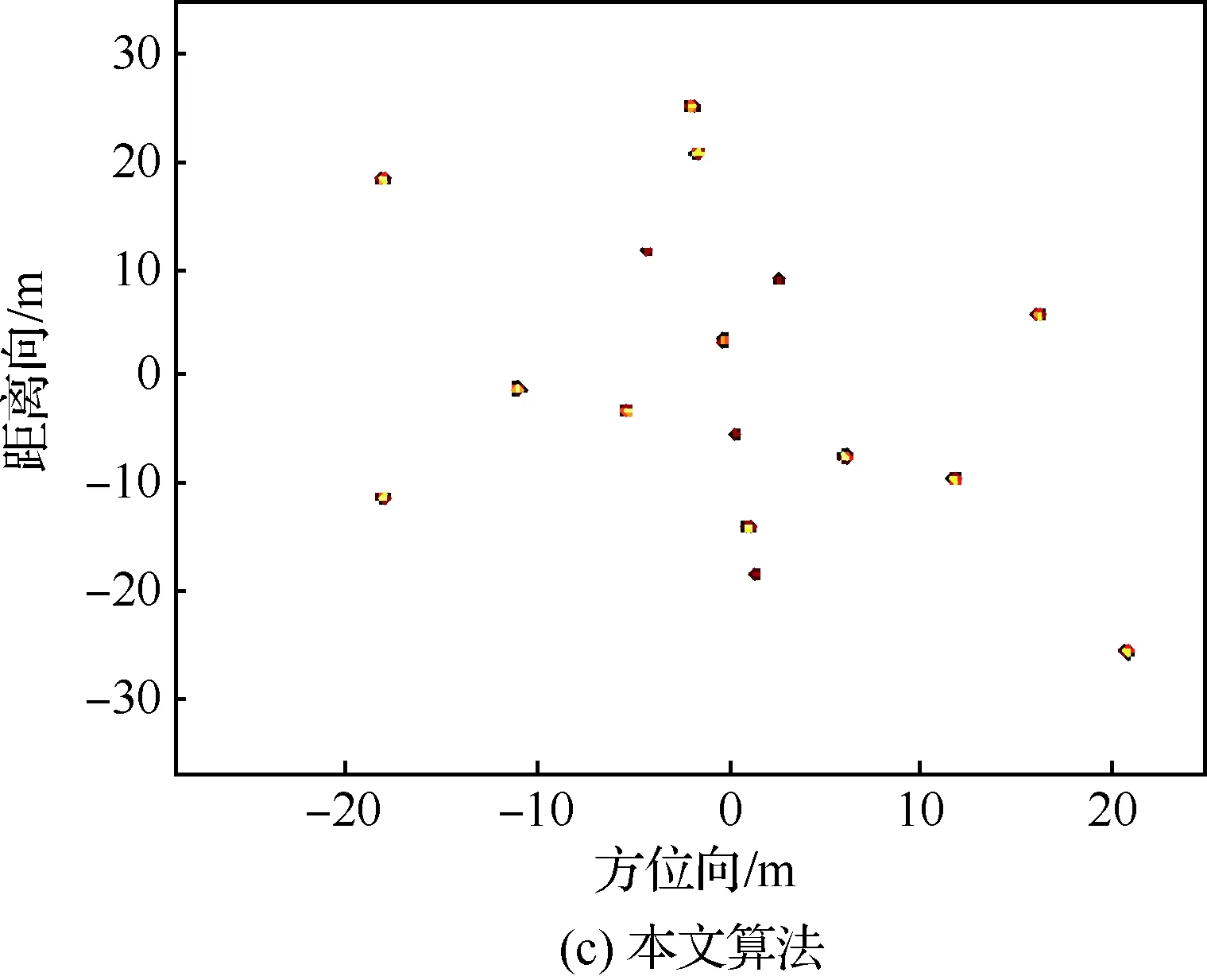
图11 越分辨单元徙动校正后的ISAR图像Fig.11 ISAR images after migration through resolution cell correction

此外，为定量分析成像质量，计算3幅图像的图像对比度，并统计图像上所有散射点的距离向和方位向3 dB主瓣平均宽度，如表3所示，数据对比表明了本文等效旋转中心估计算法的准确性。

表3 图像质量定量分析Table 3 Quantitative analysis of image quality

双基地ISAR的图像畸变校正利于后续的目标识别，根据图像畸变角度，可通过不同距离单元的移位操作实现图像的畸变校正，畸变校正后的结果如图12所示，其中图12(a)是RD直接成像结果(图9)校正后的图像，图12(b)是图11(a)图像畸变校正后的结果，图12(c)是图11(b)图像畸变校正后的结果，图12(d)是图11(c)图像畸变校正后的结果，可以看出畸变校正后的图像与仿真模型具有一致性(可通过定量计算散射点之间的夹角确定)，只存在视角的差异。

此外，为验证算法运算量，表4给出了算法及关键步骤运算时间统计，其中，距离单元搜索范围分别设置为400个和800个。仿真使用MATLAB软件，电脑配置为Win7操作系统、i7-4510 CPU、2.6 GHz主频、8 G内存。从表4可以看出，图像畸变校正过程所用时间最长，这是由于移位操作所用运算量较大，其次，图像旋转需要较大运算量。对比表中上下两组数据，当搜索距离单元个数不同时，算法运算总时间差异较大，若要进一步减小算法运算量，可通过减小距离单元搜索范围实现。

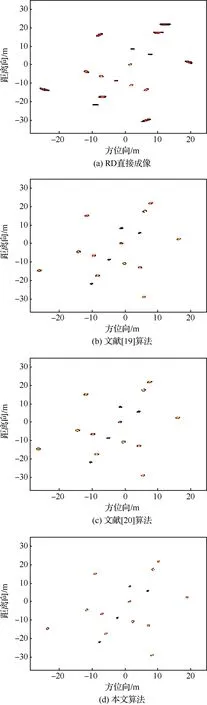
图12 畸变校正后的ISAR图像Fig.12 ISAR images after distortion correction

表4 运算时间统计Table 4 Statistics of calculation time

6 结 论

本文针对双基地角时变下的ISAR等效旋转中心估计问题，提出了一种等效旋转中心估计算法。主要结论如下：

1) 深入分析了双基地ISAR成像特性，并推导了图像畸变角度的表达式。

2) 算法考虑了双基地角时变引起的图像畸变，适用于双基地ISAR的等效旋转中心估计，应用范畴广。

3) 算法通过图像整体旋转估计目标的等效旋转中心，最大限度的利用了回波信息，等效旋转中心估计精度高。