考虑两种失效竞争的多状态冷贮备系统可靠性模型

陈童，谢经伟，狄鹏，尹东亮

海军工程大学 管理工程与装备经济系，武汉 430033

在航空航天、舰船以及核电等高风险领域，通常会采取冗余结构[1-3]以保证系统可靠性，例如动力系统中的备用泵组和电力系统中的备用配电板等。这些设备往往会由于磨损、疲劳、腐蚀等因素出现性能的不断退化，直至系统退化失效；此外，温度、电压、压力、振动等外部环境因素带来的冲击也可能导致系统突发失效。由于这2类失效的存在使得系统表现出多状态的特性，若简单的在可靠性建模过程中将系统状态分为工作与故障2类，显然难以满足对系统可靠性计算、评估等工作的实际需求，因此多状态系统可靠性理论[4-5]自20世纪80年代提出以来，已经成为了可靠性领域的主要研究方向之一。

显然，设备在使用过程中不仅会受性能退化的影响，同时也会受到外部冲击的影响，设备的失效是退化失效与突发失效相互竞争的结果[6]。An和Sun[7]认为高可靠性产品具有抵抗小型冲击的能力，假设在一定阈值内冲击会使得性能退化，当超过某一阈值时系统故障，在此基础上建立了微型发动机的可靠性模型；Yuan等[8]分别考虑退化过程与冲击过程独立与相关2种情况，对概率失效阈值不确定下的k/n系统进行了研究；王浩伟等[9]假设冲击流为Gamma过程，故障时间则采用Weibull分布进行描述，建立了竞争失效模式下的导弹可靠性模型；Levitinab和Finkelsteincd[10]则基于竞争失效理论对不可修并联系统可靠性问题进行了研究。

除了设计冗余结构提升系统可靠性外，往往还会通过维修活动来保证系统可靠性。常见的维修活动包括预防性维修与修复性维修。而在竞争失效系统中，退化与冲击可能对系统的不同部位造成不同程度的损伤，所以在对系统进行维修时，针对不同类型的损伤或者故障，往往需要不同的维修人员或维修工具进行修理，因此其维修时间分布也不尽相同。Riascos-Ochoa等[11]针对单部件竞争失效系统，根据部件的内部性能水平与外部冲击损伤等级设计了3种预防性维修方式，当故障时则进行换件维修；陈童和尹东亮[12-13]考虑维修优先权，采用保养与维修2种方式，分别对多状态冷贮备与多状态温贮备系统进行了研究。

针对竞争失效系统，许多研究采用定时维修策略与计划维修策略[14-15]，但往往可能会造成维修不及时或过度维修。而在航空航天、舰船等领域，大量的隐蔽性故障需要通过检测手段才能发现，而基于状态的维修恰恰能够通过检测手段探查系统状态，使得维修人员可视情采用不同的维修方式。通过这种维修策略，可有效保证系统可靠性水平并降低维修成本[16-17]。文献[17]采用年龄更换与定期检测策略，获得了竞争失效下单部件系统的最佳预防性维修间隔、检测间隔以及检测次数；Zhang等[18]采用双Wiener过程描述退化过程，外部冲击则采用齐次Poisson过程进行描述，对定期检测下的三态机械系统预防性维修策略进行了研究；Yue和Gao[19]则分别采用定期检测与随机检测策略，对退化系统进行了研究。

以往的这些研究通常考虑故障时间、维修时间等服从一些典型分布，如指数分布、Weibull分布、Erlang分布等，这样虽然能够降低模型的解析难度，但是却使得模型仅能够适用于一些特定情况，适用性受到很大限制。而Neuts和Meier[20]提出的PHase-type(PH)分布不仅保留了指数分布易于解析的特性，还能够拟合正数轴上任意分布，因此在复杂系统可靠性建模中能够描述各类复杂的随机分布，显示出良好的应用前景。例如，Kima和Kimb[21]采用PH分布描述不可修部件的工作时间，建立了冗余系统可靠性模型；王威等[22]研究了具有修理工多重休假的多部件系统，假设系统部件寿命、维修时间以及修理工休假时间均服从连续PH分布，得到了一系列可靠性指标；Ruiz-Oastro[23]假设冲击到达过程为离散PH更新过程，研究得到了累积冲击下的系统可靠性参数；Montoro和Pérezo[24]假设故障时间、检测时间以及维修时间均服从PH分布，研究了包含n个相同部件的温贮备系统，并分析了不同预防性维修阈值对系统可靠性指标的影响。

综上，本文以包含多个相同部件的冷贮备系统为研究对象，考虑随机检测策略，假设系统的3个不同类型的维修台能够根据系统状态分别提供预防性维修、退化失效的修复性维修以及突发失效的修复性维修服务，工作部件在各性能水平停留时间、各类维修时间等随机时间变量均采用PH分布进行描述，而外部的冲击到达过程则采用PH更新过程进行描述，建立了多状态冷贮备系统可靠性模型，得到了系统可靠性主要参数的解析表达式，并通过算例验证了模型的适用性，演示了3类维修速率及预防性维修阈值对系统可靠性指标的影响。

1 问题描述与假设

某冷贮备系统包含1个工作部件和k-1个相同的冷贮备部件，在时间t=0时，所有部件均完好。系统采用随机检测策略，维修台根据工作部件状态提供不同类型的维修服务：

1) 当部件性能退化到一定程度时进行预防性维修。

2) 当部件由于性能严重退化导致失效时进行退化失效修复性维修，称为Ⅰ类修复性维修。

3) 当部件由于致命突发冲击导致失效时进行突发失效修复性维修，称为Ⅱ类修复性维修。

针对不同类型维修需求，系统中有3个不同类型的维修台，分别提供预防性维修、Ⅰ类修复性维修与Ⅱ类修复性维修服务。

下面对该问题做进一步假设：

1) 令i表示工作部件所处性能水平，其中i∈{1,…,m1,m1+1,…,m2,m2+1}，m1和m2表示工作部件性能水平，将部件的性能水平划分为完好、一般和故障3类，其中1≤i≤m1时，部件性能处于完好状态；当m1+1≤i≤m2时，部件性能处于一般状态，即部件可以正常运行，但是性能较差；当i=m2+1时，部件处于故障失效状态，该部件需要用冷贮备部件替换下来。

2) 工作部件在各性能水平的停留时间具有fi阶PH表示(αi,Ti),αi为连续时间马尔科夫链的初始概率；Ti为瞬间状态之间的转移矩阵。

令piy(1≤i,y≤m2+1)表示部件性能从水平i下降到y的概率。

3) 当检测到工作部件性能水平位于一般状态时，工作部件需要接受预防性维修，其中检测时间分布具有ε阶PH表示(η,G)，预防性维修时间分布具有z1阶PH表示(β1,S1)。

4) 当工作部件性能退化直至故障时，则进入Ⅰ类修复性维修台，Ⅰ类修复性维修时间分布具有z2阶PH表示(β2,S2)。

5) 当发生致命的外部冲击时，工作部件即刻进入故障状态，该部件进入Ⅱ类修复性维修台，外部致命冲击的到达服从PH更新过程，具有t阶PH表示(γ,L)；Ⅱ类修复性维修时间分布具有z3阶PH表示(β3,S3)。

6) Ⅰ类修复性维修与Ⅱ类修复性维修具有优先权。当3个维修台分别对系统内部的k-1个部件进行维修时，若工作部件退化失效或突发失效，预防性维修台内正在进行维修的部件即刻转入工作状态，预防性维修台继续对下一个部件进行预防性维修，直至所有部件均进入Ⅰ类修复性维修台与Ⅱ类修复性维修台。

7) 当正进行预防性维修的部件中止维修进入工作状态时，部件返回至预防性维修阈值对应的性能水平m1。

在此基础上建立了如图1所示的2种失效竞争下多状态冷贮备系统可靠性模型。

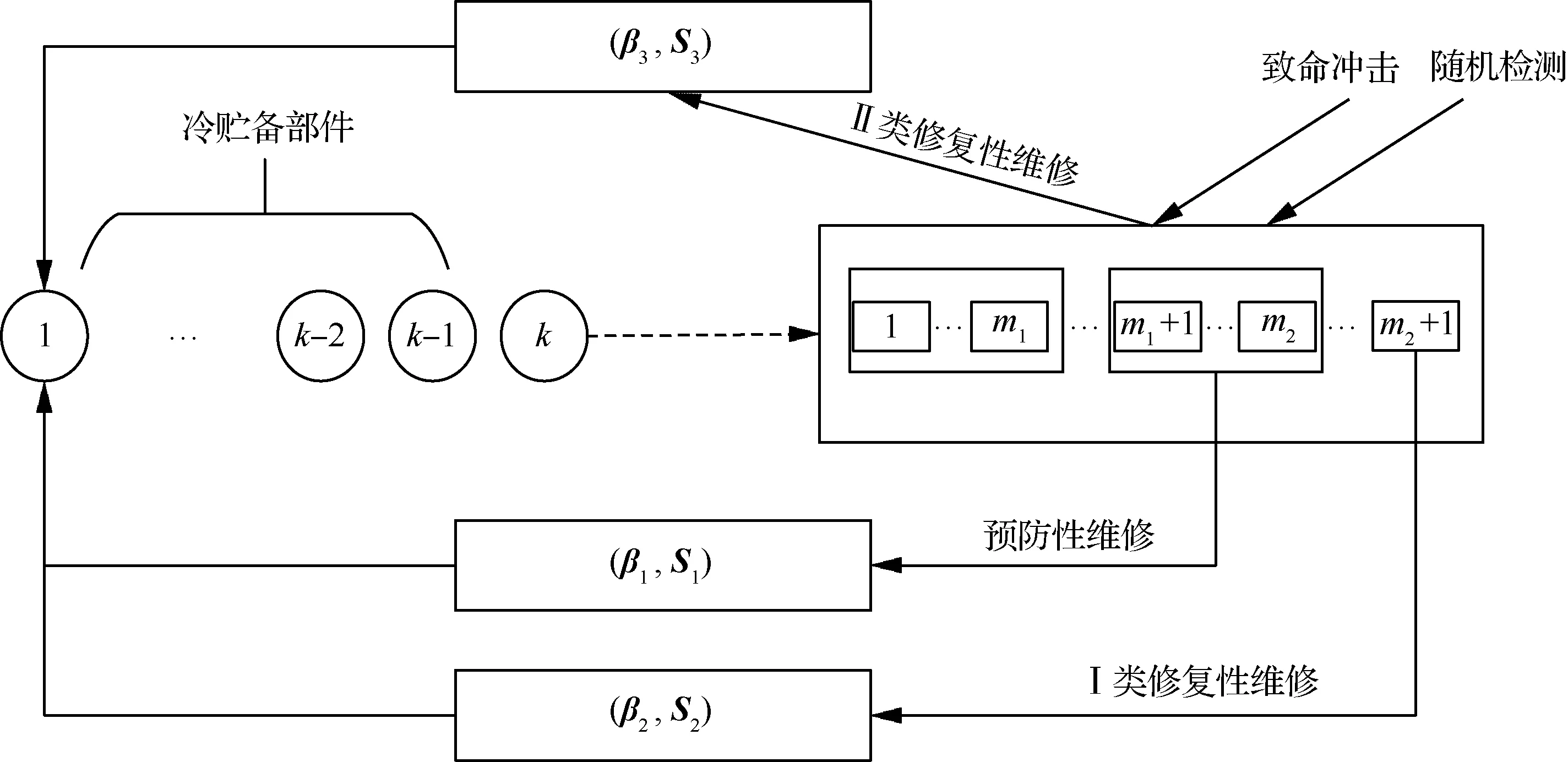
图1 模型示意图Fig.1 Diagram for model

2 模型构建

2.1 系统状态空间

假设在时刻t，工作部件性能处于水平i的x相位，检测和冲击的相位分别为h、l，维修台进行预防性维修、Ⅰ类修复性维修、Ⅱ类修复性维修的相位分别表示为r1、r2、r3；预防性维修台内正在维修的部件与待维修部件数量之和为l1,l1=0,1,…,k-1；Ⅰ类修复性维修台内正在维修的部件与待维修部件数量之和为l2,l2=0,1,…,k；Ⅱ类修复性维修台内正在维修的部件与待维修部件数量之和为l3,l3=0,1,…,k；M表示所有维修台内正在维修的部件与待维修部件数量之和(M=0,1,…,k)。考虑到3个维修台分别提供不同类型的维修活动，可将M表示为

当M=0,1,…,k-1时，有

M={(l1,l2,l3):0≤l1,l2,l3≤k-1,l1+l2+l3=M}

当M=k时，有

k={(0,l2,l3):l2+l3=k}

根据M可将系统的状态空间表示为Ω={M,M=0,1,…,k}

M=M1∪M2∪M3∪M4∪M5∪M6∪M7

M1={(M,0,0)},M2={(l1,l2,0)}，

M3={(0,M,0)},M4={(0,l2,l3)}，

M5={(0,0,M)},M6={(l1,0,l3)}，

M7={(l1,l2,l3)}。

具体含义为

1) 3个维修台均处于空闲状态，此时无部件需维修，系统正常运行：(0,0,0)={i,x,h,l}，其中1≤i≤m2,1≤x≤fi,1≤h≤ε,1≤l≤t。

2) 仅预防性维修台处于工作状态，此时预防性维修台内最多有k-1个部件，系统正常运行：(l1,0,0)={i,x,h,l,r1}，其中1≤i≤m2,1≤x≤fi,1≤h≤ε,1≤l≤t,1≤r1≤z1。

3) 仅Ⅰ类修复性维修台处于工作状态，若Ⅰ类修复性维修台内部件数量l2≤k-1，此时系统正常运行：(0,l2,0)={i,x,h,l,r2}，其中1≤i≤m2,1≤x≤fi,1≤h≤ε,1≤l≤t,1≤r2≤z2；若所有部件均处于Ⅰ类修复性维修台，此时系统故障：(0,k,0)={r2}，其中1≤r2≤z2。

4) 仅Ⅱ类修复性维修台处于工作状态，若Ⅱ类修复性维修台内部件数量l3≤k-1，此时系统正常运行：(0,0,l3)={i,x,h,l,r3},其中1≤i≤m2,1≤x≤fi,1≤h≤ε,1≤l≤t,1≤r3≤z3；若所有部件均处于Ⅱ类修复性维修台，此时系统故障：(0,0,k)={r3}，1≤r3≤z3。

5) 仅预防性维修台处于空闲状态，若Ⅰ类修复性维修台与Ⅱ类修复性维修台内部件数量l2+l3≤k-1，此时系统正常运行：(0,l2,l3)={i,x,h,l,r2,r3}，其中1≤i≤m2,1≤x≤fi,1≤h≤ε,1≤l≤t,1≤r2≤z2,1≤r3≤z3,l2=1,2,…,k-2,l3=M-l2；若所有部件均故障，此时系统故障：(0,l2,l3)={i,x,h,l,r2,r3}，其中1≤i≤m2,1≤x≤fi,1≤h≤ε,1≤l≤t,1≤r2≤z2,1≤r3≤z3,l2=1,2,…,k-1,l3=k-l2。

6) 仅Ⅰ类修复性维修台处于空闲状态，由于Ⅱ类修复性维修较预防性维修具有优先权，当预防性维修台工作时，至少有一工作部件，此时系统运行：(l1,0,l3)={i,x,h,l,r1,r3}，其中1≤i≤m2,1≤x≤fi,1≤h≤ε,1≤l≤t,1≤r1≤z1,1≤r3≤z3,l1=1,2,…,k-2,l3=M-l1。

7) 仅Ⅱ类修复性维修台处于空闲状态，由于Ⅰ类修复性维修较预防性维修具有优先权，当预防性维修台工作时，至少有一工作部件，此时系统运行：(l1,l2,0)={i,x,h,l,r1,r2}，其中1≤i≤m2,1≤x≤fi,1≤h≤ε,1≤l≤t,1≤r1≤z1,1≤r2≤z2,l1=1,2,…,k-2,l2=M-l1。

8) 3个维修台均处于工作状态，由于Ⅰ类修复性维修与Ⅱ类修复性维修较预防性维修具有优先权，当预防性维修台工作时，至少有一工作部件，此时系统运行：(l1,l2,l3)={i,x,h,l,r1,r2,r3}，其中:1≤i≤m2,1≤x≤fi,1≤h≤ε,1≤l≤t,1≤r1≤z1,1≤r2≤z2,1≤r3≤z3,l1=1,2,…,k-3,l2=1,2,…,k-3,l3=M-l1-l2。

2.2 无穷小生成元

根据系统状态空间的划分，可得系统在整个状态空间的转移速率矩阵，即该马尔科夫链的无穷小生成元Q。

Q=

式中:B00表示系统在状态空间M=0的内部转移;B01、B10、C(1)、C(2)、D(1)、D(2)、E(2)、B(k-1)(k-1)、B(k-1)k、Bk(k-1)、Bkk均表示状态之间的转移矩阵。

系统各状态之间的转移关系如图2所示。

当检测到工作部件性能水平时，性能水平通过矩阵U1、U2引入。

图2 系统状态转移示意图Fig.2 Diagram for system state transition

为表述方便，令

1) 状态空间M=0的内部转移

B00表示系统在状态空间M=0的内部转移，T⊗Itε表示工作部件性能水平i之间转移，冲击与检测的相位未发生改变；Io⊗L⊗Iε表示冲击未发生，工作部件性能水平与检测相位未发生改变；U1⊗It⊗G0η表示检测设备检测到工作部件处于完好状态，冲击的相位未发生改变；Iot⊗G表示检测未发生，工作部件性能水平与冲击相位未发生改变。

B00=T⊗Itε+Io⊗L⊗Iε+U1⊗It⊗

G0η+Iot⊗G

2) 状态空间M=0与M=1之间的转移

① 检测到工作部件处于一般状态，该部件进入预防性维修台，冷贮备部件进入工作状态，转移速率矩阵为B01(1):

式中:en为元素为1的n×1列向量。

② 工作部件退化失效，该部件进入Ⅰ类修复性维修台，冷贮备部件进入工作状态，转移速率矩阵为B01(2):

③ 工作部件突发失效，该部件进入Ⅱ类修复性维修台，冷贮备部件进入工作状态，转移速率矩阵为B01(3):

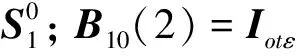
3) 状态空间M=1,2,…,k-2的内部转移

C(M)表示系统在状态空间M=1,2,…,k-2的内部转移，此时系统内无新的部件需要进入维修台进行维修。

C(M)=

M=3,4,…,k-2

C(2)=

G0η⊗Iz1+Iot⊗G⊗Iz1+Iotε⊗S1

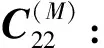
U1⊗It⊗G0η⊗Iz1z2+Iot⊗G⊗Iz1z2+

Iotε⊗S1⊗Iz2+Iotεz1⊗S2}

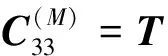
G0η⊗Iz2+Iot⊗G⊗Iz2+Iotε⊗S2

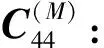
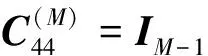
U1⊗It⊗G0η⊗Iz2z3+Iot⊗G⊗Iz2z3+

Iotε⊗S2⊗Iz3+Iotεz2⊗S3}

G0η⊗Iz3+Iot⊗G⊗Iz3+Iotε⊗S3

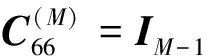
U1⊗It⊗G0η⊗Iz1z3+Iot⊗G⊗Iz1z3+

Iotε⊗S1⊗Iz3+Iotεz1⊗S3}

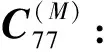
U1⊗It⊗G0η⊗Iz1z2z3+Iot⊗G⊗Iz1z2z3+

Iotε⊗S1⊗Iz2z3+Iotεz1⊗S2⊗Iz3+

Iotεz1z2⊗S3}

4) 状态空间M向M+1的转移(M=1,2,…,k-2)

D(M)表示系统从状态空间M转移到M+1，此时工作部件需要进入维修台进行维修活动，冷贮备部件进入工作状态。

① 检测到工作部件性能处于一般状态，该部件进入预防性维修台。

② 工作部件退化失效，该部件进入Ⅰ类修复性维修台。

③ 工作部件突发失效，该部件进入Ⅱ类修复性维修台。

D(M)=

M=3,4,…,k-2

D(2)=

D(1)=

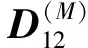
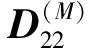
① 检测到工作部件性能处于一般状态，该部件转入预防性维修台，冷贮备部件进入工作状态，即(l1,l2,0)→(l1+1,l2,0)。

② 工作部件退化失效，该部件进入Ⅰ类修复性维修台，冷贮备部件进入工作状态，即(l1,l2,0)→(l1,l2+1,0)。

式中：

j=1,2,…,M-1

j=1,2,…,M-1

① 检测到工作部件处于一般状态，该部件进入预防性维修台，即(l1,l2,l3)→(l1+1,l2,l3)。

② 工作部件退化失效，该部件进入Ⅰ类修复性维修台，即(l1,l2,l3)→(l1,l2+1,l3)。

③ 工作部件突发失效，该部件进入Ⅱ类修复性维修台，即(l1,l2,l3)→(l1,l2,l3+1)。

式中：

j=1,2,…,M-2

j=1,2,…,M-2

j=1,2,…,M-2

同理可知：

[00[U2eoα1⊗It⊗G0η⊗β3⊗Iz2z30]]

式中：

j=1,2,…,M-1

j=1,2,…,M-1

式中：

j=1,2,…,M-1

j=1,2,…,M-1

5) 状态空间M向M-1的转移(M=2,3,…,k-1)

E(M)表示系统从状态空间M转移到M-1,M=2,3,…,k-1，此时维修台内减少1个待修部件。

① 预防性维修台内减少1个待修部件，即(l1,l2,l3)→(l1-1,l2,l3)。

② Ⅰ类修复性维修台内减少1个待修部件，即(l1,l2,l3)→(l1,l2-1,l3)。

③ Ⅱ类修复性维修台内减少1个待修部件，即(l1,l2,l3)→(l1,l2,l3-1)。

E(M)=

M=4,5,…,k-1

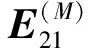
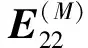
① 预防性维修台内减少一个待修部件，即(l1,l2,0)→(l1-1,l2,0)。

② Ⅰ类修复性维修台内减少一个待修部件，即(l1,l2,0)→(l1,l2-1,0)。

式中：

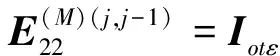
j=2,3,…,M-1

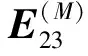
① 预防性维修台内减少1个待修部件，即(l1,l2,l3)→(l1-1,l2,l3)。

② Ⅰ类修复性维修台内减少1个待修部件，即(l1,l2,l3)→(l1,l2-1,l3)。

③ Ⅱ类修复性维修台内减少1个待修部件，即(l1,l2,l3)→(l1,l2,l3-1)。

式中：

j=1,2,…,M-3

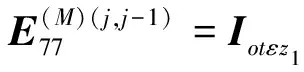
j=2,3,…,M-2

j=3,4,…,M-1

同理可知：

式中：

其中：

6) 状态空间M=k-1的内部转移

B(k-1)(k-1)表示系统在状态空间M=k-1的内部转移，由于两类修复性维修具有较高的优先等级，因此转移速率矩阵B(k-1)(k-1)内包含了预防性维修台向其他维修台的转移。

B(k-1)(k-1)=

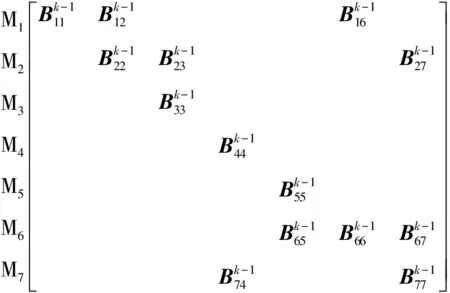
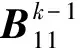
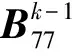
① 3个维修台均处于工作状态，工作部件未进入故障状态。

② 3个维修台均处于工作状态，工作部件退化失效，正在进行预防性维修的部件停止维修进入工作状态，待修部件进入预防性维修台。

③ 3个维修台均处于工作状态，工作部件突发失效，正在进行预防性维修的部件停止维修进入工作状态，待修部件进入预防性维修台。

式中：

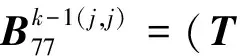
j=1,2,…,k-3

j=2,3,…,k-3

j=3,4,…,k-3

同理可知：

[[eoαm1⊗L0γ⊗Iε⊗ez1β1⊗β30]0]

[0[eoαm1⊗L0γ⊗Iε⊗ez1β1⊗Iz2⊗β30]]

[0[T0αm1⊗Itε⊗ez1β1⊗β2⊗Iz30]]

式中：

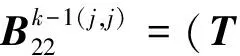
j=1,2,…,k-2

j=2,3,…,k-2

其中：

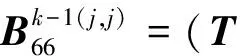
j=1,2,…,k-2

j=2,3,…,k-2。

7) 状态空间M=k-1与M=k之间的转移

B(k-1)k表示系统从状态空间M=k-1转移到状态空间M=k，Ⅰ类修复性维修台与Ⅱ类修复性维修台对k-1个故障部件进行修复性维修，此时工作部件退化失效或突发失效，系统完全故障。

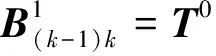
式中：

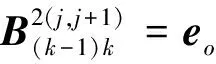
Bk(k-1)表示系统从状态空间M=k转移到状态空间M=k-1，修复性维修台对其中一个故障部件修理完成，该部件进入工作状态，系统正常运行。

式中：

j=1,2,…,k-2

j=2,3,…,k-1

8) 状态空间M=k的内部转移

Bkk表示系统在状态空间M=k的内部转移，此时系统内部有k个故障部件，Ⅰ类修复性维修台与Ⅱ类修复性维修台对故障部件进行修理。

2.3 稳态概率向量

当系统进入稳态时，无穷小生成元中各个状态对应的概率组成了稳态概率向量π=(π0,π1,…,πM,…,πk-1,πk)，且满足以下方程：

(1)

式中:Q为连续时间马尔科夫链无穷小生成元。

将式(1)展开可得

π0B00+π1B10=0

(2)

π0B01+π1C(1)+π2E(2)=0

(3)

πj-1C(j-1)+πjD(j)+πj+1E(j+1)=0

j=2,3,…,k-2

(4)

πk-1B(k-1)k+πkBkk=0

(5)

解上述方程组式(1)，可得到各状态空间对应的稳态概率向量。

3 系统可靠性指标

3.1 系统稳态可用度

系统稳态可用度表示系统经过长期运行，处于运行状态的概率。即系统处于状态空间Ω*={M,M=0,1,…,k-1}的概率，可得系统稳态可用度A。

(6)

3.2 系统可靠度函数

系统可靠度函数表示系统在时刻t之前不发生故障的概率。对于本文模型，系统可靠度是指系统在时刻t之前处于状态空间Ω*={M,M=0,1,…,k-1}的概率，将系统故障状态M=k合并为吸收状态，对应的状态转移矩阵Q*为

状态转移矩阵Q*表示系统不处于故障状态时，系统在其余状态空间之间的转移情况。令Wi(t)表示系统处于状态空间Ω*={M,M=0,1,…,k-1}的概率向量；且Wi(t)、Q*满足下列微分方程：

(7)

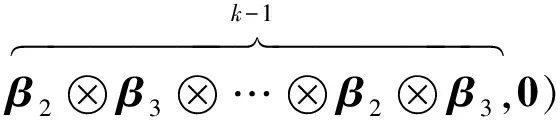
解微分方程组，可得系统可靠度函数R(t)。

R(t)=φexp(Q*t)e

(8)

3.3 系统平均故障间隔时间

系统平均故障间隔时间是指系统从故障状态离开又重新回到故障状态的间隔时间。当系统离开故障状态M=k时，系统正常运行，当系统重新进入状态M=k时，系统故障。由PH分布定义可知，系统平均故障间隔时间服从PH分布，有otε[(1+(k-1)(z1+z2+z3)+(k-2)(z1z2+z1z3+z2z3)+(k-3)z1z2z3)]阶不可约表示(φ,Q*)。

MTBF=-φQ*-1e

(9)

3.4 系统故障率

系统故障率是指系统在单位时间内进入故障状态的次数，记为r，根据系统状态转移矩阵Q有

r=πk-1B(k-1)ke

(10)

4 算 例

4.1 模型适用性验证与预防性维修阈值变化对系统可靠性指标影响

1)模型适用性验证

已知某冷贮备系统由5个相同部件组成，工作部件共存在7个性能水平，假设m1=1，即将性能水平{1}划分为完好状态，{2,3,4,5,6}归为一般状态，{7}为系统退化失效状态。

对该系统长期的运行与维修记录数据进行分析，利用文献[25]中方法将可靠性数据以及其他分布拟合为PH分布形式，可得工作部件在各性能水平的停留时间分布，如表1所示。

表1工作部件在各性能水平停留时间分布

Table1Residencetimesindifferentperformancelevelsoftheoperationalunit

i停留时间分布1α1=[0.1990.2270.574]T1=-0.1470.0160.0174.976-10.3281.8720.1360.048-0.946éëêêùûúú2α2=[010]T2=-5.753000-5.7535.7535.7530-5.753éëêêùûúú3α3=[0.6560.30.044]T3=-1.2341.0110.1790-1.2341.23400-1.234éëêêùûúú4α4=[010]T4=-5.999000-5.9995.9995.9990-5.999éëêêùûúú5α5=[0.0230.9590.018]T5=-4.37400.0152.574-4.3881.7580.0920-4.392éëêêùûúú6α6=[100]T6=-6.430.4300.65-5.7400.0920-4.392éëêêùûúú

该马尔科夫链的无穷小生成元Q为

将数据代入模型，计算可得稳态可用度A=0.944 0，故障率r=0.019 8次/单位时间，平均故障间隔时间MTBF=52.708 7单位时间，系统可靠度函数如图3所示。

该算例说明当部件在各性能水平的停留时间、检测时间、维修时间等服从不同类型的分布时，将其拟合为PH分布形式进行可靠性解析建模，能够有效降低模型的解析难度，模型的适用性显著提升。

2) 预防性维修阈值对系统可靠性指标的影响

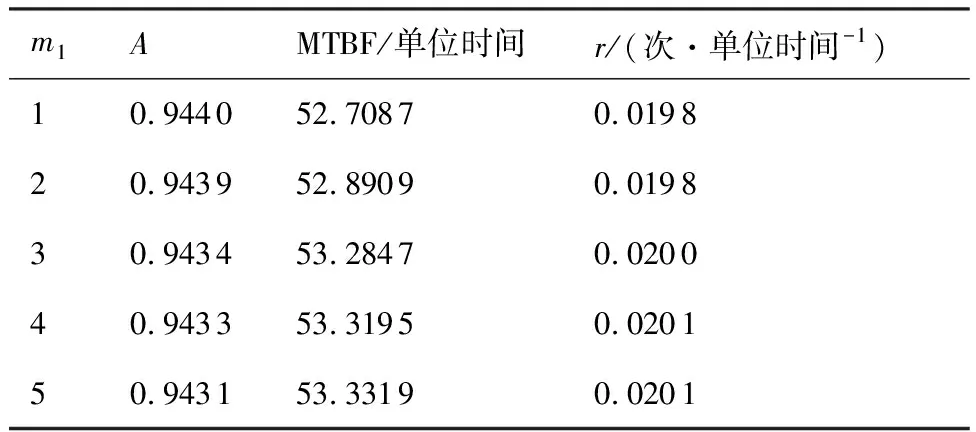
当改变预防性维修阈值时，系统可靠性指标变化如表2所示。

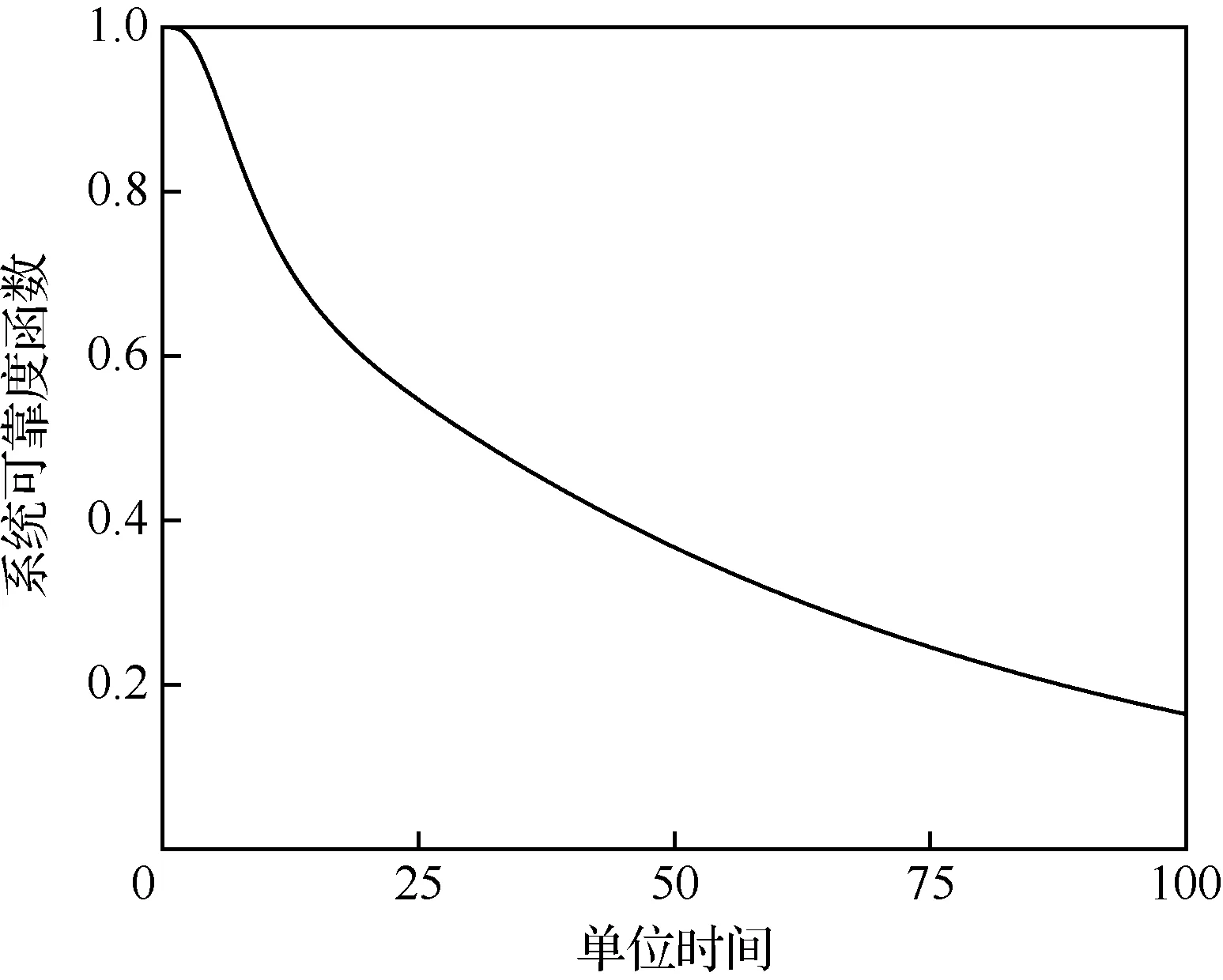
图3 时间与可靠度关系Fig.3 Variation of system reliability with time

表2预防性维修阈值对系统可靠性指标的影响

Table2Variationofpreventivemaintenancethresholdwithsystemreliabilityindex

m1AMTBF/单位时间r/(次·单位时间-1)10.944052.70870.019820.943952.89090.019830.943453.28470.020040.943353.31950.020150.943153.33190.0201

由表2可知，提高预防性维修阈值虽然能够提升系统平均故障间隔时间，延长部件的工作时间，但是系统的稳态可用度会随之降低，系统故障率也随之增加。

4.2 预防性维修台工作速率对系统可靠性影响

为直观展示预防性维修速率对系统可靠性指标的影响，在m1=1时，令β1=1,S1=(-λ)，改变指数分布参数。计算结果如图4～图6所示。

由图4～图6可知，在本算例中，随着预防性维修速率的增加，系统稳态可用度呈现出先增后减的趋势，系统故障率呈现出先减后增的趋势，而系统平均故障间隔时间则随着预防性维修速率的增加而增加并趋于平稳。这是因为预防性维修速率的改变不仅影响着系统工作时间与预防性维修时间，还会在一定程度上影响修复性维修时间以及系统故障频度，在修复性维修速率一定的情况下，随着预防性维修速率的增加，系统在工作状态的时间较修复性维修时间变化较快，而后较慢，这就导致了系统稳态可用度与系统故障频率呈现出由图4～图5的趋势，与此同时，预防性维修改变了工作部件处于完好状态与一般状态的停留时间，故系统平均故障间隔时间呈现出图6的趋势。

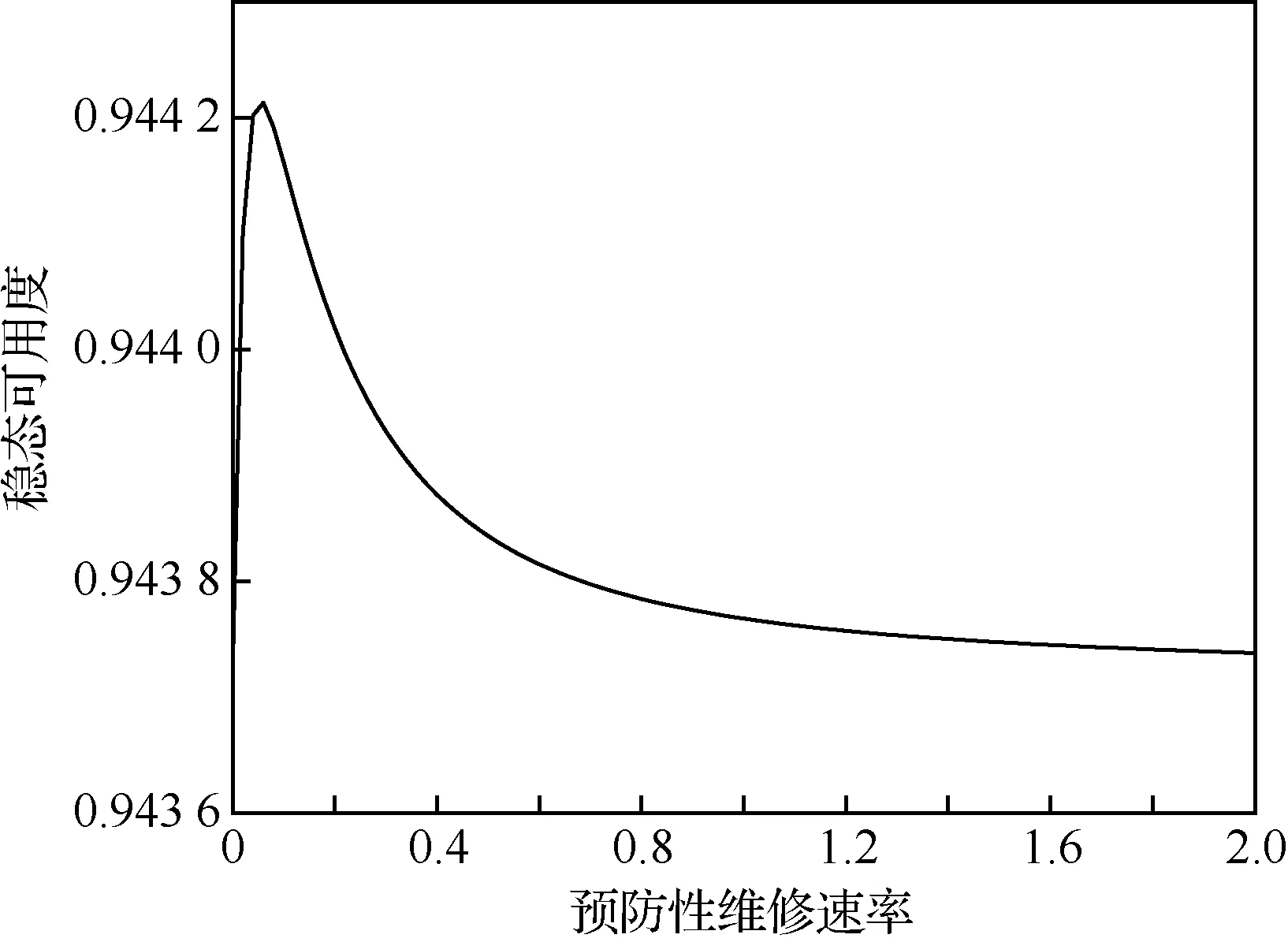
图4 预防性维修速率对稳态可用度的影响Fig.4 Effect of preventive maintenance rate on system stationary availability

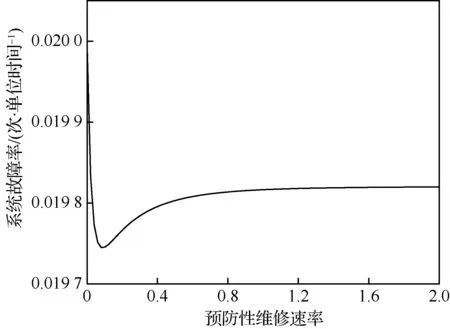
图5 预防性维修速率对系统故障率的影响Fig.5 Effect of preventive maintenance rate on system failure rate

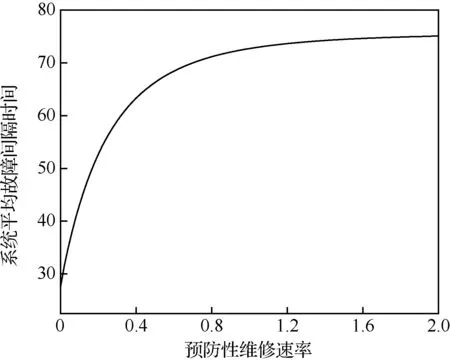
图6 预防性维修速率对系统平均故障间隔时间的影响Fig.6 Effect of preventive maintenance rate on mean time between system failure

4.3 两类修复性维修速率对系统可靠性影响

同样，令S2=(-μ),S3=(-ρ)，研究2类修复性维修速率同时变化对系统可靠性指标的影响。计算所得结果如图7～图9所示。

图7～图9可知，在一定的Ⅰ类修复性维修速率下，Ⅱ类修复性维修速率改变的同时，系统处于工作状态的时间与Ⅰ类修复性维修的时间也在改变，因此系统稳态可用度会呈现出先增后减或一直增加趋于平稳的态势；当两类修复性维修速率改变，系统稳态概率向量πk-1与转移速率矩阵B(k-1)k的变化程度不一，因此系统故障率会呈现出先增后减的趋势；而修复性维修能够直接影响系统的工作时间，因此系统平均故障间隔时间与修复性维修几乎呈现出线性关系。

图7 两类修复性维修速率对稳态可用度的影响Fig.7 Effect of corrective maintenance rate on system stationary availability

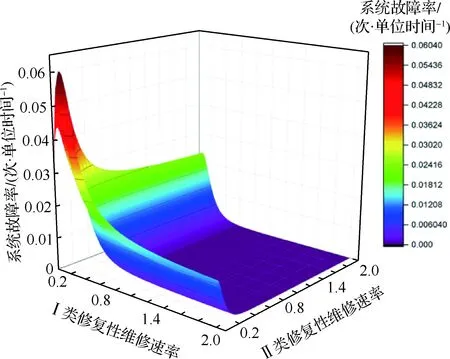
图8 两类修复性维修速率对系统故障率的影响Fig.8 Effect of corrective maintenance rate on system failure rate

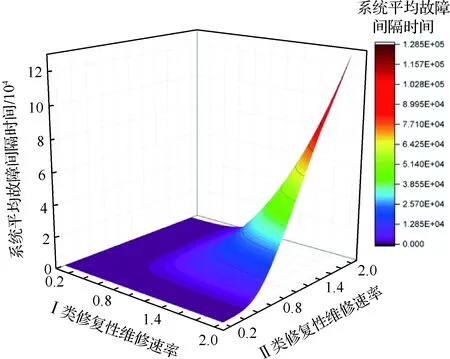
图9 两类修复性维修速率对系统平均故障间隔时间的影响Fig.9 Effect of corrective maintenance rate on mean time between system failure

由上述结果分析可知，随着维修速率的增加，系统可靠性指标能够得到一定程度的提升，而当维修速率增加到一定程度时，其对系统可靠性指标的影响程度会减少。因此，可以通过合理选择预防性维修阈值、预防性维修与修复性维修的维修速率，在有效保证可靠性的基础上，节约维修资源。

5 结 论

本文采用PH分布与PH更新过程研究了退化失效与突发失效竞争的多状态冷贮备系统可靠性规律。通过数值算例分析了预防性维修阈值以及3类维修速率对系统可靠性指标的影响，结论如下：

1) 预防性维修阈值增加会使得系统稳态可用度降低，而故障率与平均故障间隔时间会随之增加。

2) 通过分析3类维修速率变化对系统可靠性指标的影响，便于在保证系统可靠性的基础上，节约维修资源。

3) 采用PH分布等工具研究多状态复杂系统，能够在保证良好解析特性的同时大幅提升模型的适用性。