透视“隐圆”，让其“圆形”毕*

江苏省常州高级中学 (213003) 周 洁 杨元韡

求曲线的轨迹方程是解析几何研究的两大基本问题之一．但在有些解析几何问题中，看不到动点满足的轨迹的直接条件，读不出求动点轨迹重要性或必要性，而是将轨迹的条件极其隐晦地融入到条件中，求轨迹的重要性或必要性在解题过程中却体现得淋漓尽致．解决这类问题往往需要解题者自主探索并发现轨迹，并能灵活运用轨迹实现问题的转化．而圆作为一个极其完美的图形之一，其轨迹常常会用多种形式来隐晦地表达，我们把它称之为“隐圆”．利用“隐圆”的条件，常常来考察直线与圆、圆与圆的位置关系、线段的长或参数的最值等问题．

笔者对近些年含有“隐圆”条件的典型高考题和模拟题进行了较为系统梳理，并总结了几种常见的“隐圆”的“隐”的方式，有些还从不同的角度去解读，让其“圆形”毕露的同时，也提高学生对条件的转化能力．

1.平面内，到定点的距离等于定长(大于0)的点的轨迹为圆，这是圆的定义．直接利用圆的定义是设计“隐圆”条件的最基本的方式．

例1 如果圆(x-2a)2+(y-a-3)2=4上总存在两个点到原点的距离为1，求实数a的取值范围．

评析：注意到到原点距离为1的点的轨迹为以原点为圆心的单位圆x2+y2=1，则可将原条件转化成已知圆与“隐形”圆x2+y2=1相交．

例2 (2016年南京二模第12题)已知圆O:x2+y2=1，圆M:(x-a)2+(y-a+4)2=1，若圆M上存在点P，过点P作圆O的两条切线，切点为A,B，若∠APB=60°，则a的取值范围为．

评析：根据平面几何的知识得到OP=2，因此点P的轨迹是“隐圆”x2+y2=4．于是原条件可转化成“隐圆”x2+y2=4与圆M有公共点．

2．平面内，设A，B为定点且AB=a，若PA=λPB(λ为常数，λ>0且λ≠1)，则点P的轨迹为圆．

平面内到两定点的距离之比为常数λ(λ>0且λ≠1)的点的轨迹为圆，该圆称为阿波罗尼斯圆，证明过程略．利用阿波罗尼斯圆为背景设置“隐圆”条件，在江苏省近十年高考中出现两次，在各地模拟题中也经常出现．

评析：从解析几何角度，以AB所在的直线为x轴，AB的中点为坐标原点，建立直角坐标系xOy，很容易得出点C的轨迹为两段圆弧(注：实质上是圆去掉与直线AB的交点)，其方程为(x-3)2+y2=8(y≠0)．明显，边AB上高的最大值为圆的半径，从而易得三角形ABC的面积的最大值．

例4 (2013年江苏高考第17题)在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心C在直线l上.(1)略；(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.

评析：第(2)问点M在由MA=2MO确定的“隐圆”上，其方程为x2+(y+1)2=4.又点M在圆C上，进而原条件转化成“隐圆”与圆C有公共点．

图1

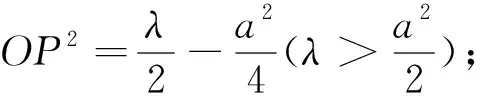
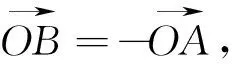
特别地，当λ=0时，点P的轨迹为以AB为直径的圆，这实质上与点P对线段AB的两个端点的张角为90°，或者直线PA、PB的斜率互为负倒数(在斜率都存在的条件下)都是两两等价的，这里就不再举例说明．

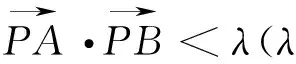
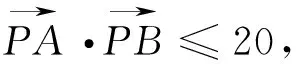
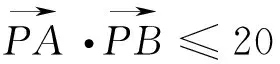
图2

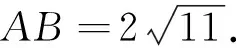
结语：文中对常见的“隐圆”的“隐”的方式进行了剖析，并举例说明．当然，“隐圆”的“隐”的方式也未必只有这几种，可能还有其他的方式．而“隐圆”的相关问题常常在知识的交汇处命题，因此学生必须对相关知识以及知识间的联系熟练掌握才能顺利求解这类问题．本文旨在揭示了动点满足某些形式的条件是可以得到动点的轨迹是圆(或圆内、圆外)，并尽可能给出多个角度的解读，强化学生利用动点的轨迹去研究与圆相关问题的意识，进一步培养学生的转化与化归能力．