2018年江苏卷13题的多角度探究
2019-02-18 03:00江西省南昌市第十五中学330039龙光鹏黄称文
中学数学研究(江西) 2019年1期
江西省南昌市第十五中学 (330039) 龙光鹏 黄称文
1.试题呈现
在ΔABC中,角A,B,C的对边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为.
本试题主要考察学生解三角形与用基本不等式求最值,即运用正弦定理和余弦定理求解边角的关系,利用基本不等式求解代数式的最值,注意等号成立的条件.考察内容丰富,综合性较强,本文拟从不同角度对此题作多角度的探究.
2.探究过程
根据试题的条件,分析条件之间的关系,首先探讨a,c边之间的关系,再探究4a+c的最小值,所以本试题可以分为两大问题进行探究.
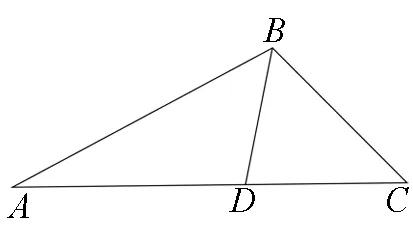
图1
解析:(面积法)∵SΔABC=SΔABD+SΔBCD,
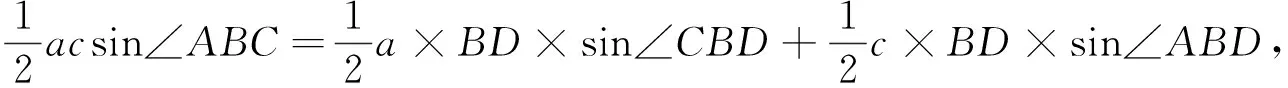

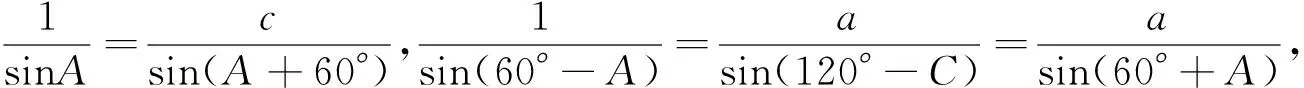
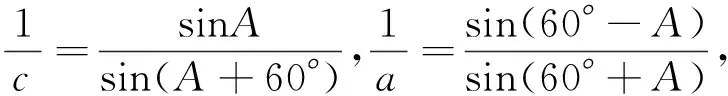
猜你喜欢
新高考·高三数学(2022年3期)2022-04-28
中学生数理化·七年级数学人教版(2021年9期)2021-11-20
中学生数理化·高一版(2021年4期)2021-07-19
新世纪智能(数学备考)(2021年11期)2021-03-08
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14
中学生数理化·七年级数学人教版(2020年9期)2020-11-16
中学生数理化(高中版.高二数学)(2020年10期)2020-11-10
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
中学生数理化·七年级数学人教版(2019年9期)2019-11-16
小学生作文(中高年级适用)(2018年5期)2018-06-11

