挖掘教材例题潜在功能 提高学习效率

安徽省无为中学 (238300) 丁福全

苏联数学教育家奥加涅相说过：“必须重视，很多习题潜在的进一步扩展其数学功能、发展功能与教育功能的可能性……”.中学数学教材中的例(习)题，凝聚了几代专家、学者的集体智慧与结晶，一般具有典型性、代表性、示范性与明确的针对性，因此研究这些例(习)题，挖掘隐藏其背后的数学思想、方法、定理不仅能够培养学生的探究能力，提高学习效率，而且还能在学生“最近发展区”产生认知冲突，从而构建新的知识体系，同时也能促进学生重视数学教材，不搞题海战术，减轻过重的学习负担.

本文以人教版高中数学教材中的例习题为例并结合相关的高考试题，说明在教学过程中如何挖掘教材例习题的潜在功能，让学生在学到数学知识、思想、方法的同时，更能体会到教材中的例习题是如何与高考试题发生联系的.

案例1 (人教版高中数学必修4第105页例2)对任意的a,b∈R恒有(a+b)2=a2+2ab+b2，

(a+b)(a-b)=a2-b2.

教材利用向量数量积的运算律对①式进行了证明.本例到此为止，学生只能通过本例掌握了向量数量积的乘法运算法则.若能引导学生运用类比方法对此例作如下探究：

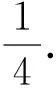
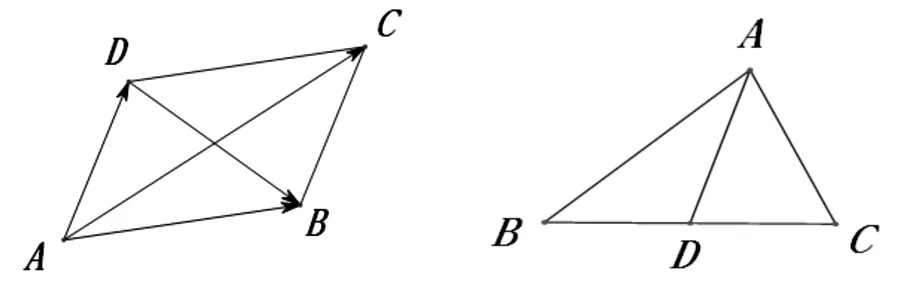
图1图2

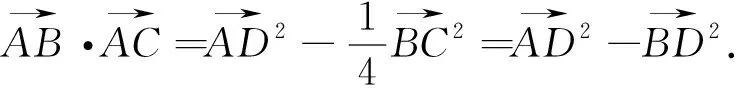
极化恒等式将平面向量的数量积运算转化为两个平面向量的长度运算，使不可度量的数量积关系转化为可度量、可计算的数量关系.极化恒等式的应用十分广泛，利用它可以快速有效地解决与向量的数量积有关的最值、范围、模长等问题.下面以两道高考试题说明.

图3

解：由极化恒等式可得

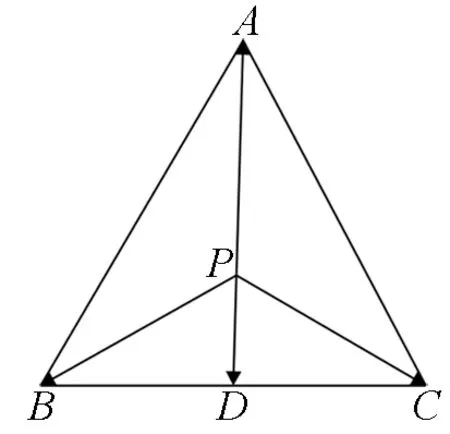
图4

南粤古驿道分布广泛，沿途自然条件和历史人文底蕴各不相同，南粤古驿道标识系统的建设效果对打造连续完整、具有整体效果的南粤古驿道历史游径具有重要意义。目前，南粤古驿道标识系统以《南粤古驿道标识系统设计指引》为基础，在乳源西京古道、南雄梅关古道等地进行了诸多尝试，标识主要类型集中于指引类和记名类，对于标识的特色化实践仍有待加强。美国历史游径标识系统从多个方面为南粤古驿道标识系统的设计和表现方式提供了参考和借鉴，南粤古驿道标识系统在吸取其经验的同时，更应当在功能和表现上融入古驿道深厚的历史文化内涵和独特的地域风情，形成富有特色的南粤古驿道标识系统，并以此为媒介，提升地方的知名度和乡村的活力。

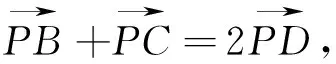
当且仅当点P为线段AD的中点时取等号.

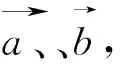
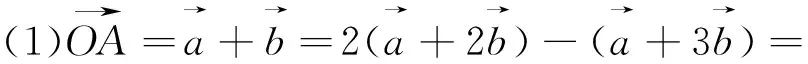
图5

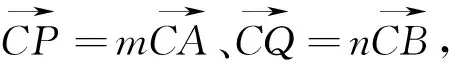
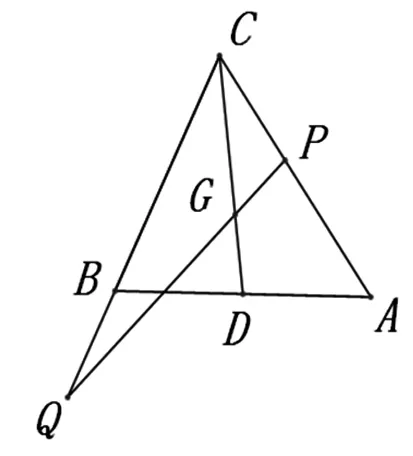
图6

点评：本题若直接求解，不但难度大，而且计算量也大，求解过程十分繁琐，从而导致求解困难.而直接应用三点共线向量定理求解，不仅降低了难度也简化了计算，求解过程显得十分简洁.

例4 (2018届武汉5月调考理科第16题)已

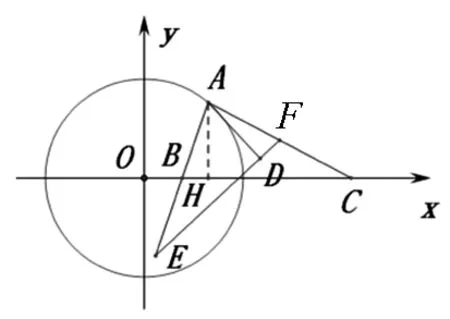
图7

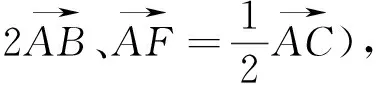
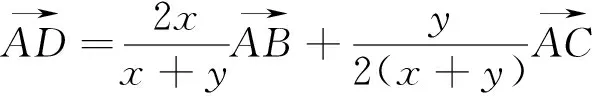
教材中的例习题一般都具有典型性、代表性、示范性，对课本上一些看似平谈无奇的例(习)题进行深入的探究，可能有着意想不到的结果与功能，让学生在学到知识的同时，掌握隐藏在其背后的思想方法、定理，活跃学生的思维、拓广其思路，提高解题能力，收到事半功倍的效果.