2018年高考数学全国卷Ⅲ文科20题探究*

四川内江师范学院数学与信息科学学院 (641112) 胡生兵 赵思林

一、试题再现

题干中的线段AB实质上是考生非常熟悉的中点弦，第(2)小题以向量的形式呈现．此题以数学核心素养立意．内涵深刻，含有教材背景，解题思路宽，具有较高思维训练价值，值得探究．下面对这个优秀的题目，从试题的立意、试题背景、试题解法和解题启示等方面作一些探究．

二、试题的立意

立意是试题考查的目的．高考数学命题，在考查基础知识的基础上，注重对数学思想方法的考查，注重对数学能力的考查，展示数学的科学价值和人文价值[1]．本题以数学核心素养立意，意在考查解析几何的基本思想方法(即解析法)和向量的基本思想方法(即向量法)．下面从考查基础知识、数学思想方法、数学能力等方面分析试题的立意．

以知识立意：本题考查了直线的斜率、椭圆方程与性质、直线与椭圆的位置关系、平面向量的运算、三角形重心性质等数学基础知识．

以考查数学思想方法立意：本题考查了转化与化归、数形结合等思想，并考查直线与椭圆的交点、线段长度的求法，用中点坐标表示斜率、判断等差数列等基本方法．

三、试题的教材背景

像这样立足于教材的试题，既可以保证试题背景的公平性，同时可以抑制题海，还对中学数学教学有很好的引导和导向作用．因此，应该大力提倡立足于教材的高考试题．

四、思路分析与解法探究

波利亚曾指出：“掌握数学就意味着善于解一些要求独立思考，思路合理、见解独到和发明创造的题．”对试题的分析和解法探究可以从多角度、多层次思维着手，意在培养学生对不同知识的融会贯通，培养学生数学解题思维的发散性、系统性、优化性、创新性．

(一)第(1)小题的思路分析与解法探究

第(1)小题主要有运用韦达定理、参数法、运用椭圆(或双曲线)的垂径定理、点差法、点差法的优化等方法．

思路分析1：(运用韦达定理)设直线l的方程为y=k(x-1)+m．

点评：韦达定理是解答解析几何问题的常用方法．该方法的思维难度不高，但是对考生的运算素养要求高．在运用韦达定理时，如果直线方程设立不恰当，将会增加计算难度．

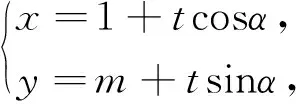
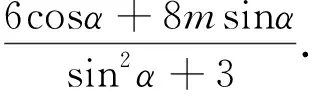
点评：通过构造直线的参数方程，将斜率转为倾斜角的正切值，这样更好地揭示了问题的本质．

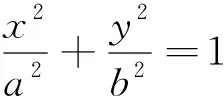
点评：通过题目知道，第(1)问就是考查椭圆的中点弦的相关性质，因此很容易想到运用椭圆(或双曲线)的垂径定理．运用此结论可以降低运算难度，规避繁琐运算．

点评：点差法体现了整体代换的思想．解答问题(1)的关键就在于运用点P的纵坐标表示斜率．根据斜率的定义、又知道中点坐标，所以运用点差法可以减少运算量，使问题轻松获解．

思路分析5：(点差法的优化)在运用点差法时，总共设了四个未知数x1,x2,y1,y2，运用中点坐标减少未知数个数．

设点A(x1,y1)，因为中点M(1,m)，所以点B(2-x1,2m-y1)．将点A,B代入椭圆方程，得

点评：运用中点坐标表示点A，等价于将点A和椭圆进行平移．方程②表示平移后的椭圆，并且椭圆①和②关于点M对称．而直线l表示两个椭圆的公共弦．此方法很好的揭示了问题的几何意义．

(二)第(2)小题的思路分析与解法探究

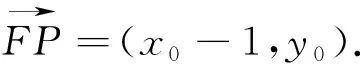
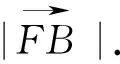
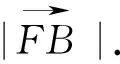
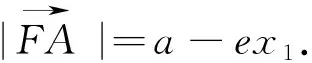
五、教学启示

从高考命题的角度看，此题源于教材、高于教材，所以在平常教学和高三复习中都要重视教材、回归教材、认真钻研教材．此题以数学核心素养立意的意图是明显的，也是成功的．因此，数学教学应精选能体现数学核心素养的好问题，让学生进行深度思考，多角度开展数学探究，不断提高问题分析和问题解决的能力．

解析几何是高考的重点、热点和难点．解析几何之难往往难在其运算素养要求高上，也就是说，运算素养位于解析几何的制高点，运算素养有时决定着解析几何学习和考试的成败．在解析几何中如何降低(减少)运算量或回避繁琐的运算，是解析几何教学应该思考和研究的问题．以本题为例，熟练运用韦达定理，善于借助几何直观，灵活运用直线或椭圆的参数方程、弦长公式以及向量工具等，就可以降低或减少运算量．

数学核心素养与数学思想方法具有密切关系．在解题教学中应重视数学思想方法的运用，如数形结合、转化与化归、分类与整合、方程或不等式等思想的运用，熟练解析法、向量法、定义法、参数法、点差法等数学基本方法的运用，对学生学好数学、用好数学和考好数学都是有益的．