探究代数表示几何量的有效策略——以几道圆锥曲线题为例

浙江省金华市第六中学 (321000) 虞 懿

解析几何的核心方法是用代数的方法研究图形的几何量(长度、角度、面积等)，核心思想是“数形结合”．本文采撷几道典型试题，从解决解析几何问题的核心思想方法出发，着重探究代数表示几何量的有效策略．

一、策略举隅

策略1以点坐标为参数实现几何量的代数表示

分析：“几何量的代数表示”是解决解析几何问题的关键，在本题中的几何量是线段AB的长度，用什么样的代数式来表示这个几何量？解析几何中描述弦长的代数量通常就是点坐标或直线斜率或直线截距等．

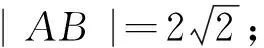
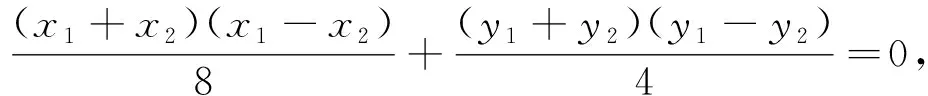
评析：涉及“中点弦问题”时通常采用点差法．所谓点差法，就是在求解与圆锥曲线有关的弦的“中点问题”时用到的一种“代点作差”的解题方法，其特点是代点作差后可巧代直线斜率和中点坐标，进而通过“设而不求”以达到减少计算量的目的．

策略2以直线斜率为参数实现几何量的代数表示

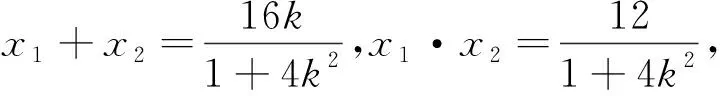
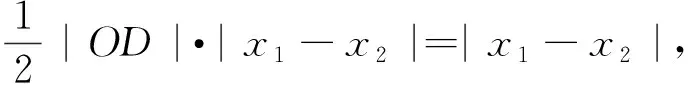
评析：根据条件得出四边形OANB为平行四边形，然后设出直线l的方程，并代入椭圆方程中，从而利用韦达定理得到S四边形OANB的代数表达式，通过换元再利用基本不等式求得其最值．求多边形的面积问题，常转化为三角形的面积后进行求解，这点应格外重视．

策略3以直线截距为参数实现几何量的代数表示

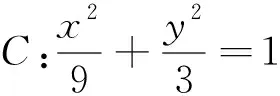
分析：设出直线l的方程，与椭圆方程联立，由判别式、韦达定理和条件OA⊥OB得出k与m的关系，再利用弦长公式及三角形面积公式就可以建立S关于m的目标函数．

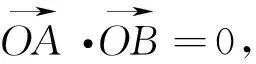
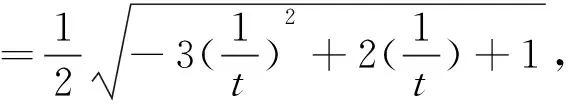
策略4借助参数方程实现几何量的代数表示

图1

(1)求直线AP斜率的取值范围；

(2)求|PA|·|PQ|的最大值．

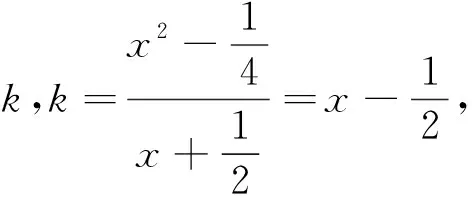
评析：利用直线参数方程中参数的几何意义，避免了繁琐的计算，使得方程的联立简便易得.

策略5回归向量知识本质实现几何量的代数表示

向量具有代数、几何双重身份，融数形于一体，是沟通代数和几何的桥梁．它可以将几何问题坐标化、数量化，因此它是解决解析几何问题的重要工具．

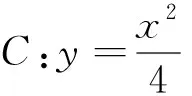
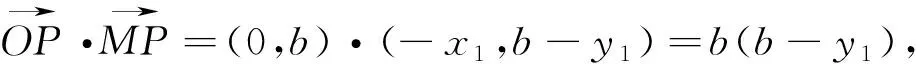
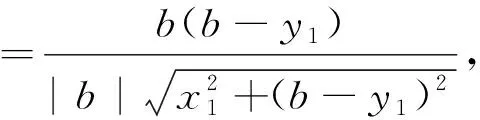
若cos∠OPM=cos∠OPN,有

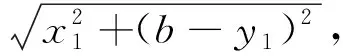
综上，点P(0,-a)符合题意．

评析：本解法另辟蹊径，构建平面向量，利用数量积的定义求夹角，简洁明了．在探究解题思路时，要善于从不同的角度分析、挖掘它与其他知识的联系，在平面解析几何中有关长度、角度的计算及有关平行、三点共线、垂直等位置关系问题都可以用向量知识解决．

二、探究启示

解析几何的核心方法是用代数的方法研究几何问题，在解题过程中，首先要将文字信息、图形条件进行转换，通过代数语言描述几何要素及其关系，将已知的几何量(条件)表示成代数式，然后进行适当的代数运算得出代数结果，最后通过分析代数结果的几何含义解决几何问题，在这个过程中要经历文字信息、图形特征和符号语言之间的多重转换．因此，我们必须重视对几何量(关系)的深入研究，探究用何种代数形式能恰当表示题目中的几何量(关系)，同时有利于代数运算，从而形成正确的求解策略．