解析几何中“任意点和它的对偶直线”在解题中的妙用

江苏南京工程学院 (211167) 尤兴华江苏省南京市第二十九中学 (210036) 尤新建

一、问题的提出

在解析几何中，题型丰富多彩，更需要我们不断加以分析总结，看清题目背后的知识背景，思考问题的核心本质，这样才能通过解决一个问题，掌握一类问题.

极点极线(特殊的点和直线的对偶关系)是高等几何的概念，二次曲线的好多性质都与它有关，许多考题的设计也都来源于此，虽然以前也有好多论述，但好多师生并不熟悉，本文再次加以总结，希望对读者有所帮助.

文[1]论证了圆锥曲线内的点和它的对偶直线的存在性和对应关系，得到了关于对偶点和对偶直线的一系列结论．

结论1 给定圆x2+y2=r2：

(1)P(x0,y0)是不同于圆心的任意一点，则点P的对偶直线是x0x+y0y=r2；

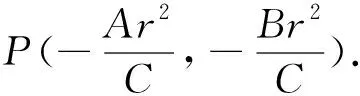
注：若点P在圆上，则其对偶直线为经过点P的圆的切线；若点P在圆外，经过点P引圆的两条切线PA、PB,其中A、B为切点，则其对偶直线为切点弦AB所在直线.

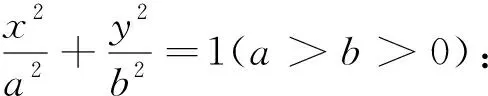
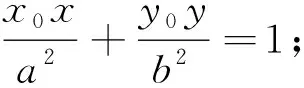
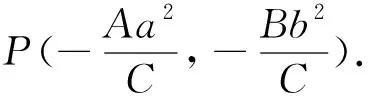
注：若点P在椭圆上，则其对偶直线为经过P的椭圆的切线；若点P在椭圆外，经过点P引椭圆的两条切线PA、PB,其中A、B为切点，则其对偶直线为切点弦AB所在直线.

文[2]对于上述结论给出了部分证明.下面就应用这些结论解决一系列的问题：

二、点关于圆的“对偶直线”的应用

例1 已知圆C1:(x-1)2+y2=16,圆C2:(x+1)2+y2=1,点S是圆C1上的一个动点，设过C2的直线交圆C1于A，B，且以A、B为切点的两条切线交于点Q,求证：点Q在定直线上.

证明：设Q(m,n),则切点弦AB的方程为(m-1)(x-1)+ny=16,将C2(-1,0)代入得到m=-7,故点Q在定直线x=-7上.

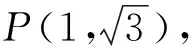
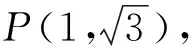
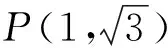
三、点关于椭圆的“对偶直线”的应用

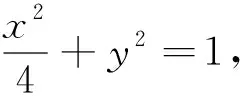
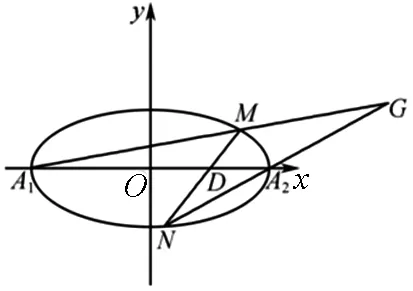
图1

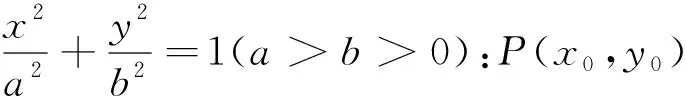
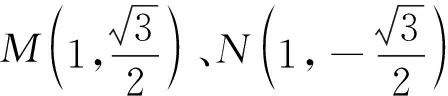
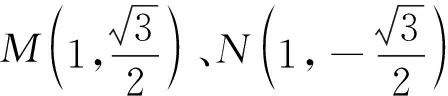
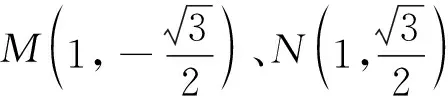
若点G恒在一条定直线上，则此定直线必为x=4.下面证明对于任意的实数m，直线A1M与直线A2N的交点G均在直线x=4上．

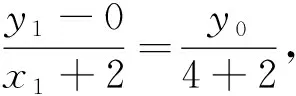
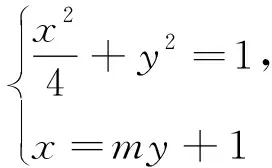
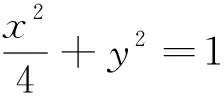
四、追本溯源，链接高考

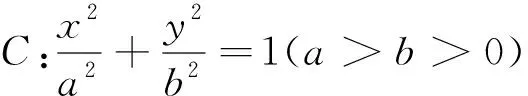
(1)求椭圆C的方程；

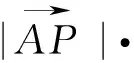
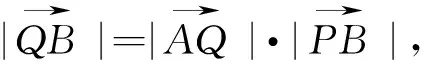
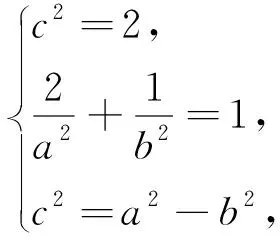
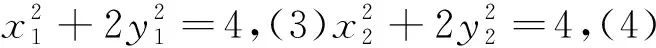
(1)+(2)×2并结合(3)，(4)得4x+2y=4,即点Q(x,y)总在定直线2x+y-2=0上.

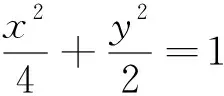
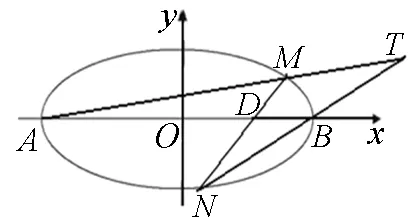
图2

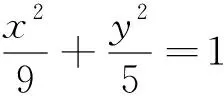
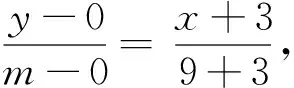
当x1≠x2时，直线MN方程为

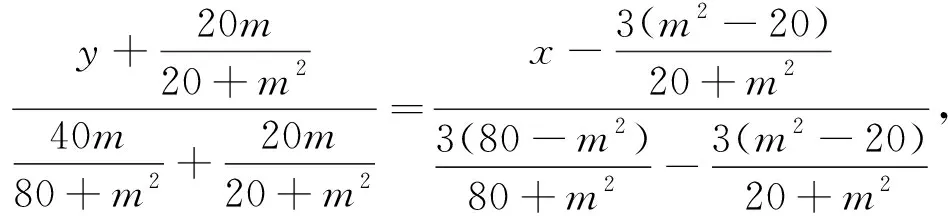
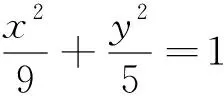
基于核心素养的数学教学强调通过建立适当的数学模型，刻画研究对象的性质，关系和规律，数学教育的根本是培养学生的数学直观，数学的结论是“看”出来的，不是“证”出来的.解析几何在高中数学的地位很重要，学生的普遍问题是算不到最后的结果，无功而返，通过以上几例的比较，试图能够让学生透过一系列的数学现象领略到其背后的本质，建立数学模型，从而很快洞察该类型结果，积累数学思维和实践的经验，在这个基础上促进学生形成和发展数学核心素养.