一道解析几何问题的解法及启示

江苏省常州市北郊高级中学 (213031) 耿晓华

解析几何是一门用代数的方法去研究几何问题的数学分支，因此对运算的要求比较高．学生对这部分内容的学习普遍感到难度较大，原因大致有：对运算策略不够清晰，对算法设计不够明确，对复杂计算畏难畏繁情绪重，运算的意志力不坚定等等．而教师对解析几何的教学难度也是较大的，尤其是解析几何的习题教学．本文以一道解析几何题为例，给出了2种运算策略，4种算法设计(具体体现在4种不同的解法，而思路全部由学生提供)，并结合这道题的教学实践给出了几点启示，以期与同行分享．

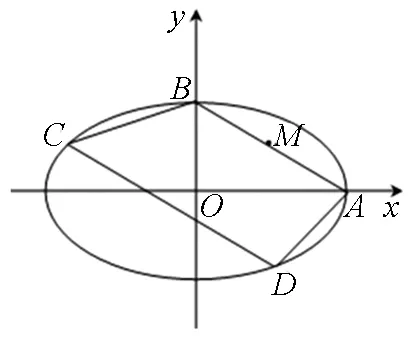
图1

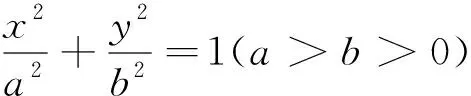
(1)求椭圆的离心率；

(2)已知a=2，四边形ABCD内接于椭圆，AB∥DC，记直线AD，BC的斜率分别为k1，k2，求证：k1k2为定值．

策略1 视k1,k2为已知，用k1表示点D坐标，用k2表示点C坐标，计算出直线CD的斜率，由AB∥DC，得到AB，DC的斜率相等，从而得到关于k1,k2的方程，化简求k1k2．

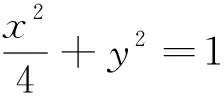
策略2 视k1,k2为未知，用合适的参数表示k1，k2，再计算k1k2．这里合适的参数，可以是直线CD的纵截距m，也可以是点C的坐标(x0,y0)等．

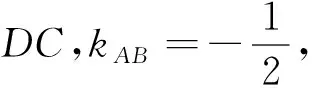
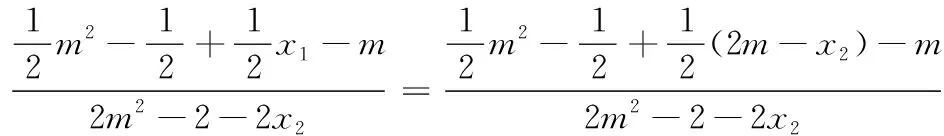
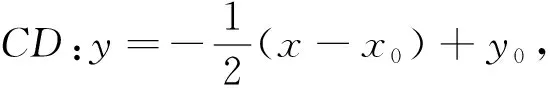
从这道习题的教学实践，笔者得到几点启示．

启示1 解析几何的定值问题的求解要重视运算策略与算法的设计．在这里，可以认为运算策略是比算法更上位的概念，用来表明运算的大致方向．例如，本例中的策略大致有两种，其一视k1,k2为已知量，通过建立等量关系化简求k1·k2，其二视k1,k2为未知量，用合适的参数表示k1,k2，再求k1·k2．相对与运算策略，算法则更为具体，而且步骤明确．算法的效率也有高低之分，高效的算法步骤少，每一步运算容易，而低效的算法步骤相对长，有一些步骤的运算比较复杂(比如需要直线与椭圆方程多次联立等)．例如，本题的策略1对应的算法在解法1中得以体现，本题的策略2中参数的选择有多样性，算法也是多样的，具体体现在解法2-4上．解法1中需要两次联立分别求点C，D的坐标，然后根据斜率相等得到等式并因式分解，再证明其中的一个因式不为0(这个证明也是不容易想到)，从而得到结论，这种算法虽然想法自然，但是运算效率不高．解法2-4中都用适当的参数表示k1·k2，其中解法2的参数选择了直线CD的纵截距m，解法3中的参数选择了点C坐标(x0,y0)，尽管有两个参数x0，y0，但是它们满足椭圆方程，是具有关系的两个参数；解法4中的参数选择了点C，D的四个坐标分量，但这四个参数满足三个方程，于是可以通过方程的变形进行整体消参．解法2和解法3都需要联立直线方程和椭圆方程一次，比解法1的运算效率要高，而解法4不需要方程的联立，对方程的变形要求很高，但运算的效率也非常高．教师如果在解析几何的习题教学中常常引导学生思考运算策略和算法，学生逐渐形成良好的思维习惯，运算的算法设计好之后经过简单地比较，选择运算效率高的算法，这样会避免运算的盲目性，提高正确率．

启示2 注重对解析几何中定值问题结论的反思，从结论是否能够推广和变形的角度引导学生思考，思考能否可以得到有趣的一些结论．这样的引导有利于培养学生的反思能力，以期解一道题，明一组题．

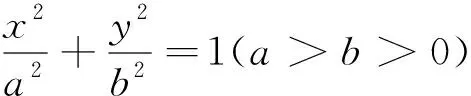
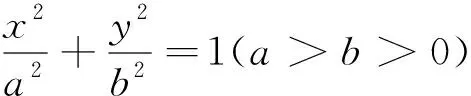
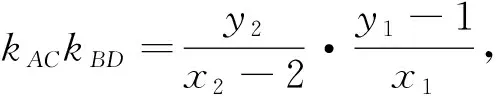
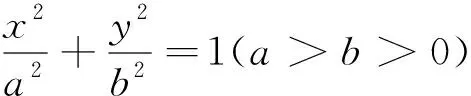
从原来的问题可以衍生出这样两个有趣的一般结论，而在解析几何的问题中常常会出现这样的情形．教师适当地引导学生探究，会逐步培养学生不断探索问题的意识，逐步养成依照观察、猜测、证明的流程发现新的结论的能力，这对学生的数学素养的提高大有裨益！

启示3 注重对解析几何中定值问题的结论的反思，引导学生能否分析其背景，这样会让学生加深对问题本质的理解，同时能够从更高的视角去认识问题．

例如，上述题目可以认为是下列背景问题，经过伸缩变换得到的：

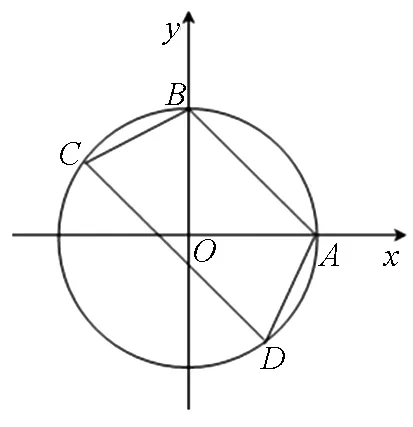
图2

背景问题如图2，设圆x2+y2=a2(a>0)与x轴的正半轴的交点为A，与y轴的正半轴的交点为B，四边形ABCD内接于圆，AB∥DC，记直线AD，BC的斜率分别为k1，k2，则k1k2=1．

这个结论很容易得到，明显直线AD，BC关于直线y=x对称，因此它们的倾斜角互余，所以k1k2=1．同样直线AC，BD的倾斜角也互余，则AC，BD的斜率乘积也为1．

高中阶段只介绍了伸缩变换的概念，对于它的性质及运用并没有深入研究，因此用伸缩变换的性质来解决问题或许超过了高中学生的知识范畴．事实上，由于椭圆与圆之间的联系，很多椭圆的试题就是改编自圆的一些结论，教师如果能适时地揭示它们的关系，还原问题本来面目，弄清它的本质，可以让学生站在更高的视角去看问题．