“微变革、微创新”视域下的课堂微探究*

广东省湛江市第二十八中学 (524033) 梁成培广东省东莞市麻涌中学 (523000) 骆妃景

1.微探究背景

教学中一线教师一直强调教材例题、习题的重要性.因为现在很多高考真题、模拟题都是对教材中的典型例题、习题的改编，源于教材，高于教材.因此教师要引领学生在解决问题后，对该问题做进一步的微探究、微反思，挖掘其中的教学价值.微探究是课堂上根据教学内容、围绕某个知识点或某一问题，在教师的组织、引导下，让学生以自我探究或合作交流的方式学习.教学中教师从考点、学生学习的疑点、难点等微问题进行微探究，适当穿插微专题进行协同教学，对数学有事半功倍的效果，助推学生和教师共同成长.所以笔者认为在高考备考中应注重微探究.下面以2018年东莞市二模理科数学第20题为例，从高三学生的认知水平出发，引导学生题源追溯，从多视角进行微探究，微推广，并结合笔者自身微探究教学实践与体会，提出了两点高三数学备考建议，希望能给同行起到抛砖引玉的作用.

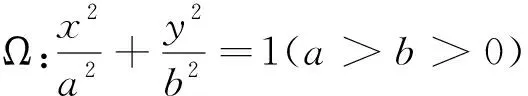
(1)求椭圆Ω的标准方程；

(2)设直线l′交椭圆Ω于C,D两点，且OC⊥OD，求证：O到直线l′的距离为定值.

1.1 思路分析

1.2 试题解答

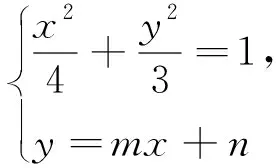
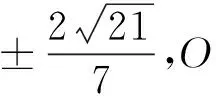
若此题讲评后，教师就认为问题解决了，没有引领学生进行反思总结，就无法进一步挖掘题目的教学价值，发现知识本质.而在数学学习中，把握知识的本质源头才能以不变应万变.著名数学家波利亚提出，解数学题就像采蘑菇一样，当我们发现一个蘑菇时，在它周围可能有一个蘑菇团.鉴于此，笔者在课堂上提出两个问题：

(1)我们平时探究定值问题时是怎样找定值的呢？

(2)这个定值是巧合，还是蕴含着一种规律呢？

此时，学生的心中已燃起了探究的火花，带着问题，各研究小组进行了探究.

2 题源追溯

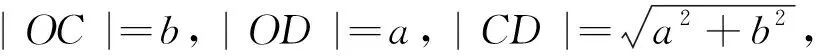
在学生1给出猜想之后，其他学生都露出了好奇的表情，课堂进入了紧张的探究阶段.经过几分钟的自主探究和小组激烈的讨论，第二小组学生2阐述了小组共同的探究成果.

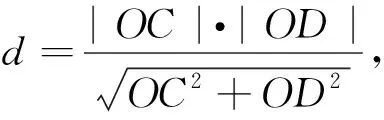
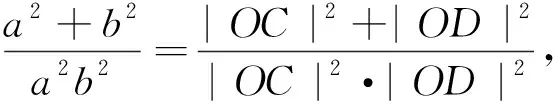
试题2 (人教A版《数学》选修4-4)第15页习题1.3第6题)已知椭圆的中心为O，长轴短轴的长分别为2a、2b(a>b>0)，A，B分别为椭圆上的两点，且OA⊥OB.

(2)求ΔAOB面积的最大值和最小值.

3 微探究

试题2实际上是极坐标参数方程中一个非常典型的极坐标方程应用问题，其内涵丰富、证明方法多样、思想深远.

第三小组学生3也不甘示弱地站起来证明第1问,并从第2问中得到启发,发现m|OA|2+n·

|OB|2(m>0,n>0)的最小值也为定值.

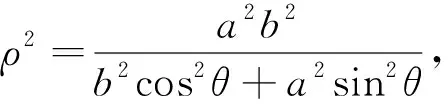
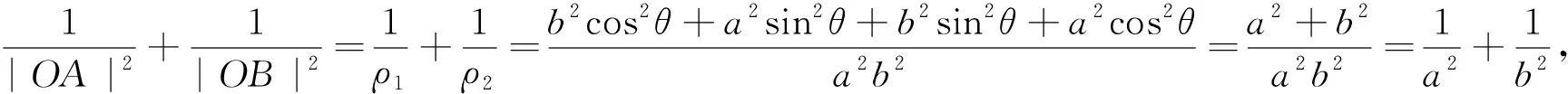
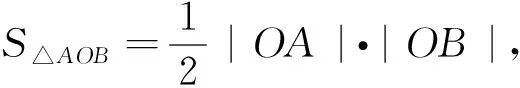
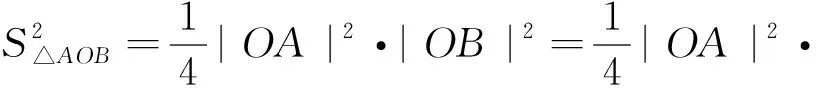
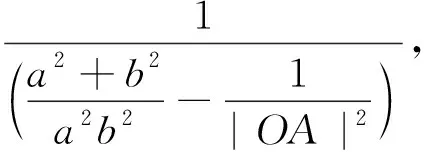
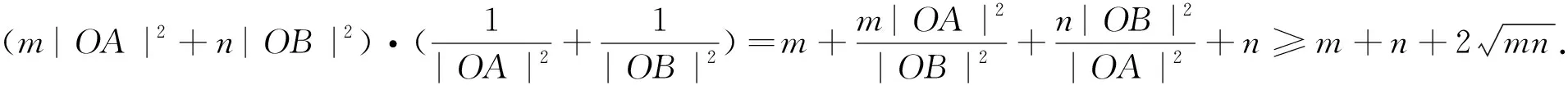
此时，全班再次响起了雷鸣般的掌声.

多么自然的想法，多么合理、恰当的知识迁移，学生们的探究精神在课堂上得到淋漓尽致的体现，数学核心素养得到了很好的培养.

笔者大力表扬以上三位学生后，引导全班同学对刚才三位同学的结论进行总结.第四小组的学生4早已兴奋不已，急忙站起来归纳，脸上笑容甚是灿烂.

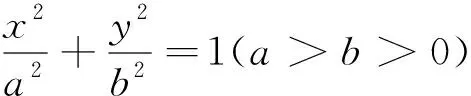
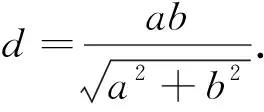
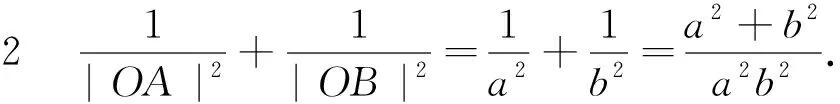
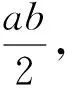
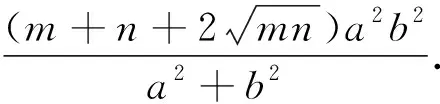
实际上，问题到这里已经得到了深度挖掘，探究的目标已经达到.但此时任何力量也阻止不了学生继续探究的欲望和创新的激情.

于是，笔者继续引导学生进行探究，根据我们以往的学习经验，椭圆与双曲线的性质是类似的，椭圆中有以上四个定值、最值结论，那么双曲线中是否会有类似的结论呢？若有，又会是怎样呢？

全班学生类比刚才的探究方法继续钻研，过了几分钟，第5小组的学生5又将双曲线中的定值结论向全班同学进行了正确的微推广和证明(证明略).

4 微推广

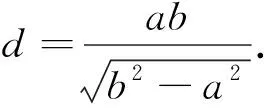
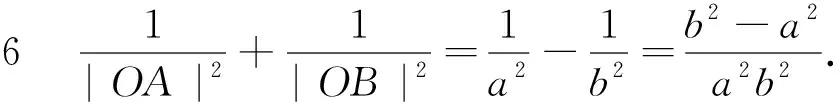
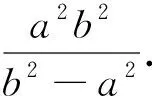
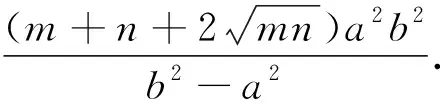
到此，全班同学的掌声一浪高过一浪，学生仍然意犹未尽，仍想继续探究，于是笔者鼓励学生在课后小组间继续合作探究，以期探究出更多隐藏在圆锥曲线中的定值、最值问题！

5 备考启示

笔者经常在课堂上引领学生解决问题后，再对问题进行微探究、微反思，在微探究教学实践中得到以下2个方面的备考启示.

5.1 潜心研读教材，把握知识本质

高三数学资料随处可见，数学教学的题海教学也比比皆是，笔者回头梳理了本节课试卷讲评的探究历程.最大的感触就是在高考备课中要十分重视教材中的任何一道题目，教材是专家经验的积累，智慧的结晶，因此每道例题、习题都有其教学的价值，教师要学会引领学生对其进行深度研究.近年来，很多高考题、模拟题都是源于教材、高于教材，比如2016年全国I卷中理科数学第4题的几何概型问题与人教A版必修3第136页例1很相似；试卷中第16题与人教A版必修5第87页简单的线性规划问题的引例如出一辙.所以教材永远都是命题的本源，教会学生利用好教材，善于积累将会对高考备考起到事半功倍的效果.

5.2 微探究培养思维，凸显数学学科素养

高三备考中要重视学生的思维训练、课堂上注重对微知识、微问题进行微探究，培养学生学科素养.不能让学生在“茫茫题海”中“随波逐流”.作为教师应该要授人以渔，教给学生更多分析问题、探究问题的方法和培养学生解决问题的能力，而不应该反复机械的做题.著名数学家波利亚曾经说过：“在你找到第一个蘑菇时，继续观察，你就能发现一堆蘑菇”.从高考真题、模拟题、教材例题习题的微探究过程来看，学生解决了一个又一个问题，发现一个又一个结论，实际上这就是探索、发现的过程，是在培养解决新问题的能力，也是在不断提升数学的学科素养.