重视解题反思 提高应对能力
安徽淮北师范大学数学科学学院 (235000) 谢舒婷 张 昆
高考数学作为高考中的重点科目之一,在每一年的“高考季”都会引起社会各界的广泛关注,这与数学在人类社会中的地位是分不开的.数学在形成人的理性思维、科学精神和促进个人智力发展的过程中发挥着不可替代的作用.但由于数学学习对象的抽象性,数学活动的探索性,数学推理的严谨性和数学语言的特殊性都决定了思维正处于发展阶段的中学生不可能一次性地直接把握数学学习的本质,必须要经过多次反复探究、深入思考、自我调整,即坚持反思性数学学习,才可能洞察数学活动的本质特征.[1]那么,如何在解题学习与训练中提高自己独立解题能力,从而应对新的问题呢?
一、反思解题活动中涉及的知识
就大多数学生而言,对某一个数学对象的认识,不是在一次数学活动中就能完成的,每一次数学活动都可能提供对某一个数学对象提高认识水平的机会.特别是,虽然同一数学对象在不同的情境下表现出的非本质特征不尽相同,但是其本质特征确实不变的.经过多次内容类似的数学解题活动,对于已得到的某些结论的正确性会更加的自信,这种自信得益于在解题活动中得到的“实验性证据”.换句话说,在几次遇到相似的题目,通过对解题过程的反思,学生也许会察觉出潜藏在其中的一些普遍的方法.下面来看两道高考数学中的函数压轴题.

(1)讨论f(x)的单调性;

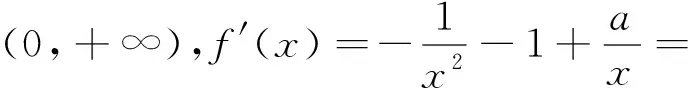
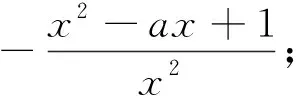
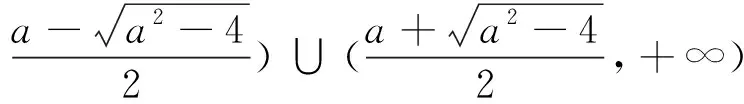
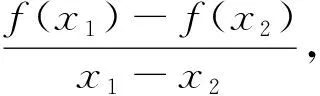
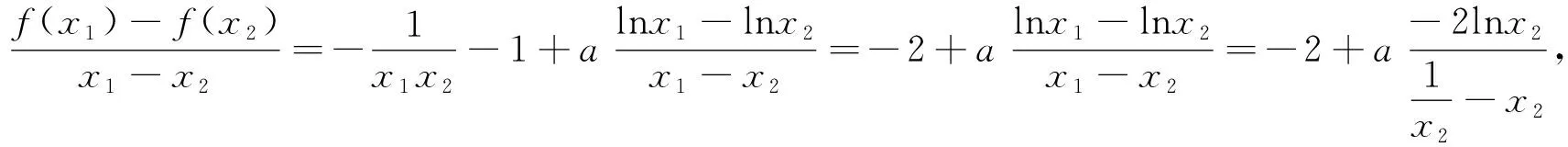
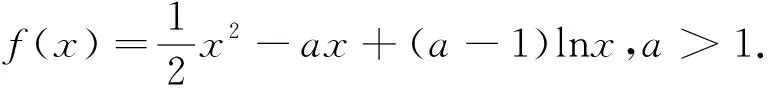
(1)讨论函数f(x)的单调性;
(2)证明:若a<5,则对任意x1,x2∈(0,
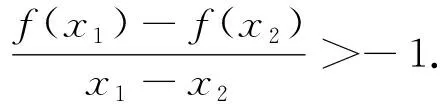
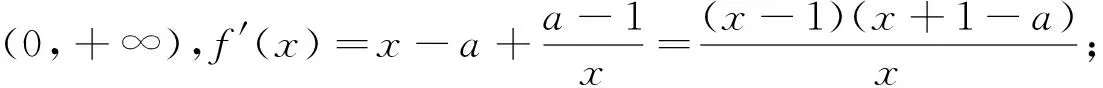
考题分析:上述两道题目中,(1)均是讨论函数单调性问题;(2)均是以中值定理为背景,虽然题目不是完全相同,但确实是属于同一类经典题型的展现.反思整个解答过程,并联系以往解决类似问题的经验,可以总结出解答(1)类问题的四步骤:
①在求出原函数的导函数后,判断导函数的类型;②判断此导函数方程根的存在性;③如果导函数方程的根存在且有两个,则判断两根的大小关系;④观察定义中是否涉及到区间端点,则判断根与区间端点的位置关系.
两道题目的(2)问,在解题时均是对目标等式进行移项、通分、构造出新函数;再关注新函数的单调性(单调递减),最后利用(1)中参变量的取值范围就可以快速破解.
函数的多种性质中,单调性是其最重要的性质之一,高考的压轴题也常常是以考察函数单调性为中心.在其他的高考函数压轴题上多是以考察函数性质为基点,再为其加上一些美丽的“包装”,无论是极值点偏移问题、双变量问题或双零点问题,其方法都是相通相似的.
在解答过例1再解答例2时,会自然的想到“这里有一道题目和你的题目有关并且以前解过”,应用某道之前解过的题目的意图会影响到对新题目的考虑,因此会试图将新旧两道题目联系起来,根据旧题目中某些重要的因素为新题目引入类似的因素.比如在寻找例2(2)问的解题思路时,会发现当完成去分母,移项后得到了“f(x1)+x1>f(x2)+x2”,此时根据对例1中知识点运用的反思,而想到接下来依然可以通过构造新函数,将题目转化为判断新函数单调性的问题.这时,构造新函数“g(x)=f(x)+x”的想法自然而然的就会迸发出来.因此,数学知识是解题的基础,而解题过程也正是展示知识之间联系的有效途径,反思解题中所用知识点及知识点间的联系,有助于加深对知识间关系和联系的认识,使头脑中的知识网络向横纵向展开,知识结构得到扩充,以此提高解题活动中的应对能力.
二、反思解题活动中对题意的理解过程
就学生的解题活动而言,“理解题意”无疑是首先要学习的.很多学生找不到解题途径的根本原因,正是”理解题意“这一环节存在问题.信息论观点提出理解题意就是从问题的情境中“如何获取信息”和“如何加工信息”,因此要求学生对自己理解题意的过程进行反思,实际就是要求他们对自己“获取信息”和“加工信息”的过程进行思考.
例3 (2018全国Ⅰ卷20)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验.设每件产品为不合格品的概率为p(0 (1)记20件产品中恰有2件不合格品的概率为f(p),求f(p)的最大值点p0. (2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p0作为p的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用. (ⅰ)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X,求EX; (ⅱ)以检验费用与赔偿费用和的期望值作为决策依据,是否该对这箱余下的所有产品作检验? (1-p)17(1-10p).令f′(p)=0,得p=0.1.当p∈(0,0.1)时,f′(p)>0;当p∈(0.1,1),f′(p)<0.所以f(p)的最大值点为p0=0.1. (2)由(1)知,p=0.1. (ⅰ)令Y表示余下的180件产品中不合格品件数,依题意知Y~B(180,0.1),X=20×2+25Y,即X=40+25Y.所以EX=E(40+25Y)=40+25EY=490. (ⅱ)如果对余下的产品作检验,则这一箱产品所需要的检验费为400元.由于EX>400,故应该对余下的产品作检验. 考题分析:首先,(1)问解题的关键点就在于是否能清晰的理解题意所述内容,判断出其为二项分布还是超几何分布.通过对题意分析可知,本题为二项分布,接着便可以根据二项分布的特点列出关于p的函数式.其实概率统计类型题目与“二三四”是分不开的:“二”即两大概型:古典概型、几何概型;“三”即三大分布:二项分布、超几何分布、正态分布;“四”即四个图表:频率分布直方图、散点图、茎叶图、列联表.用这三个连续自然数概括出的结论构成了概率统计的核心骨架. 其次,此题的概率统计还同导数相结合,当涉及“何时取得最大值”,自然想到要对关于p的函数进行求导,其实(1)的本质也是对极大似然概率思想的考察.最后,(2)的问法相对比来说也较为传统,与2016年全国Ⅰ卷19题(3)中“判断在哪一点处期望值最优”思想如出一辙. 反思理解题意的过程,一般从熟悉题目到深入理解题目,在这两个环节中都应抓住以下几个关键问题: (1)“我应该从哪里开始?”当出现间隔一段时间不去看题目都不会忘掉它时,便说明对题目的叙述已经很清楚了,并能在头脑中留下深刻的印象; (2)“我能做什么?”将题目的主要部分分离出来.“证明题”中寻找前提和结论,“求解题”中则寻找未知量、已知量和条件,依次对它们进行考虑,并以不同的方式组合起来加以考虑,把每个细节同其他一些细节以及每个问题同整个题目联系起来; (3)“这样做我能得到什么?”此处可能会产生一个可以直接解答的念头,但是也可能需要产生更多有用的念头,在这些念头中有些可能会将思路引入歧途,但是这些念头无论是次要的、模糊的,还是明确的,它们都可能使你对题目的概念有一个更完整、更有条理、更和谐或更平衡的看法. 因此尤其要对那些有过反复曲折过程的问题,进行反思.通过这样的反思,学会在理解题意方面寻找规律,积累更多的经验. “没有任何一个题目是彻底完成了的,总还会有些事情可以做;在经过充分的研究和洞察以后,我们可以将任何解题方法加以改进;而且无论如何,我们总可以深化我们对答案的理解.”[2]每一次数学活动都可能提供对某一个数学对象提高认识水平的机会,通过对每一次数学解题活动的反思,将认识“活”起来,使其成为能够迁移的认识,能在新的问题情境下加以运用的认识,这才是真正有用的认识.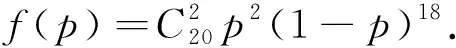
三、结语

