拆解高考数学压轴题教学应用一例
江苏省南京外国语学校仙林分校 (210046) 魏安龙
高考数学试卷中的压轴题往往都是难题中的难题,但是具有较高的教学价值.学生怕做,教师不愿意讲.在这样的情况下,试题的价值除了考试选拔功能外其教学价值就很难得到发挥.为了有效的利用高考压轴题的教学功能,充分发挥试题的指导以及复习价值,本人尝试将高考压轴题进行拆解,根据试题的知识方法背景,编制出一组由易到难的题组,低起点,高输出.这样的拆解,化难为易,由易到难,教师选择以后,可以适合于所有学校所有层次学生的教学.还难题于教学,还难题于本来面目.
一、试题
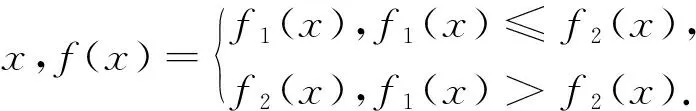
(1)求f(x)=f1(x)对所有实数x成立的充分必要条件(用p1,p2表示);

这是2008年江苏高考数学试卷最后一题,即第20题.

图1
二、试题的拆解
问题1 画出函数y=|x-1|的图像,并写出其单调区间及其对应的单调性.
简解:(方法1)分类讨论;方法2:直线y=x-1翻折;方法3:y=|x|平移.
参见示意图1.
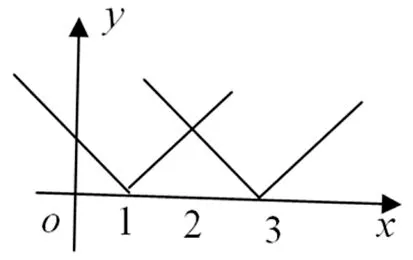
图2
问题2 在同一坐标系中画出f1(x)=|x-1|和f2(x)=|x-3|的图像,并写出函数h(x)=

简解:参见示意图2,(-∞,1),(2,3)减,(1,2),(3,+∞)增.

图3
问题3 在同一坐标系中画出f1(x)=3|x-1|和f2(x)=3|x-3|的草图,并写出函数h(x)=

简解:参见示意图3,(-∞,1),(2,3)减,(1,2),(3,+∞)增.
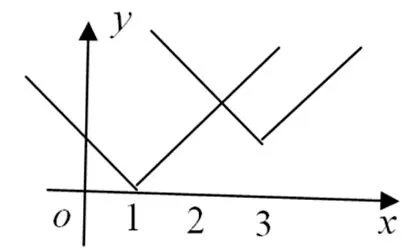
图4
问题4 如果f1(x)=|x-1|和f2(x)=1+|x-3|,定义函数h(x)=

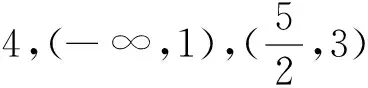
问题5 如果f1(x)=3|x-1|和f2(x)=31+|x-3|,定义函数h(x)=
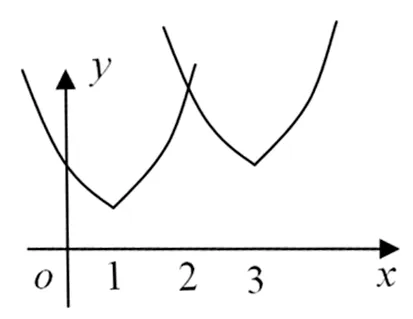
图5

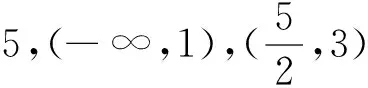
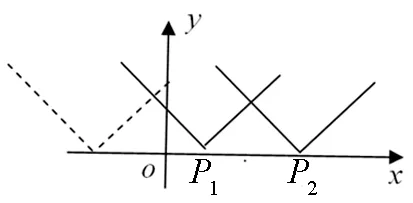
图6
问题6 如果f1(x)=|x-p1|和f2(x)=|x-p2|(p1,p2为常数),定义函数h(x)=

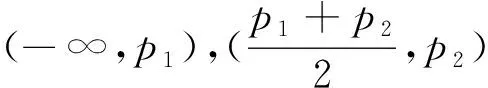

图7
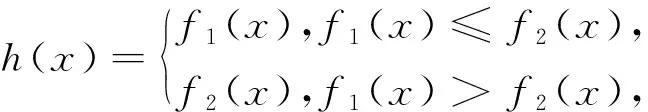
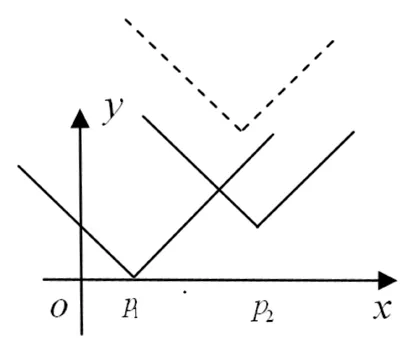
图8
简解:参见示意图7,m≥2.
问题8 如果f1(x)=|x-p1|和f2(x)=m+|x-p2|(p1

简解:参见示意图8,m≥p2-p1.

图9
问题9 如果f1(x)=3|x-p1|和f2(x)=3m+|x-p2|(p1

简解:参见示意图9,m≥p2-p1.

图10

简解:参见示意图10,log32≥|p2-p1|.
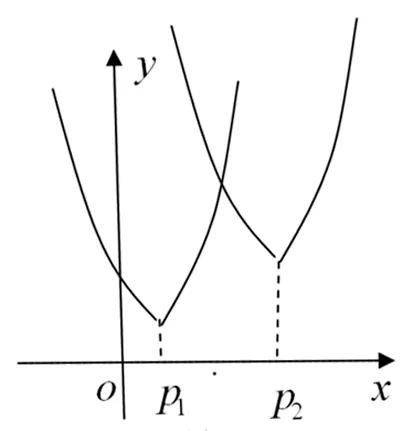
图11
问题11 若已知函数f1(x)=3|x-p1|,f2(x)=2·3|x-p2|(x∈R,p1,p2为常数),函数f(x)定义为:对每个给定的实数x,f(x)=

f(x)=f1(x)对所有实数x成立的充分必要条件(用p1,p2表示).(此题为2008江苏高考第20题(1))
简解:参见示意图11,log32≥|p2-p1|.
问题12 如果f1(x)=|x-1|和f2(x)=m+|x-3|(m>0),定义函数h(x)=

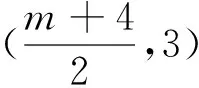
问题13 如果f1(x)=|x-p1|和f2(x)=m+|x-p2|(p1


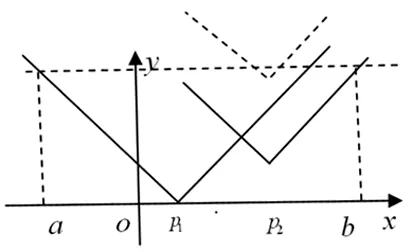
图12
问题14 如果f1(x)=|x-p1|和f2(x)=log32+|x-p2|(p1,p2为常数),定义函数h(x)=
变更分析处理对变更调查的精度和准确性有着直接影响,而重构数据的拓扑关系是这一内业处理环节中的难点之一。在实际应用中,只有部分区域会发生变更,因此,本系统对局部拓扑的方法进行了设计。局部拓扑主要包括增删合并图斑与改变部分图斑的界址点数据2种方式,这2种方式均可促进系统运行效率的提高。

简解:参见示意图12,当log32≥|p2-p1|时,(p1,b)增.当log32<|p2-p1|时,(p1,
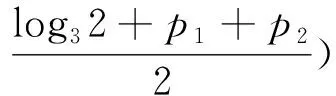

图13
问题15 如果f1(x)=
|x-p1|和f2(x)=m+|x-p2|(p1
设a,b为两实数,满足a 问题16 若已知函数f1(x)=3|x-p1|,f2(x)=2·3|x-p2|(x∈R,p1,p2为常数),函数f(x)定义为:对每个给定的实数x,f(x)= 图14 解:(1)由f(x)的定义可知,f(x)=f1(x)(对所有实数x),等价于f1(x)≤f2(x)(对所有实数x)这又等价于3|x-p1|≤2·3|x-p2|,即3|x-p1|-|x-p2|≤3log32=2对所有实数x均成立.(*) 由于|x-p1|-|x-p2|≤|(x-p1)-(x-p2)|=|p1-p2|(x∈R)的最大值为|p1-p2|,故(*)等价于3|p1-p2|≤2,即|p1-p2|≤log32,这就是所求的充分必要条件. (2)分两种情形讨论 图15 图16 f(x)= 在区间[a,b]上,f(x)= 为了让学生在知识能力方面做到站的高看得远,就需要教师在教学过程中,在备课环节做到脚踏实地,从基础开始,从学生的最近思维发展区开始,一步一个脚印.这样稳扎稳打,有利于打牢基础,提高能力.对于具有价值的典型问题,作为教师,作为高考研究者,要做好的一件事情就是抽丝剥茧,让试题现出真容.再通过教学,做到使学生对戴了帽子口罩架墨镜的问题我还认识你!作为教师,需要多角度审视各种题目,尤其是有较高价值的高考试题.走出迷宫需要思想,带领学生走出题海需要教师的智慧!对于高考命题人员来说,他们的做法是从1可以到n,而我们老师需引导学生从n联想到1.

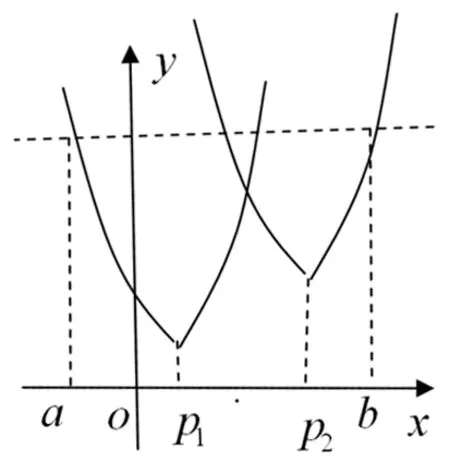

三、原试题的完整解答


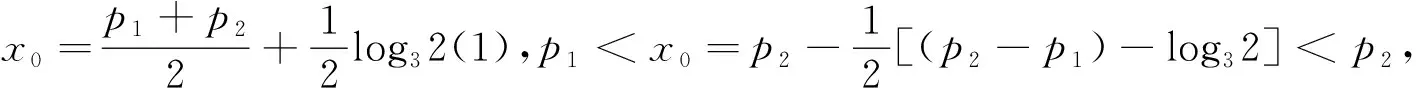


四、感悟与收获

