解题教学讲“推理” 更需讲“道理”——由一道函数的值域求解谈如何进行解题教学

安徽省阜阳市红旗中学 (236000) 潘 静

一、典型案例

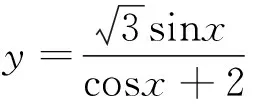
二、问题提出

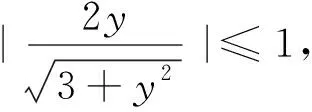
为此，这就要求教师不仅要知其然，而且还要知所以然，在数学教学中，除了教给学生“其然”外，更为重要的是要挖掘出“其然”之中蕴含的“所以然”，俗话说；“事出有因”，因此作为教师必须意识到既然这样做行得通，那么必然有其产生的根源及存在的合理性，事实上教师比学生高明之处，不在于我们教师会解题，而在于我们不仅会解题，而且高屋建瓴，能明白每一种解法的成因如何？因此对于解题思路的来龙去脉，教师要做到清清楚楚，一时不明白，可以请教他人，如果众人“皆醉”，那只有靠自己“独醒”了，此时一定要仔细揣摩，反复斟酌，或许经过一番思考，就会茅塞顿开.

三、剖析成因

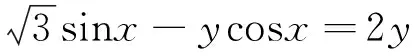
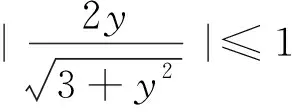
四、教学启示

人们常说：“学习数学的主要任务就是解题”，但笔者认为这种观点不全对，因为数学试题浩瀚如海，怎能做完了？学生只有掌握了解题的思想与方法、解题规律，才能以不变应万变.正如罗增儒教授所言：“数学解题是一种创造性活动，谁也无法教会我们所有的题目，重要的是应通过有限的学习去领悟那种解无限道题的数学机智.”由此可知，学生学习数学的主要任务是“学”解题，为了使学生能在教学中学到解题的秘籍，教师必须明确数学教学的任务是“知其然，更需所以然”，不是为解题而解题，即不在于“解答了多少题”，而在于教师在教学中帮助学生弄清楚了诸如“为什么要这么解？解题思路是如何想到的?”等问题，否则，解题教学就不是真正的数学教学，是伪教学，因为“解”的出发点是答案的正确与错误，关注的是推理过程与结果.而“学解题”的出发点是方法与思维，关注的是思路的成因，即讲道理.”“学解题”是为了学一题会一类的效果.笛卡尔有句名言：我所解决的每个问题都将成为一个范例，用以解决其它问题.”如果教师在解题教学中就题论题，一味采用告诉式的教学，而忽视每种解法背后隐藏的算理的揭示，那么学生掌握的往往是一个个孤零零的题目解法，却未真正掌握解决问题的数学思想方法，举三可能不能反一，试想：学生怎能做到举一反三、触类旁通？

总之，在解题教学中，如果教师直接讲解告知其然，而不探究“所以然”，解题过程虽然无懈可击，学生听懂没有困难，解决类似问题也可模仿，但解答过程似从天而降，过程毫无思维含量，教学过程是教师强加于学生的，题目就变得索然无味，学生不是思维能力提高了，而仅仅是机械模仿套用的能力提高了，到头来，学生学到的并不是真正的数学，因为真正的数学教学是思维活动的教学，不仅是知识传授的教学，更是启迪学生智慧的教学，要充分体现知识发生、形成的过程，充分挖掘解题的思维过程，让学生参与和经历整节课的思维过程，只有这样，教师才能将数学讲懂、讲活、讲深，才能使学生头脑中形成一个具有“活性”的数学知识结构，促使学生数学能力的发展.