以数学文化为载体渗透高中数学隐性知识

陈婉清

[摘   要]近几年的数学高考试题多考查学生对知识深层的本质理解，而非表面的理解与复杂的计算。对数学本质的挖掘成为高水平数学教师在数学教学中必须掌握的要点和必须教授给学生的技能。这部分知识往往是课本中没有具体提及的“隐性知识”。学习数学文化是培养学生数学素养的重要途径，以“数学文化”为载体渗透高中数学“隐性知识”，不仅可以提高课堂的趣味性，还可以帮助学生更好地了解数学，提升数学素养。文章以人教A版高中数学教材选修2-1中“椭圆”的教学为例，以数学文化为载体，讲述高中数学隐性知识。

[关键词]隐性知识;数学文化;圆锥曲线;椭圆

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2019）36-0042-04

一、引言

（一）隐性知识

世界经济组织（OECD）在《以知识为基础的经济》的报告中，将知识分为四类：关于事实的知识（Know-what），关于原理的知识（Know-why），关于如何做好知识（Know-how），关于信息、来源的知识（Know-who）.将前二类称为显性知识（explicit knowledge），后二类称为隐性知识（tact knowledge）.[1]

为了更好地学习隐性知识，相应地把隐性知识分为易于显性化和不易显性化两大类.心理学上已经有证据表明，内隐学习在一定程度上具有可理解特性.[2]这就为隐性知识显性化提供了理论基础.

中学数学中的隐性知识包括课本上没有提及的基本知识;基本思想方法;基本活动经验及经历过程中的感受等方面的获得等.数学教师在教学过程中应充分重视学生对隐性知识的学习，因为，让学生掌握数学的本质是教学良性发展的保障.

（二）数学文化

“数学文化”一词的内涵，简单说，是指数学的思想、精神、方法、观点以及它们的形成和发展;广泛些说，除上述内涵以外，还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等.[3]数学文化无论对于深刻认识作为科学的数学本身，还是全面了解整个人类文明的发展都具有重要意义.

《普通高中数学课程标准（2017年版）》中对高中数学课程性质的定位写道：“数学承载着思想文化，是人类文明的重要组成部分.”数学文化是在数学知识的发展过程中形成和沉淀的.将“数学文化”这一要素加入中学数学教育教学中，有利于学生更好地了解与理解数学.

关于怎样“提升学生的数学素养，引导学生学会用数学的眼光观察世界、用数学思维思考世界、用数学语言表达世界.”这一问题已经成为数学教育行业热议的问题.在数学课程中“突出数学主线”，凸显数学的内在逻辑和思想方法;精选课程内容，处理好数学核心素养与知识技能之间的关系，强调数学与生活以及其他学科的联系，提升学生应用数学解决实际问题的能力.同时注重数学文化的“渗透”，那么，关于“怎样学好数学”和“数学知识的来源”这两类属于数学隐性知识的部分，就可以作为凸显数学的内在逻辑和思想方法的载体，在数学课程中是必要的，也是非常值得教育工作者进行研究的.

（三）以数学文化为载体，渗透高中数学隐性知识的重要性

一个好的数学教师的标准之一，就是把教材中没有编写出来的数学知识（隐性知识）教授给学生，在高中阶段以“数学文化”为载体去渗透数学知识，具有很好的可执行性.从学生的角度看，一方面，学生在了解数学知识的形成、发展过程中，可以更透彻地了解所学知识，从而树立学好数学的信心，喜欢上数学.另一方面，高中作为与大学衔接的阶段，数学作为科学的“皇后”，大多数数学知识理论的形成与发展，是在各个学科的发展过程中根据需要逐渐形成的.通过数学文化的渗透，学生可以了解到自己感兴趣的地方，进而为继续学习做好铺垫.从教师的角度看，一方面，在教学活动过程中，“教什么”要比“怎么教”重要，因为教学内容决定教学形式，教师如果在教学计划中将教材里的隐性知识同教学内容融会贯通，对于数学教学会是一个质的飞跃.另外，“给学生一杯水，老师要有一桶水”.教师在数学隐性知识显性化的过程中，自己必然要了解得更多，站在更高的知识角度，尽可能去发掘數学知识中的隐性知识，并且将这些知识以恰当的方式呈现给学生.这对于教师来讲，是一个成长过程.另一方面，在课堂中，穿插讲授数学文化，可以增强数学课的趣味性，提高课堂教学效率，从而达到事半功倍的效果.

二、教材中与椭圆有关的知识点

本文从人教版A版高中数学教材选修2-1第二章圆锥曲线方程“椭圆”这节内容出发，以从课本中发现本节课存在的“隐性知识”为出发点，以“数学文化”为载体来补充椭圆的教学知识.

（一）教材中的知识安排

从本节人教版教材编写的顺序来看，将“椭圆”安排在选修中，继必修二学习过在坐标系下建立直线与圆的方程，以及在本章节的第一节研究了一般曲线与方程的关系之后，引入椭圆及其标准方程和其简单的几何性质.

教材以一个探究的旁白（如图1）引入椭圆的第一定义，根据所得的椭圆几何特征来选择适当的坐标系，建立椭圆的方程，进而给出了椭圆的标准方程：[x2a2+y2b2=1（a>b>0）]或[y2a2+x2b2=1（a>b>0）].在给出椭圆标准方程后，教材以标准方程：[x2a2+y2b2=1（a>b>0）]为例来研究椭圆的几何性质.

（二）教材知识内容的局限性

教师设计教学进程，往往逃脱不了教材的限制，可借助多媒体展示天体中行星或者卫星的运动轨迹引入椭圆的概念.通过实验或课件演示教材中椭圆的形成，将椭圆从现实生活拉到数学世界.接着教师根据教材中所给出来的椭圆的第一定义，引导学生运用第一节所学的求一般曲线的方法来得到椭圆的标准方程，万变不离其宗.

但从学生对椭圆的理解程度来看，其并没有很好地理解椭圆的“本质”，只是单纯地识记了标准方程[x2a2+y2b2=1（a>b>0）]和一些简单的性质.2008年，浙江高考理科数学第10题困扰了许多学生，这也说明了学生对椭圆存在着本质上理解的不足.

如图2，AB是平面[α]的斜线段;A为斜足，若点P在平面[α]内运动，使得[ΔABP]的面积为定值，则动点P的轨迹是（ ）.

解决这道题的关键是到直线AB的距离为定值的点的轨迹是圆柱面，而圆柱面被斜平面所截的截线当然是椭圆.这就暴露了教材中没有明确讲出圆锥曲线最初是由圆锥或圆柱的截面得到的，学生头脑中并没有将椭圆的生活表象与椭圆的解析几何表象联系起来.[4]

三、对“椭圆”中隐性知识的挖掘

（一）隐性知识：圆锥曲线的起源

关于圆锥曲线的起源有两种说法，一种是在制作日晷中（如图3所示），随着太阳的移动，圆形晷盘上晷针影子尖端形成的曲线就是圆锥曲线.另一种说法与“倍立方”问题有关，公元前5世纪，古希腊数学家希波克拉底将“倍立方”问题归结为求二次比的问题：对一个棱长为[a]的立方体，在[a]和[2a]之间确定[x和y]，使得[a：x=x：y=y：2a].用现在的数学语言来讲，就是要同时解下面三个方程中的两个：[x2=ay，y2=2ax和xy=2a2]，前两个是抛物线方程，第三个是双曲线方程.[5]

圆锥曲线出现在公元前4世纪，柏拉图学派的梅内克缪斯在解决“倍立方”问题时研究了圆锥曲线的性质.他用垂直于母线的平面去截顶角分别为锐角、直角和钝角的正圆锥，得到椭圆、抛物线和双曲线的一支（如图4所示）.

再来看教材章节开头目录中的图片（如图5所示），这其实就是阿波罗尼斯（Apollonius，约公元前262-公元前190）所定义的圆锥曲线，他将圆锥曲线定义为：用一个平面去截一个圆锥面，得到的交线就称为圆锥曲线.在他的著作《圆锥曲线论》中，圆锥曲线也称为“圆锥截线”，严格来讲，被截的圆锥面有正圆锥面或斜圆锥面，得到的交线除了圆、椭圆、双曲线和抛物线外，还包含三种退化情形（一条直线、一个点、两条相交直线）.

关于阿波罗尼斯，他是第一个依据同一个（正的或是斜的）圆锥的截面来研究圆锥曲线理论的人，也是第一个发现双曲线有两支的人.其所著的《圆锥曲线论》（Conic Sections）共八篇，最后一篇已失传.前三篇主要是欧几里得关于圆锥曲线的失传著作的内容，包括梅内克缪斯（Menaechmus，约公元前380-公元前320）和阿基米德（Archimedes，公元前287-公元前212）在这方面的工作.阿波罗尼斯在前人的基础上去粗取精，按照欧几里得《几何原本》公理演绎的方式组织内容，使知识系统化.《圆锥曲线论》含有许多独到和新颖的创造性材料，几乎网罗了圆锥曲线的性质.阿波罗尼斯将欧几里得的几何论证水平发展到极致，使《圆锥曲线论》成为数学史上的一座丰碑，他本人也被称为古希腊“伟大的几何学家”.[6]

在此之后，古希腊后期的数学家帕普斯（Pappus，公元3世纪末）在他的《数学汇编》中证明了椭圆、双曲线和抛物线的焦点-准线性质：到一定點（焦点）及定直线（准线）的距离成一定比例的一切点的轨迹是一圆锥曲线.[5]即我们现在说的圆锥曲线的第二定义或统一定义.

（二）椭圆及其标准方程

1.椭圆定义中的隐性知识

教材中所给的探究旁白中的作图方法其实是16世纪初，意大利数学家蒙特与后来的荷兰数学家舒腾所做椭圆的方法.在这一阶段，人们认识到圆锥曲线并不只是依附在圆锥面上的静态曲线，也是自然界物体运动的普遍形式.德国天文学家开普勒（Johannes Kepler，1571-1630）揭示出行星按椭圆轨道环绕太阳运行，并发现了圆锥曲线的焦点和离心率.[7]在这段时期里，坐标系与解析几何并未出现.

17世纪解析几何出现之后，法国数学家洛必达抛弃了古希腊人的定义方法，将椭圆定义为在平面上到两定点距离之和等于常数的动点轨迹（也就是教材中的椭圆定义），并据此推导出了椭圆方程.

2.椭圆的标准方程中的隐性知识

教材中所给出的椭圆标准方程的推导是基于坐标系下的推导方法.而在对椭圆方程的探究过程中，许多数学爱好者给出了更为自然的推导方法，我们有必要对其进行了解.

（1）教材中椭圆标准方程的推导

根据椭圆的几何特征，类比利用圆的对称性建立圆的方程的过程.选择适当的坐标系，建立椭圆方程.

（2）椭圆方程推导中的隐性知识：椭圆发展过程中的四种推导方法

①余弦定理推导方法

如图6所示，设[PF2=z]，因为[PF1+PF2=2a]，所以[PF1=2a-z].

由余弦定理得[（2a-z）2=z2+4c2-4czcosθ=z2+4c2-4c（c-x）].

解得：[z=a2-cxa]

由勾股定理得[z2=a4-2a2cx+c2x2a2=y2+（c-x）2]

整理得[a2y2+b2x2=a2b2]即[x2a2+y2b2=1].

②利用椭圆第二定义进行推导——离心率

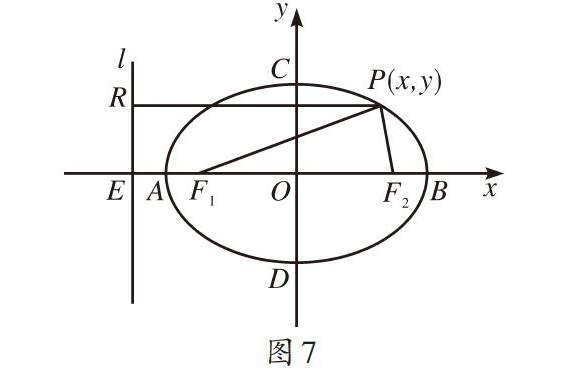
如图7所示，设[PF1PR=AF1AE=BF1BE=e]，[AB=2a]，[EO=ae]，[F1F2=2ae]，点[P（x，y）]的坐标满足[PF12=e2PR2][（ae+x）2+y2=e2ae+x2]，整理得[x2a2+y2a2（1-e2）=1]，记[b2=a2（1-e2）]即得[x2a2+y2b2=1].

3.椭圆简单几何性质中的隐性知识

在这一块讲到椭圆的离心率——我们把椭圆的焦距与长轴长的比[ca]称为椭圆的离心率，用[e]表示时，结合探究旁白中“[ba]与[cb]的大小能刻画椭圆的扁平程度吗？为什么？”来思考为什么要用[e=ca]来表示椭圆的离心率.

对于这个问题，[ba]与[cb]的大小可以用来刻画椭圆的扁平程度，但相对于[ba]与[cb]来说，[ca]更具有优势.我们知道椭圆是平面内到两定点的距离值和为常数的点的轨迹.第二定义中涉及的参数是[a]和[c]，为了保持一致，用[ca]来表示椭圆的离心率.

另外，圆锥曲线的统一定义为：“到定点距离与到直线距离之比为常数”，而这个常数的值恰好是[ca]，所以用[ca]表示离心率更具有统一性.

4.教材例题中存在的隐性知识

在講述完本节课知识点后，教材中例5的设计隐含了椭圆的光学性质（是指由椭圆一焦点射出的光线经过椭圆内壁反射后，必经过另一焦点，其等价于：椭圆上任意点的切线与两焦半径所成夹角相同），例6隐含了椭圆的第二定义.教师在讲例题的过程中，可以结合例题，将题后所隐含的知识讲给学生听，为学生在接下来练习过程中思路的开拓奠定基础.

5.“椭圆”知识体系中隐含的数学思想方法

高水平教师在教学活动中往往会对教学内容进行“点睛”——结合教学内容体现相应的数学思想方法.在“椭圆”的教学过程中，体现了分类与整合思想、函数方程思想、数形结合思想以及转化思想.在教学过程中进行数学思想方法隐性知识的渗透，无疑可以帮助学生更好地掌握知识的本质，学好数学.

四、小结

综合来讲，从教材中发现数学隐性知识，以“数学文化”为载体对教材中的隐性知识进行挖掘，可以对教材中知识讲授的顺序做一个“发生过程”的补充，使知识看起来更为连贯，学生接受起来也没有那么生硬.高水平的教师，能够透过现象看到本质，在教授教材中显性知识的同时，能挖掘出其后的隐性知识.此时，教师的身上自然散发着一种独特的数学光华与气息，携自身的全部数学涵养融入教室，融入课堂，融入学生，学生由此汲取数学的丰富营养.[8]

[  参   考   文   献  ]

[1]  陈淑彬.隐性知识显性化在数学教学中的作用[J].科技信息，2009（21）：637.

[2]  高湘萍.隐性知识的获得及其显性化的心理途径[J].全球教育展望，2003（8）：27-29.

[3]  顾沛.数学文化[M].北京：高等教育出版社，2008.

[4]  王芳，汪晓勤.HPM视角下椭圆概念教学的意义[J].中学数学月刊，2012（4）：57-60.

[5]  邹佳晨. 椭圆的历史与教学[D].上海：华东师范大学，2010.

[6]  王海青，李晓波.从阿波罗尼斯到柯西：“圆锥曲线”研究方法的变迁[J].数学通报，2018（10）：26-31.

[7]  汪晓勤.椭圆方程之旅[J].数学通报，2013（4）：52-56.

[8]  李祎.高水平数学教学到底该教什么[J].数学教育学报，2014（6）：31-35.

（责任编辑 斯   陌）