一道北京大学夏令营试题的多种证法

陕西师范大学附属中学 (710061)

张锦川

试题在ΔABC中，求证：cosA+cosB+cosC>1.

本题是2017年北京大学夏令营考试的一道试题，题目短小精悍，立足高中基础知识，能很好地考查学生数学能力，是高校选拔优秀学生的良好素材.笔者经过思考，给出了以下几种证明方法.

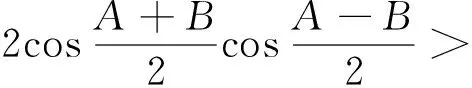
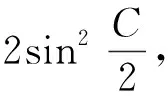
证法2:因为cosA+cosB+cosC=

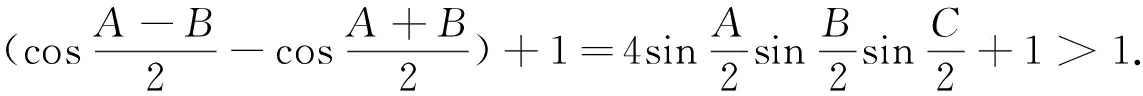
证法3:不妨设A≥B≥C，则B，C均为锐角.

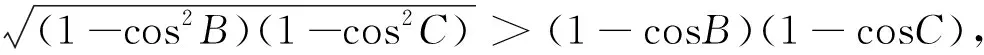
证法4:不妨设a=x+y，b=y+z，c=z+x，x,y,z∈R+.要证cosA+cosB+cosC>1，即证

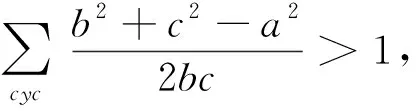
证法5:要证cosA+cosB+cosC>1，即证

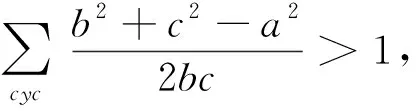
证法6:假设cosA+cosB+cosC≤1，则有acosA+acosB+acosC≤a，bcosA+bcosB+bcosC≤b，ccosA+ccosB+ccosC≤c，以上三式相加，得(acosB+bcosA)+(bcosC+ccosB)+(ccosA+acosC)+acosA+bcosB+ccosC≤a+b+c,即acosA+bcosB+ccosC≤0，即sinAcosA+sinBcosB+sinCcosC≤0，即sin2A+sin2B+sin2C≤0，即2sin(A+B)cos(A-B)+2sinCcosC≤0，即cos(A-B)-cos(A+B)≤0，即2sinAsinB≤0，得出矛盾，所以假设不成立，原不等式成立.

证法7:不妨设ΔABC的外接圆的直径长为1.

(1)若ΔABC为直角三角形，则cosA+cosB+cosC>1显然成立；

(2)若ΔABC为锐角三角形，如图1所示，则cosA+cosB+cosC=cos∠BDC+cos∠AEC+cos∠ADB=CD+AE+AD>CE=1；

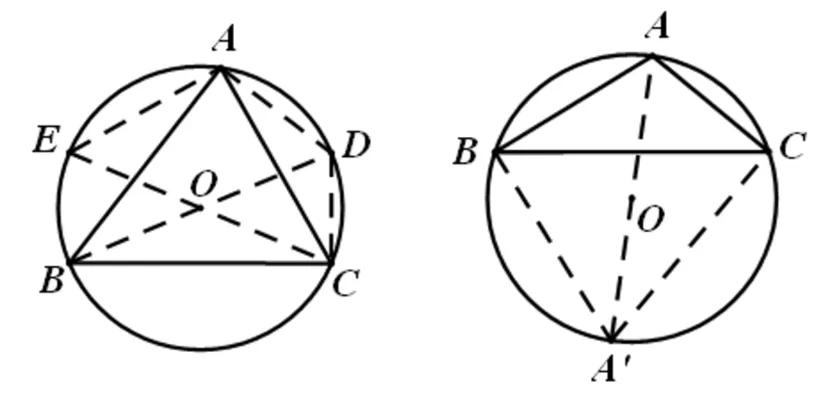
图1 图2

(3)若ΔABC为钝角三角形，不妨设角A为钝角.如图2所示，设∠BAA′=α，∠CAA′=β.则cosA+cosB+cosC=cos(α+β)+cosB+cosC=cosαcosβ-sinαsinβ+cosB+cosC=AB·AC-A′B·A′C+A′B+A′C=AB·AC-(1-A′B)(1-A′C)+1.因为AB>AA′-A′B=1-A′B，AC>AA′-A′C=1-A′C，所以AB·AC>(1-A′B)(1-A′C)，从而得出cosA+cosB+cosC>1.

综上所述，cosA+cosB+cosC>1.