一道解三角形问题的多角度思考*

江苏省海门中学 (226100)

李乃洋

解三角形问题是高中数学的基本题型，近年也出现了其与不等式相联系的综合问题.笔者最近在课上讲评一道解三角形求范围问题，针对学生的不同思考，略作整理，以探此类问题的不同角度认识.

题目已知ΔABC的三边a,b,c依次成等差数列，且a2+b2+c2=21，则b的取值范围是.

角度一：立足解三角形，利用正弦定理和余弦定理进行边角转化

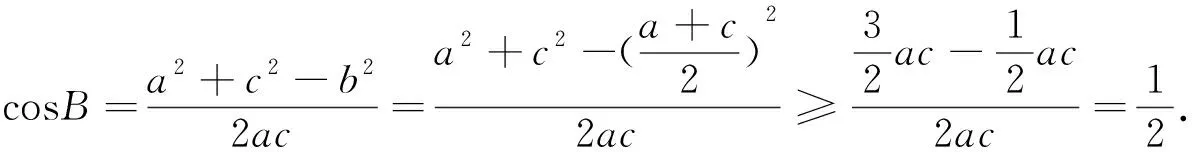
反思：解法1中利用了角B的范围(有界性)得到边的关系解不等式求得b范围，但也有学生指出如何确定cosB<1是否扩大了角B的范围从而影响计算结果.

角度二：利用等差数列构造消元

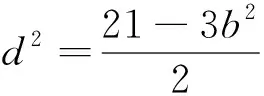
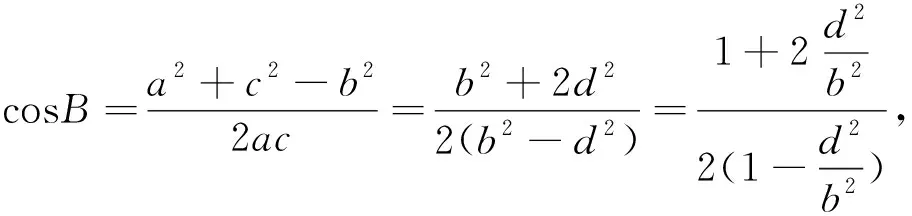
角度三：利用函数与方程思想转化为方程有解来计算

反思：方法3很好的体现了数学转化思想，将几何问题划归为代数(方程)问题，此方法可以理解为判别式法求解最值的延伸.

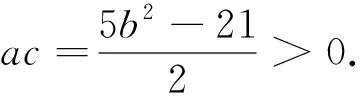
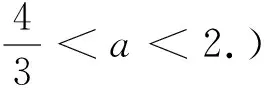
角度四:巧用均值不等式放缩

反思：利用不等式可以灵活产生不等关系，但是弊端是有时所求范围不精确，更多是借用不等式比较大小或研究最值问题.

角度五：基于曲线与方程转化为非线性规划问题

因为a+c=2b,a2+c2=21-b2，消去b得5a2+5c2+2ac=84(*)(含a,c乘积项)，所以联想此方程是某曲线的方程.

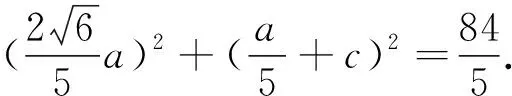
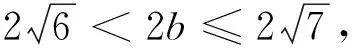
图1 图2

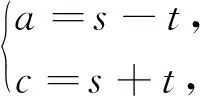
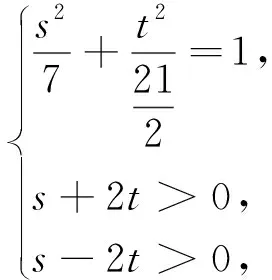
解法8：利用正交变换(旋转变换)不改变曲线图形特征来研究

角度六：对目标函数平方消元

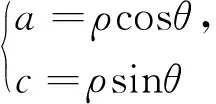
波利亚在其《怎样解题》中提到解题需要寻求有用的思路，“从不同的角度来考虑题目”，强调不同的细节，从不同的途径反复考查同一细节，以不同的方式进行组合，从不同的角度来利用它们.“你可以尝试寻找过去所获知识之间的联系”.试着想想过去类似情况下是什么帮助了你，试着在你考查过的过程中认出一些你熟悉的东西，试着在你认清的东西中发现一些有用的东西，这是对一个问题多角度认识的直观体现.