三大数学思想妙解三角题

福建省莆田第二中学 (351131)

蔡海涛

我们知道，三角函数是高中数学的重要模块，也是每年高考必考的问题.教学中我们发现，有些学生解决不了一些并不复杂甚至是简单的三角问题，认真分析其原因，基本上是因为这些学生无法在思想的高度上来引领方法，或是因为思想方法不明确而导致不懂得如何来解题.所以，笔者从思想方法的角度来谈谈三角解题的些许感悟，与各位同仁分享，不当之处请多指正.

一、函数与方程思想

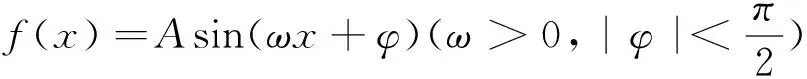
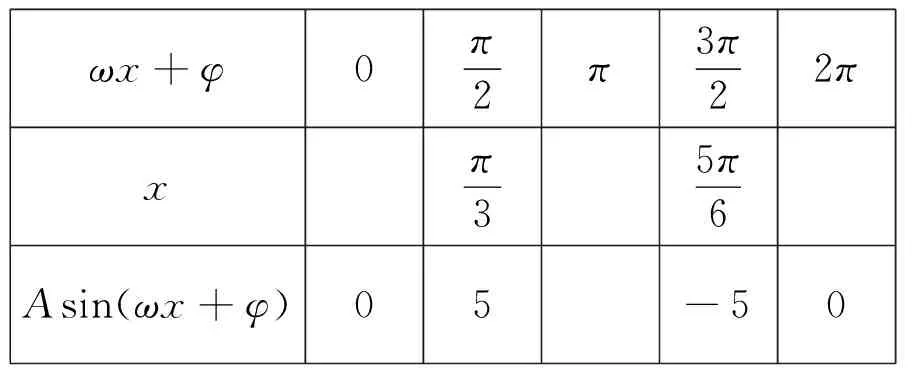
ωx+φ0π2π3π22πxπ35π6Asin(ωx+φ)05-50

(Ⅰ)请将上表数据补充完整，填写在答题卡上相应位置，并直接写出函数f(x)的解析式；

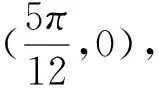
分析：第(Ⅰ)步中补充数据的难点在第一行数据的填写，很多学生的思路是从用“五点法”画函数图像这个角度来考虑，先利用周期性求ω的值，再确定φ的值.其实本题也可以利用函数与方程的思想，利用已知条件求解含ω和φ的方程组来处理.

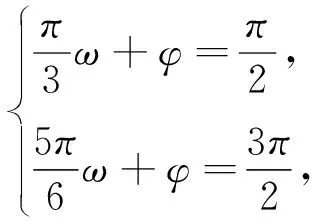
评析：方程思想是从问题的数量关系入手，运用数学语言将问题中的条件转化为方程，然后通过研究方程使问题获解，第(Ⅰ)步的关键是确定ω和φ的值，可以利用方程的思想来处理.

例2 已知函数y=sinx+2cosx在x=θ取得最大值，则tanθ=.

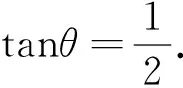
评析：三角函数是初等函数的一种，因此它具有函数的一般性质和解题规律，对于函数单调性问题的处理，导数是个有力的工具.

二、整体思想

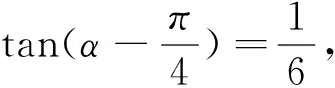
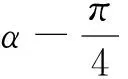
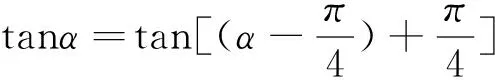
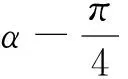
在讲解例3后，教师提出如下问题：

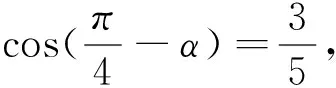
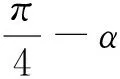
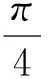
评析：为了更好地运用整体思想，换元是条不错的途径，可以把已知角“强行”化为单角，更清楚地发现待求角与已知角的关系.在给值求值,通过寻找待求角与已知角关系的问题均可用这种方法进行求解.整体思想在三角函数中的应用是十分广泛的，研究形如函数y=Asin(ωx+φ)的图像与性质时，亦可用整体思想，把ωx+φ看做一个整体来进行处理.

三、化归与转化思想

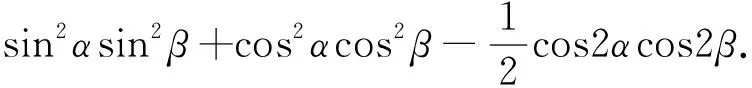
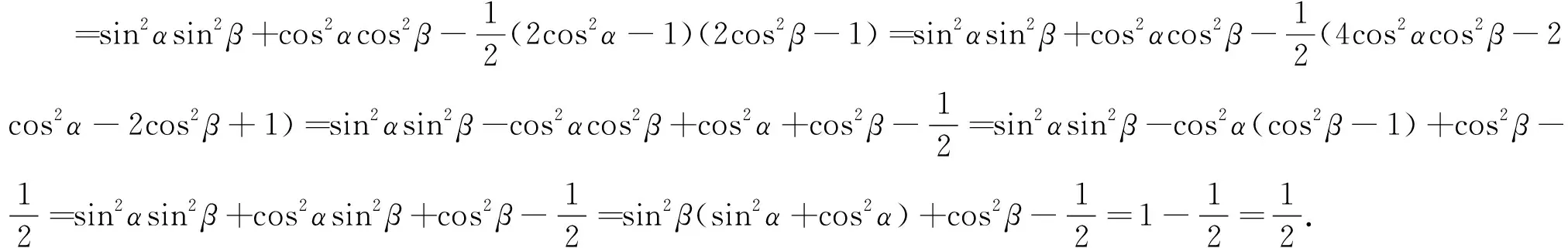
评析：方法1转化的思路是从“角”入手，把复角2α、2β转化为单角α、β，然后再进行化简；方法2转化的思路是从“名”入手，第一步把cosα化为sinα，从而使得前两项含角α的三角函数同名，达到化简的目的；方法3转化的思路是从“幂”入手，化二次为一次，从而得到化简；方法4转化的思路是从“形”入手，先对二次项进行配方，使得结构形式比较简洁，得到化简的入手途径.

由于三角公式多，方法灵活多变，很多学生对一些三角恒等变换问题往往不知从何入手.化归与转化的思想是在研究和解决数学问题时借助数学知识和数学方法，将问题进行转化，使抽象问题具体化，复杂问题简单化，未知问题已知化，进而达到解决数学问题的目的.所以，让学生掌握化归与转化思想，遵循一些规则，就不难解决问题了.事实上，从“角”、“名”、“幂”、“形”四种方向入手就是对三角恒等变换，化简求值常用的转化手段.