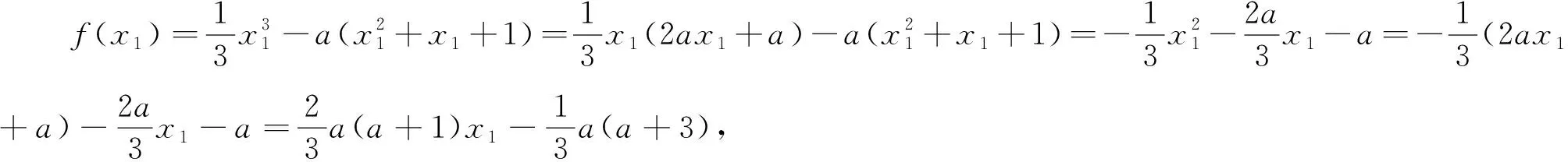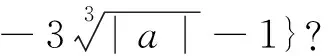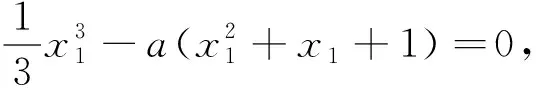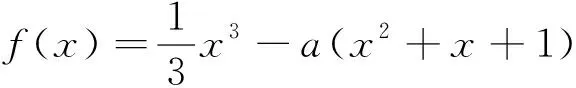高考导数压轴题的那“点”事

广东省广州市真光中学 (510380)

黄林盛

核心素养下的高考对学生的综合素养的提出了新要求，函数零点问题是高中数学考察学生综合素养的很好途径，主要体现在基本初等函数的图像，渗透着转化、化归、数形结合、函数与方程等思想方法，在培养思维的灵活性、创造性等方面起到了积极的作用.近几年的数学高考中频频出现函数零点存在的问题，其形式逐渐多样化，难点在于函数零点所在区间内的取点问题.本文将以两道高考题以例，阐述函数零点所在区间内应如何取点的基本方法.

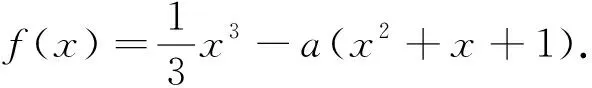
(1)若a=3，求f(x)的单调区间；

(2)证明：f(x)只有一个零点.

解：(1)略；

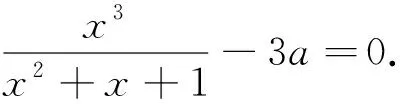
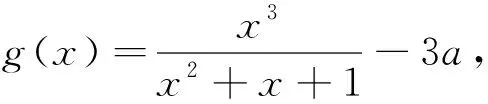
综上，f(x)只有一个零点．

评析：如何思考到取3a-1,3a+1？

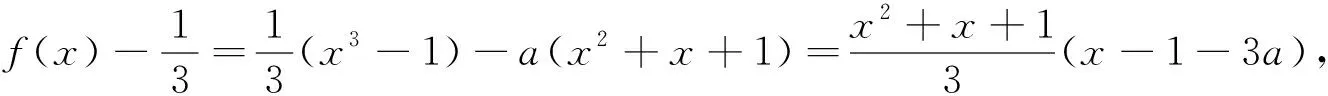
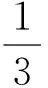
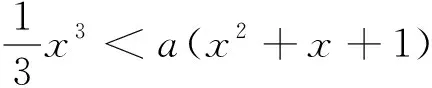
方法二：f′(x)=x2-a(2x+1)=x2-2ax-a,

①当△=4a2+4a≤0即-1≤a≤0时，f′(x)≥0恒成立，且等号仅在a=-1或0，且x=a时取得，所以f(x)在R上单调递增.

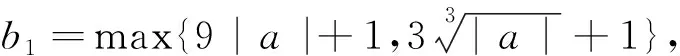
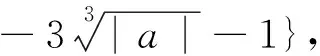
②当△=4a2+4a≥0即a<-1或a>0时，x2-2ax-a=0有两个不等实根，不妨设为x1,x2(x1

综上所述，f(x)只有一个零点.

评析:如何取得零点区间为(-3|m|-1,|m|+1)呢？

思路2：由g(t)=t3+t2+t-m可得，试点，g(0)=-m，g(-1)=1-m，g(1)=3-m，g(m)=m3+m2=m2(m+1),g(2m)=8m3+4m2+m=m(8m2+4m+1)，g(-m)=-m3+m2-2m=

-m(m2-m+2),g(-2m)=-8m3+4m2-3m=

-m(8m2-4m+3)，因为8m2+4m+1>0，m2-m+2>0，8m2-4m+3>0都恒成立，即有

g(2m)g(-m)<0,g(2m)g(-2m)<0.

试题呈现2 (2015年高考全国Ⅰ卷文科数学第21题)设函数f(x)=e2x-alnx.

(1)讨论f(x)的导函数f′(x)的零点的个数;

当a≤0时，f′(x)>0，f′(x)没有零点；

通过以上探究过程，可以总结零点区间端点选取的一般步骤：

步骤1：先分析当x→∞或x→a时，f(x)的符号，确定影响符号的关键项，然后通过等价转化使得y=f(x)各项均为基本初等函数;

步骤2：由于放缩的需要，有时候需适当缩小零点区间端点所在区间，一般说来，若区间为(a,+∞)(a<0)或(-∞,a)(a>0)型，通常取(0,+∞))或(-∞,0)型，对于区间为(a,b)，型，区间通常可取(a,b′)，ab′>0型;

步骤3：一般来说，在不影响决定函数符号的前提下，常常要用到不等式或转化成求某个函数在区间上的最值问题进行放缩，最终得到一个含参的可解不等式即可解出区间端点.

常用的放缩公式：

第一组：对数放缩

(放缩成一次函数)lnx≤x-1，lnx

第二组：指数放缩

(放缩成一次函数)ex≥x+1，ex>x，ex≥ex;

第三组：指对放缩

ex-lnx≥(x+1)-(x-1)=2.

第四组：三角函数放缩

第五组：以直线y=x-1为切线的函数