对2018全国卷几道高考导数试题的另解及思考

四川省南充高级中学 (637000)

张小丹

一 试题及解析

例1 (2018全国卷Ⅲ理科数学21题)已知函数f(x)=(2+x+ax2)ln(1+x)-2x.

(1)若a=0，证明：当-10时，f(x)>0；

(2)若x=0是f(x)的极大值点，求a.

1.对比答案

官方参考答案

解：(ⅰ)若a≥0，由(1)知，当x>0时，f(x)≥(2+x)ln(1+x)-2x>0=f(0)，这与x=0是f(x)的极大值点矛盾；

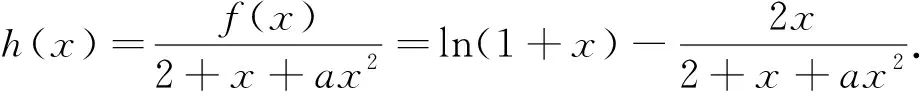
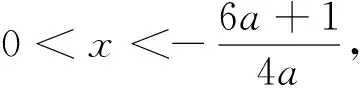
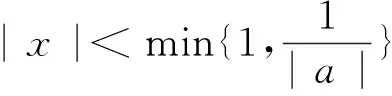
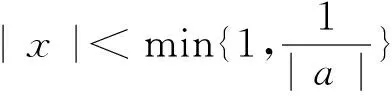
③如果6a+1=0，h′(x)=

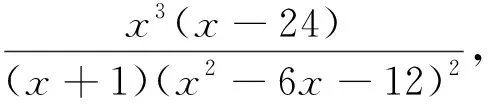
端点分析法答案

解：f(0)=0，∵x=0是f(x)的极大值点，∴在x=0的附近(除x=0)有f(x)<0(*)

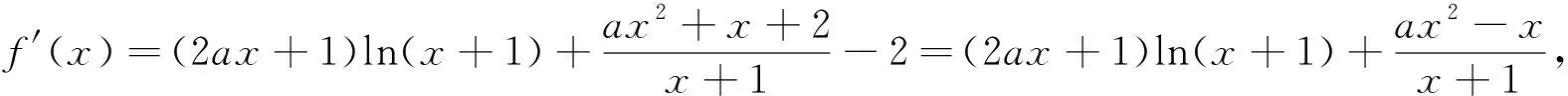
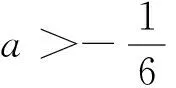
∵函数f″(x)在(0，+∝)上连续，∴∃x0>0,使得当00，∴f″(x)在(0,x0)上单增，∴当x∈(0,x0)时，f″(x)>f(0)=0，∴f′(x)在(0,x0)上单增，∴当x∈(0,x0)时，f′(x)>f′(0)=0，∴f(x)在(0,x0)上单增，∴当x∈(0,x0)时，f(x)>f(0)=0，这与(*)式矛盾；

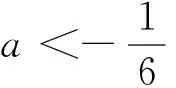
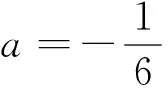
又f′(0)=0，∴当-10，当x>0时，f′(x)<0，∴f(x)在(-1,0)上单增，在(0,+∝)上单减，∴x=0是f(x)的极大值点.

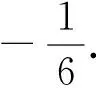
2.反思感悟

对于参考答案，个人认为“构造函数h(x)，并分析它与f(x)的关系”是一个难点，该难点恐怕很多学生，甚至老师都不易想到.所以，就解题思路而言，参考答案确实需要较强数学直觉以及解题功底.

对于端点分析法，想到它的突破口是题目的设问方式(可转化为一个恒成立问题)及隐含条件f(0)=0，这是导数中运用“端点分析法”(解决一类恒成立问题的方法)的必要条件.若注意到此，那么接下来就是运用“端点分析法”求解了.

个人认为“端点分析法”目标明确，思路流畅，与参考答案相比，有其独到的优势.

实际上，在今年的高考试题中，还有两道导数试题也可用此法.

例2 (2018全国卷Ⅰ文科数学21题)已知函数f(x)=aex-lnx-1.

(1)设x=2是f(x)的极值点，求a，并求f(x)的单调区间；

官方参考答案

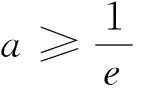
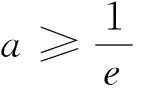
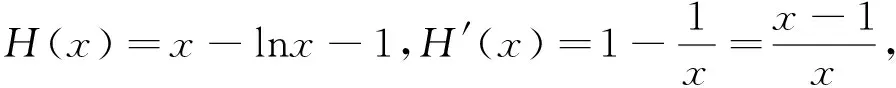
端点分析法答案

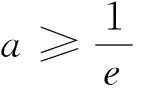
又g′(1)=0，∴当01时，g′(x)>0.

∴g(x)在(0,1)上单减，在(1,+∝)上单增.∴g(x)≥g(1)=0.于是f(x)≥g(x)≥0.从而原命题得证.

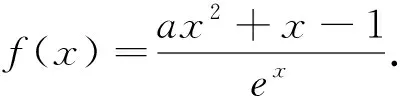
(1)求曲线y=f(x)在点(0,-1)处的切线方程；

(2)证明：当a≥1时，f(x)+e≥0.

官方参考答案

解(2):由题意,原不等式等价于ex+1+ax2+x-1≥0恒成立.

令g(x)=ex+1+ax2+x-1，∴g′(x)=ex+1+2ax+1，g″(x)=ex+1+2a，∵a≥1，∴g″(x)>0恒成立，∴g′(x)在(-∝,+∝)上递增，∴g′(x)在(-∝,+∝)上存在唯一x0使g′(x0)=0，∴ex0+1+2ax0+1=0，即ex0+1=-2ax0-1，且g(x)在(-∝,x0)上单减，在(x0,+∝)上递增，∴g(x)≥g(x0).

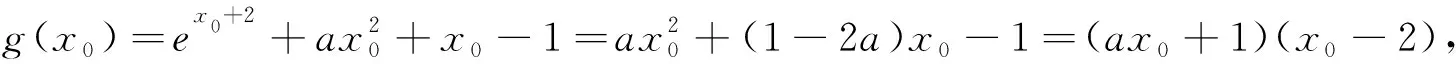
MOOCs是一种新型开放式的网络课程，它是由诸多愿意分享及协作以便增强知识传播的学习者所组织发布的，传播于网络上的大规模课程，具有以下几个特点：

综上所述，当a≥1时，f(x)+e≥0.

端点分析法答案

解(2)：不等式f(x)+e≥0等价于ax2+x-1+ex+1≥0，设g(x)=ax2+x-1+ex+1，当a≥1时，g(x)=ax2+x-1+ex+1≥x2+x-1+ex+1，设h(x)=x2+x-1+ex+1，∴h′(x)=2x+1+ex+1，易知h′(x)在(-∝,+∝)上递增，又h′(-1)=0，∴当x<-1时，h′(x)<0，h(x)递减，当x>-1时，h′(x)>0，h(x)递增.

∴h(x)≥h(-1)=0，于是g(x)=ax2+x-1+ex+1≥x2+x-1+ex+1得证，从而原不等式得证.

二、方法总结

端点分析法是解决导数中一类恒成立问题的常用方法.此类问题特征较为明显，一般是具有“对任意x>a(x≥a)，不等式f(x)>0(f(x)≥0)恒成立”(**)这样的形式或者可以化为这样的形式，且满足f(a)=0(f′(a)=0或f″(a)=0)，即代入区间端点，刚好可使不等式取等号.

具体解题思路如下：

③证明当f′(a)<0时不满足题设(必要性)；

④证明当f′(a)≥0时满足题设(充分性).

说明：(1)若f′(a)=0，则证明f″(a)<0(f″(a)≥0)不满足(满足)题设；

(2)并非所有满足条件(**)的题目均可用端点分析法，即有时必要性满足，但充分性不满足.具体问题需要具体分析.

三、其他试题

在近几年的高考试题中，类似试题并不少见.

题1 (2017全国卷Ⅱ文科数学21题)设函数f(x)=(1-x2)ex.

(1)讨论f(x)的单调性；

(2)当x≥0时，f(x)≤ax+1，求a的取值范围.

题2 (2016全国卷Ⅱ文科数学20题)已知函数f(x)=(x+1)lnx-a(x-1).

(1)当a=4时，求曲线y=f(x)在(1,f(1))处的切线方程；

(2)若当x∈(1,+∝)时，f(x)>0，求a的取值范围.

题3 (2016四川卷理科数学21)设函数f(x)=ax2-a-lnx,其中a∈R.

(1)讨论f(x)的单调性；

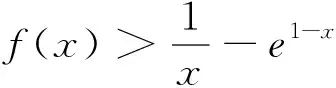
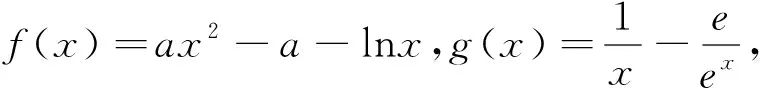
(1)讨论f(x)的单调性；

(2)证明：当x>1时，g(x)>0；

(3)确定a的所有可能取值，使得f(x)>g(x)在区间(1,+∝)内恒成立.