基于数学素养视角 深度挖掘数学本质——“多边形内角和”教学例谈

江苏南京市溧水区教育局教研室 吴义明

江苏南京市溧水区实验小学 徐菊花

【缘起】

《多边形内角和》是苏教版小学教材四年级下册第七单元的内容，是在学生认识了“三角形、四边形和梯形”以及掌握了三角形内角和是180°的基础上来进行教学的。这一内容是苏教版独有的“特色”单元“探索规律”中呈现的，其他版本小学教材大多未涉及此内容。苏教版教材是将这一内容作为小学中“图形与几何”与中学几何知识教学的一次衔接。苏教版教材编写用意很明确：一是作为学生“探索规律”的素材；二是通过学生的观察、操作、归纳等具体的活动，发现多边形内角和的计算方法，培养学生动手操作能力和发展学生的空间观念，为中学几何知识学习作铺垫；三是培养学生的好奇心，感受数学活动的挑战性。笔者多次听这一节公开课，困惑很多，首先困惑的是为什么这一节课会成为公开课的“宠儿”，是本身的内容有价值魅力，还是能体现数学的特点，或者是因为学生容易掌握，便于践行当下新课程理念？笔者至今也没弄清楚，搞明白。笔者还困惑在为什么苏教版教材把这一内容放到小学四年级来教学，笔者认为中学只要几分钟就能搞清楚的，在小学四年级来教，教师要花一节课，费九牛二虎之力，有的学生还没完全掌握，其意义又何在，作用又有多大呢！公开课上教师大多想渗透三个方面的主要目标：一是多边形的内角和可以根据三角形的内角和推算出来；二是从简单问题想起，有序思考是探索规律的有效方法；三是可以把新问题转化成能够解决的问题。这样的课堂看上去符合新课程标准倡导的动手实践、自主探索、合作交流这样的理念，但笔者总感觉到这样的数学课缺点什么。形式的东西多，实质性的少。笔者深深感到当下《多边形内角和》一课的教学未能从数学素养视角出发，缺乏数学味，不能深度挖掘数学的本质，没有把学生的好奇心通过这一内容激发出来，也没有看到学生课堂上表现出对数学知识挑战的欲望，与苏教版教材编者意图是否完全吻合，值得我们推敲。为了不让疑惑飘忽而过，笔者做了一份调查：某县城实验小学四年级全班52名学生，在已经学习了“三角形内角和是180°”这一内容的基础上，设计了一份《多边形内角和》一课的自学单。

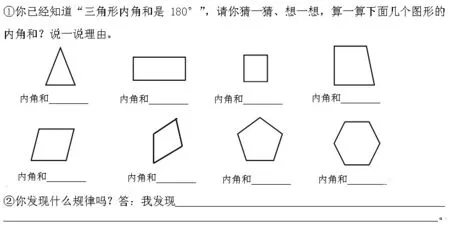
《多边形内角和》自学单

调查结果：

第一题，47名学生都能填写正确，三角形180°，四边形360°，五边形540°，六边形720°，只有3名学生在五边形和六边形两道题上出了差错，另有2名学生在四边形这道题上出了差错，但教师稍加点拨，他们也就豁然开朗了。

第二题，有一半以上的学生能表达出：只要将多边形分成三角形，就能推出内角和。还有学生用公式（n-2）×180°表示结果。

调查结果让笔者非常诧异，这一内容对学生并不是想象中的那么难，公开课中需要费神费力地去研究吗？笔者进一步了解发现，该班学生有的已经看了教材了；有的已经与家长、同学交流了；有的在培训班里已经提前学过了；还有少数学生的学习力较强，稍加思考也就解决了。原因是这部分内容学生是有基础的，在推导三角形内角和是180°时，很多方法已经渗透了。

如①折纸法

（有平角是180°可推导出三角形内角和是180°）

②划分法

（长方形、正方形四个直角和是360°，一个直角三角形的内角和是360°÷2＝180°）

有这样一些方法的铺垫，“多边形内角和”只要将多边形分成若干三角形，得出内角和就不是难事了，原因就在此。

教师可以尝试让学生探讨四边形的内角和，学生的方法很多。

生1：我用量角器分别量了一下4个角的度数，加起来就能知道和是360°。

师：用量的方法准确吗？

生1：不知道。但正方形和长方形是准确的，一定是360°。

生2：我把四个角撕下来拼到一起，发现刚好拼成一个周角，我确认四边形内角和是360°。

生3：我只要加一条辅助线把四边形分成两个三角形，再用180°×2就得出这个四边形的内角和是360°。

生4：由此类推，五边形加两条辅助线，把五边形分成三个三角形，五边形的内角和是180°×3＝540°；六边形加三条辅助线，把六边形分成四个三角形，六边形的内角和是180°×4＝720°。因此，多边形内角和的度数，只要将它分成若干个三角形，就能知道多边形内角和的度数。

其中，一名学生问了一个看起来“怪”的问题，让很多教师都大跌眼镜，傻了眼。生问:（n-2）×180°这一公式中，n是多边形边数，180°是一个三角形的内角和的度数，而减2这里的“2”表示什么？为什么要减去2，而不是减3、减4……呢？笔者带着这一问题问过多位小学数学教师，也请教过中学数学教师，答案均不能让人满意。这一看起来“怪”的问题一直困扰着笔者！基于以上困惑，笔者产生了如下深度思考：

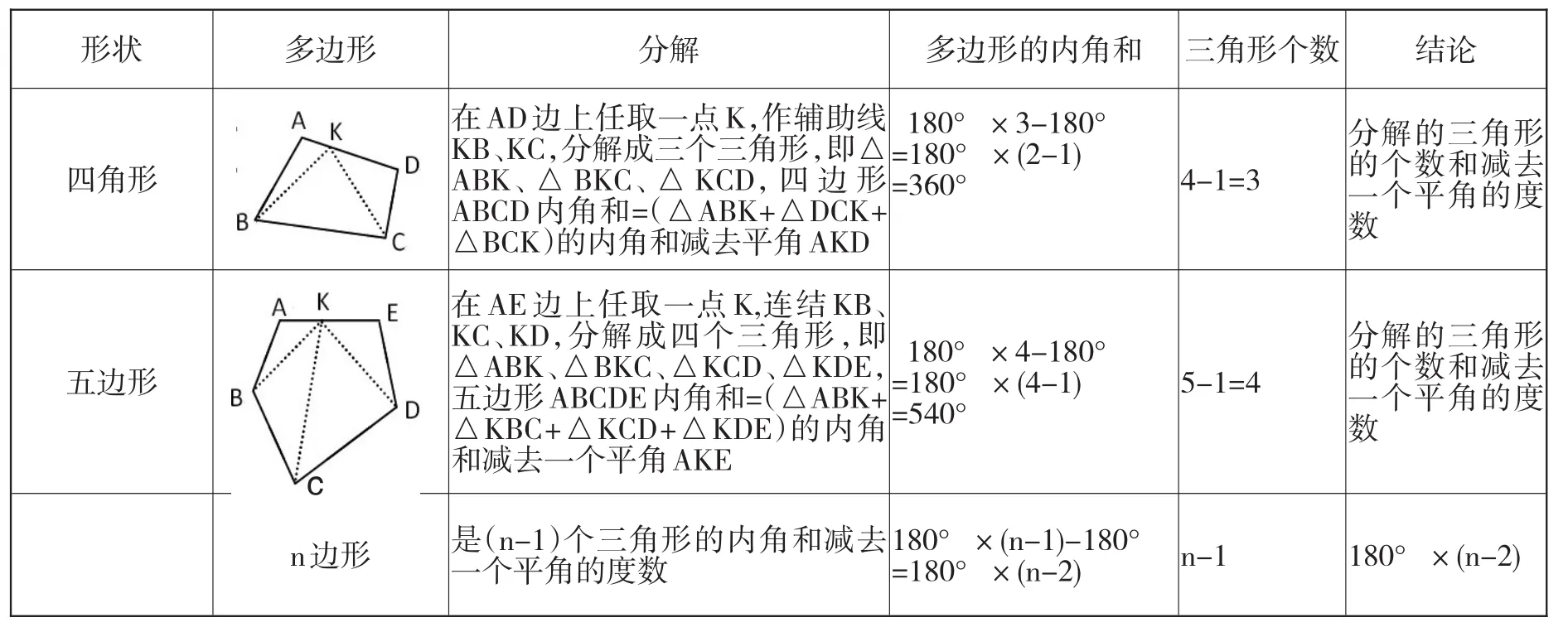
【深度思考一】根据三角形内角和是180°，通过找规律可以推算出多边形内角和的计算公式：多边形内角和=（n-2）×180°。这里的180°是一个三角形的内角和，n为多边形的边数，公式里的减2,2是什么意思？为什么减2，而不是减1减3呢？这一问题有挑战性，有思维的深度。最简单的回答是：多边形的边数与三角形个数的关系是相差2,但为什么相差2呢？深层次的原因在哪里呢？究其原因，分析如下表

这样学生就不会对公式中为什么减2产生疑问，确实是多边形的边数与三角形个数的关系是相差2，相差2的原因也就能搞清楚，弄明白，学生不仅知其然，而且知其所以然。

【深度思考二】以上两种教法是从教材视角来教，是不是还有不一样的教法呢？

【深度思考三】从多边形的任一边上的任一点出发，分成若干个三角形，推导出多边形的内角和。

【深度思维四】从多边形内任意一点0将多边形分解成若干个三角形，推导出多边形的内角和。

综上所述，教材所给的教例，仅是一种教学方式，从数学理性精神角度去思考，为什么是n-2，这里的“2”是怎么回事？追根溯源就产生了从新的教学角度来推导180°×（n-2）这一公式，如果学生在学习中能够充分感悟到数学的理性精神，就能体会到理性精神的价值，这样学生的思维品质就会得到提升，学生思维的深刻性、灵活性、敏捷性、批判性、创造性就得到了培养，进而学生能产生对数学的好奇心、积极探索数学领域奥秘的愿望，这才真正说明学生的数学素养得到了升华。

《多边形内角和》这一内容到底如何来教学呢？笔者认为：基于教材的逻辑视角，基于数学素养的视角，即用数学的眼光观察，用数学的思维分析，用数学的语言表达。用数学的眼光就是强调数学的抽象，用数学的思维分析就是强调逻辑推理，用数学的语言表达就是强调数学模型。从更为简明的角度，我们应把理性的思维置于数学素养的核心，将数学思维的学习与具体知识内容有机结合，用思维方法的分析去带动具体知识内容的学习。这样教学不仅能深度挖掘数学的本质，而且能使这节平淡的课变得回味无穷、妙趣横生，同时还能把数学的感觉交给学生，使数学具有数学味，最后达到从数学材料中抽取其直观意义的高层次思维，这是数学学习所追求的一种境界。♪

【深度思考一】

?

【深度思考二】

?

【深度思考三】

?

【深度思考四】

?