基于学生立场 让学习真发生

江苏南京致远外国语小学 范韦莉

数学学习是学生自我感知、自我体验、自我建构、自我内化的过程，在这一过程中他们习得知识，学会思考，积累数学活动经验，感悟数学思想方法，形成数学素养。可见，如果试图引起、维持和促进学生的学，教师必须基于学生立场遵循“学”的规律进行教学设计。本文拟从剖析当下课堂中存在的某些现象入手，结合具体内容的教学，谈谈如何通过顺应学生达到自主建构，从而促进学习在课堂中真正发生。

一、立足学生经验生发研究问题，提供充沛自由的思维空间

每个学生都有各自的生活经验和知识基础，面对需要解决的问题，他们都是从自己特有的数学现实出发来构建知识的，这就决定了不同的学生在解决同一问题时会有不同的视角。有资料表明：经验、闲暇、自由是学生自主发展的三个重要条件。在数学课堂中，为学生提供安全、和谐、自由、闲适的环境更容易激发学生思维的敏感性，真正促进师生在课堂上实现有效对话与沟通。

【教学片段】苏教版数学六年级上册“分数乘整数”出示例题，学生得到算式×3并猜想结果为后，进入如下教学：

学生尝试后出示合作学习要求，教师让学生在小组里交流。

师：说一说每种方法是怎样计算的？

学生出现了如下四种方法（如下图）：

学生交流后，明确：（1）分数乘分数是后面的内容，我们不能用还没有学的知识来验证。（2）画图、写成连加算式、化成小数都可以验证出×3＝。

师：想一想哪些方法之间是有联系的？

重点引导学生沟通画图和加法算式间的联系：两种方法都可以看作是3个相加，画图可以一眼看出结果是，写成分数连加，计算时分母不变，分子相加，结合图来看，实际上就是3+3+3，也就是3×3。

师：无论是画图，还是写成分数连加，或者化成小数，都利用了转化的思想，把新知转化成旧知解决的。

师：你认为每种方法的优缺点是什么？

生：画图可以清楚直观地表示出结果，但是数据太大画图就很麻烦了。

有些分数不能化为有限小数，有一定的局限性。

写连加算式能帮助我们得到结果，但是数字太大写连加算式太累。

师：分母不变，分子是3个3连加，可以想成什么？（3×3）想成乘法是不是就可以不用写很长的加法算式了？比如，分子是100个3，这里就可以写成100×3。（根据学生回答，相机板书：

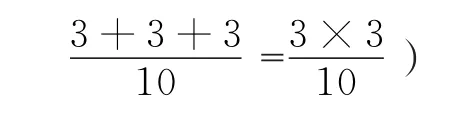
师：其实，老师写的这些都是头脑里想的过程，只不过你们没有写出来罢了。

对于新知的探究，要顺应学生的学习心理，体现自主、合作、开放，本环节中，教师设计了三个层层递进的交流话题，面对这样熟悉而又有挑战的数学问题，学生有着自己朴素的理解经验，虽然表达的方法、呈现形式各不相同，但这些经验都是丰富而珍贵的。上述教学中，教师脱离程式化的教学，给学生足够的时间和空间去探究，激起学生内心深处学习、求知、探索的欲望，同时在教师的点拨下将算理和算法融为一体，促进学生的学习真正发生。

二、倾听学生对话领悟知识本质，提供个性自由的表达空间

现代教学论指出：教学实则是师生、生生、生本之间进行一种多元有效的对话，每个学生不同形式的表达恰恰是他们各自主体发展判断、选择、付诸行动的能力。教师倾听学生在课堂上的对话，是学生个体精神自由的体现，通过富有个性的对话，为学生自主表达思想、自由发展能力提供沃土。

【教学片段】苏教版数学四年级下册“三角形的高”

师：你们刚才提到了高度，三角形的高到底指的是什么呢？（学生跃跃欲试举手）别急，这两个三角形已经印在了学习单上，把你心中的高用线表示出来。

（汇报交流）

生1：我把右边的边描了一下（如图1），它们能代表这两个三角形的高，这条边的长度越长，它就越高。

图1

生2：我不同意。老师，我可以上来画一画吗？

这名学生自信地在黑板上画出这样两个图形（如图2）。

图2

生2：你们看，很明显第二个三角形右边的长度比第一个长，但却是第一个三角形更高啊！

师：（问生1）你接受他的建议吗？

第一位同学害羞地点点头。

师：还有别的画法吗？

生3：老师，我是这样画的（如图3）。我从做最上面一个点往下面作了一条垂线，这两条垂线可以代表三角形的高。

图3

师：我明白了，你是从最上面的顶点出发，到底边作了一条垂直线段对吗？是这样画的举个手。教师环视了教室，发现大部分学生都是这样画的。

生4：我有补充，我和他的画法一样，但我多了一个直角符号。

师：怎么想到加直角符号的？

生4：我们曾经画过点到直线的距离，当时画的就是垂直线段，是要加直角符号的。

师：看来你们对三角形的高已经有了自己的感觉，确实，我们可以从最上面这个顶点出发（指着学生的作品），到它对面的这条边，也就是它的对边，作一条垂直线段表示出三角形的高。

教师应该是一个倾听者，倾听学生最本质的想法，捕捉学生想法中有价值的内容。上述学生在建立高的正确表象的过程中，学生的思维在碰撞，在辨析，在交流，在提升，对高的正确表象的建立也是主动的、逐步完善的，对高的内涵的理解也逐步加深，整个过程中知识的生长是自然的，学生的数学理解以及思维能力也得到了自然生长。

三、指引学生回顾提炼思想方法，提供个体自主的反思空间

美国心理学家波斯纳提出：没有反思的经验是狭隘的经验，最多只能是肤浅的知识。因此在教学中，教师要组织学生进行有效的回顾与反思，将学习过程中的学习活动变为思考的对象，进行反省。学习者自我反思的过程是梳理知识系统的过程，是自我对过去所积淀的经历、思想的反思性理解。

1.回顾探索过程，总结探索经验

例如，在学习“解决问题的策略（列表）”后，教师及时引导学生回顾整理：“我们是怎样研究列表策略的？为什么要学习列表的策略？这个新策略对我们以后有什么新的价值？”这样的过程既着眼于学习内容的思维化，又着手于反思性思维训练，以实现学习逻辑向认知逻辑的转化，有效实现了学生经验系统化、结构化的完整历程。

2.激发新的探索，引发更多有意义的思考

人类对于未知数的探索是无止境的，课的结尾不应该让学生的数学思考画上句号，而是要努力激发新的思考，引发新的探究欲望，鼓励学生真正走向主动探索、自主发现、自主发展之路。如在回顾“表面涂色的正方体”的探索活动之后，教师可以鼓励学生课后进一步探索“表面涂色的长方体”，每一类涂色小正方体的个数又会隐含哪些有趣的规律。

3.反思探索策略，感悟数学思想方法

自主建构过程中经常会自觉或不自觉地应用一些数学思想方法，组织回顾与反思时要重点引导学生结合探索的过程，感悟由特殊到一般、由具体到抽象的归纳思想，以及其他一些有助于学生提高探究学习能力的研究方法，如认真观察、分类比较、画图思考、灵活转化等。

可以预见，未来的课堂教学，无论是在教育观念上，还是在实践方式上，都将朝着“以学生的学习为中心”这一核心目标转型，也就是基于“顺应学生，以学定教”的理念努力地接近学生的思维原点。因为我们知道，只有顺应了学生，才能真正找到意义建构的最佳路径，学生的学习才能真正发生。♪