让学习“真”的发生——例谈“数形结合”的深度学习

江苏常州市新北区奔牛实验小学 陈 莉

受应试教育和班级授课制的影响，大部分教师轻过程，重结论。学生在这种教学模式的影响下，就会懒于动脑，机械接受，但是浮于表面的模仿毕竟经不起时间的考验，时间一长，付之东流，稍有变式，全盘崩溃！如何让学习真正发生？笔者认为，采用数形结合的方法，深入浅出地展示知识形成的过程和原理，能帮助学生追根溯源，触及思维的深处，让数学学习有深度。

数形结合是指通过简单的图形、符号和文字所作的示意图等，促进学生形象思维和抽象思维的协调发展，沟通数学知识间的联系。所谓数学深度学习，是指数学学习不是仅仅得到一个结论，而是以培养学生的思维方式为主导，关注学生的思维训练与提升，要深入研究数学知识的内在联系，揭示规律的形成过程，提炼蕴含的数学思想，体验数学的理性精神，从而培养学生深层次思考和学习的能力。

一 数形结合明晰算理

相关研究表明，算法是自动化的，即使在不知道其背后原理的情况下，仍可以经过反复操练掌握和使用算法，这样教学学生俨然成了一名操作工，机械、呆板，如何让学生在计算课的教学中思维活起来，笔者结合案例谈一谈自己的做法：

例如：苏教版数学三年级上册《笔算两、三位数除以一位数》第一课时。

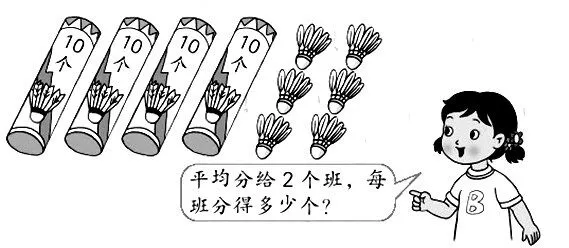
分析：学生已经学习了表内除法的竖式计算，学生对除法竖式的雏形有一定的认识，但是今天的内容与已有经验相比，无论是方法、算理、过程，都有很大的跨度，如何让学生在计算课上学得有滋有味，我采用了层层递进的教学方式。

摆一摆：（1）46÷2等于多少呢？请小朋友拿出小棒摆一摆，分一分，看看得数是多少？谁愿意来演示一下你是怎么分小棒算得数的？说说你是怎么分的？（4）我们分小棒时，一般分三步：先分整捆的，再分整根的，最后合起来。

想一想：（1）看着情境图，在脑子里分一分，看看得数是多少？（2）说说怎么分的？（先分整筒的，再分整个的，最后合起来）

算一算：还有同学是这样算的，40÷2=20，6÷2=3，20+3=23，你能看懂吗？

比一比：不管是摆小棒，还是分羽毛球，还是算式，都有什么共同特点？（都是分三步：第一步分大单位，第二步分小单位，第三步加起来）

教一教：46÷2也可以用竖式来计算，先算十位上4除以2商是2（即2捆小棒，2桶羽毛球，2个十），所以2要写在十位，再算个位上6除以2得3（也就是3根小棒，3个羽毛球，或3个一），因此3要写在个位，最后合起来商就是23。

本节课的重点是掌握笔算两位数除以一位数，但是笔者却在教学重点之前浓墨重彩，层层铺垫，先摆，再想，接着算，手、口、脑多种感官并用，饱满、丰实，最后通过比较得出不管是摆，还是分，还是口算，都是三步。在此基础上教学笔算两位数除以一位数，水到渠成，虽是轻描淡写，却突破了难点，尤其是摆、分、算之间三步曲的沟通，有效实现了算法和算理的内在统一，学生不仅学得轻松，而且明白了算法中的原理。

二、数形结合辨析概念

小学生的思维以具体形象为主，到高年级才初步出现形象思维到抽象思维的过渡。因此，以形象思维为主的小学生学习抽象的数学概念有一定的难度，化解这一矛盾的重要工具就是“数形结合”，通过“数”与“形”的有效结合，使抽象的概念找到直观的支撑模型，从而使复杂的数学问题变得简明、形象，帮助学生更好地理解数学。

例如：苏教版数学五年级下册《认识假分数》练一练

分析：这一题，是把一个长方形看作单位1，虽然教师反复强调，但是学生还是会把正确答案想成，究其原因，还是没有真正理解“单位1”，针对这种情况，我采用了以下教学策略：

（4）小青吃完自己的一部分，感觉还没有吃饱，又把小红吃剩的一块吃了+，请问小青这时吃了这块饼的几分之几？（1或）

“单位1”的教学是分数教学中的一大难点，教师苦口婆心，反复强调，效果未必就好，但是如果能依托学生已有的经验，从具体的事例出发，让学生形成表象，再建立抽象概念，学生对这一概念的印象一定是清晰的、深刻的，只有这样，思维才有触动，学习才真正发生，而不是浮于表面的模仿。

三、数形结合验证规律

小学阶段的规律教学一般采用归纳法，无非就是先举几个简单的例子，然后找一找有什么规律，再举一些更广泛意义的例子进行证明，从而得出规律，这样的教学虽然很适合小学生，但是毕竟不够严谨，因为举例毕竟有局限性，万一有漏网之鱼呢？如果采用数形结合的方法来验证规律的普适性，岂不更完美。

例如：苏教版数学五年级下册《和与积的奇偶性》

分析：和的奇偶性规律很简单，如果直接告诉学生规律，2秒钟学生就能做题，但是因为学生没有经历规律的探索过程，学生很容易遗忘，如何让课堂饱满，如何让学生的思维活起来，让数学学习有深度，我采用了以下教学方法。

（1）学生通过举例已经发现了“偶数+偶数=偶数、奇数+奇数=偶数 、奇数+偶数=奇数”这些规律。

（2）通过几个简单的例子就说明这个规律无懈可击，你们觉得靠谱吗？（不靠谱）可以再举一些数字大一点的例子。

（3）举例再多，但是万一有漏网之鱼呢？怎么办？怎么证明这个规律呢？

（4）出示小棒图。

偶数：111111……11

奇数：111111……111

你能根据图示说一说为什么“偶数+偶数=偶数，奇数+奇数=偶数，奇数+偶数=奇数”吗？

（5）因为偶数是2个一组，2个一组，没有多余，再加一个偶数，还是2个一组，2个一组，没有多余，合起来还是不会有多余，只是组数变多了，偶数变大了。如图：

偶数1：111111……11

偶数2:111111……11

（6）奇数加奇数也可以用图来表示。

奇数1：111111……111

奇数2：111111……111

你能圈一圈，表示出为什么“奇数+奇数=偶数”吗？（把余下的2根圈成一组）

（7）当然奇数加偶数也是同样的道理。

奇数1：111111……111

偶数2：111111……11

奇数加偶数的和2个一组，2个一组，还会有1根多余，所以和是奇数。

……

规律教学是小学数学教学的一部分，大部分教师只注重规律的总结以及规律的运用，而忽视了寻找规律的过程，以及规律背后的原理，这种浮于表面的规律学生短时间内容易记住，但是由于没有触及思维深处，容易被遗忘，并且不会灵活运用，学生的思维没有得到提升，运用数形结合的方法不仅能知其然，还能知其所以然。

著名数学家华罗庚曾经说过：“数缺形时少直观，形少数时难入微；数形结合百般好，割裂分家万事休。”在数学课上，采用数形结合的方法，让学生真正放飞思维，让数学课上得有内涵、有活力、有滋味、有实效、有后劲，这样的学习才是真正的学习，有深度的学习。