低结构教学高思维发展——《平行四边形与梯形练习》教学及思考

周珊珊

低结构化教学是一场教学观的变革。在此教学过程中，学生数学学习能力的提升、思维层次的提高，不仅仅是通过教师的精心预设、反复打磨和多次试教来实现，还应由学生自主发起，并于师生和谐的互动过程中满足学生的内在需要。低结构化课堂是一种在遵循数学知识内在的联结中引发深层次思维，促进全体学生自主全程参与，体验由浅入深、由外而内的学习方式。本文，笔者将以《平行四边形与梯形练习》一课为例，诠释低结构化教学如何激活高思维发展的课堂。

【教学过程】

●片断一：低情境导入，高空间发展。

课件依次出示：点 A、B、C、D，如图1。

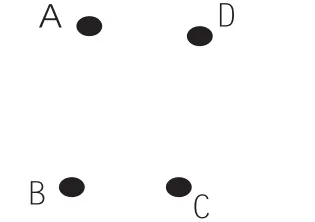
图1

师：把这四个点顺时针连起来，会是什么图形？

生：（异口同声）平行四边形。

师：都认为是平行四边形，对吗？

生：对。

出示：背景方格图。（如图2）

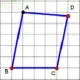
图2

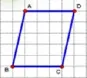
图3

师：怎么回事？怎样才能变成平行四边形？

生：把D点往上移。

师：随便移吗？

生：不能，要移到D点上面的方格交叉点上。（如图3）

师：为什么？

师：怎样的四边形是平行四边形？

生：两组对边分别平行的四边形。

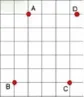
图4

图5 直角梯形

图6 等腰梯形

师：点A、B、C三点不动，如果点D往左平移并把四点依次连起来，会是什么图形？

生：梯形。（如图4）

师：为什么不是平行四边形了？

生：现在的四边形只有一组对边平行。

师：点D继续往左平移又会是什么图形？

生：直角梯形。（有两个角是直角，如图5）

师：点D再往左平移，现在会是什么图形？

生：等腰梯形。（如图6）

师：继续平移点D呢？

生：梯形……三角形。

师：点D再向左平移，是什么图形？

生：梯形。

（课件演示，如图7）

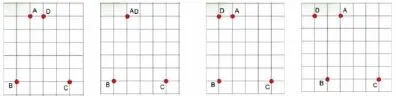
图7

师：这个点D一直往左平移，都是梯形吗？点D在这条线上平移的过程中，你有什么发现吗？

发现：AD和BC始终是互相平行的，当另一组边也互相平行时就是平行四边形，当另一组边不平行时就是梯形，A和D两个点重叠在一起时是三角形。在变化的过程中，它们的高始终不变。

【思考：“低结构”就是起点很低、很简单，表述直白不复杂。这节练习课的导入从最基本的点开始，把四点顺时针连接，致使学生共性认同，一致认为连成之后是平行四边形。教师借助方格图，引发原认知冲突，学生重新梳理、回顾平行四边形特征。这样低结构化的情境导入不仅有效沟通了平行四边形与梯形之间的关系，强化了平行四边形与梯形的特征，发展了学生的空间想象力，更让学生在变与不变中沟通图形之间的联系，引发“高发展”的巩固练习。华罗庚先生说：“善于‘退’，足够地‘退’，‘退’到最原始而不失去重要性的地方，是学好数学的一个诀窍。”这节课简单地导入，朴素的引导，给学生充分自主的想象，逐渐形成“思维激荡”。】

●片断二：低结构练习，高思维激发。

课件出示：在平行四边形中（如图8）添上一条线段，把它分割成两个完全相同的图形，你有几种不同的分法？

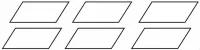
图8

师：读一读，这道题主要有几个要求？

生：两个要求：1.添一条线段；2.分割成两个完全相同的图形。

师：每位同学在练习纸上动手分一分，画一画。（学生自主练习，教师选取学生不同的作品在黑板上张贴出来，如图9）

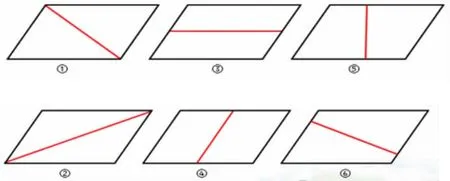
图9

师：你们的分法和这些同学一样吗？还有不同的分法吗？如果把这些画法进行分类，你会怎么分？

生：我认为分成两个完全相同的三角形、平行四边形、梯形三类。

师：一个平行四边形可以分成两个完全相同的三角形、平行四边形、梯形，反过来可以怎么说？

生：两个完全相同的三角形、平行四边形、梯形可以拼成一个平行四边形。

师：既然两个完全相同的图形可以拼成一个平行四边形，那么其中一块的大小与平行四边形有什么关系？

生：其中一块的大小都是原来平行四边形面积的一半。

师：同学们分割的过程中，分成两个什么图形最容易？

生：三角形。

师：为什么？其余两种呢？

生：要用尺量一下各自的长度，有点麻烦。

师：有没有可能不量，也像分割三角形一样随意画一条线就一定能分出两个完全相同的图形？（同桌讨论）

讨论后学生发言：先画出平行四边形的两组对角线，中间的交叉点就是这个平行四边形的中心点，我们只要过这个中心点随意画直线，就一定可以分出两个完全相同的图形。（如图10）

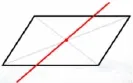
图10

【思考：这个环节教师准备了一道基本的、开放性的操作题。这道题的结构和要求简单，起点很低，但是思维空间却很大。教师留足了思考的空间和时间，让所有学生都可以提出自己的想法、建构自己所学。探究过程中，教师适度点拨，学生自己发现了知识的联结点，沟通了平面图形之间的关系，为今后三角形、梯形的面积教学做好了铺垫。低结构化教学，学生不再被动地接受知识，而是积极自主地参与学习，在不同的思维碰撞中理解、发现、体验和反思知识，实现对知识的再认识、再理解。】

●片断三：低要求预设，高拓展延伸。

师：四边形除了都有四条边，还都有四个角。研究了边，我们接下来研究角。（出示图11）大家算算这两个四边形它们的内角和各是多少度？

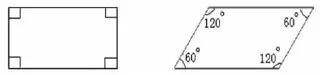
图11

师：我们在教材练习十一中通过测量知道四边形的内角和是360°。从内角我们会想到外角，你知道四边形的外角在哪里吗？（学生猜想并指出）

师：一般我们把每条边的延长线与另一条边组成的角看作外角。（课件逐次呈现长方形的外角，如图12）长方形的外角有几个？

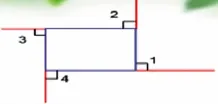
图12

生：四个内角对应就有四个外角。

师：它的外角和是多少？

生：90°×4=360°。

师：观察每个内角和外角之间有什么关系？

生：加起来是平角，是180°。

师：平行四边形它的四个外角在哪里？它们的和是多少呢？（小组探究）

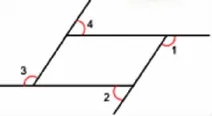
图13

学生汇报：平行四边形一个内角和一个外角的和是180°，这样的有四组。（如图13）用四组平角和减去平行四边形的内角和360°就是它的外角和了。算式是 180°×4-360°=360°。

师：那么这个梯形的外角和是多少呢？（如图14）

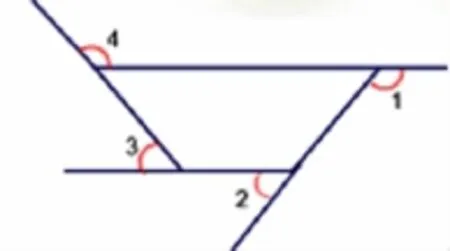
图14

生：和求平行四边形外角和思路一样，也是180°×4-360°=360°。

师：对四边形外角和你们有什么猜想？

生：四边形外角和有可能都是360°。

师：真的是这样吗？你们还联想到了什么？

生：可以用求四边形内角和与外角和的办法去计算五边形、六边形的内角和与外角和……

【思考：从边的研究想到角的研究，从内角和想到外角和，从四边形外角和想到多边形外角和，一步一步推想，看似结构简单，实则内涵丰富。学生不仅把之前的学习知识进行了有效沟通与联结，更激发了他们大胆的猜想，从而去预见更深层次的数学知识。这样低结构、开放式的教学，引领每一位学生去观察、去思考、去发现，学生与材料之间、学生和学生之间、学生与教师之间都产生了有效的思维互动，实现了课堂思维拓展的最大化，学生在学习中真正成为课堂的主人。】

【课后思考】

一、“整体把握，注重思维”的练习设计

张奠宙教授指出：“数学教学需要从整体上把握，要让学生能发散的思考。”本节练习课从基础的“点”引入，连点成线，连线成面，进行不同形体特征的巩固。在“点”的平移与构成的“面”的交替变化中，打通平行四边形、梯形、三角形内在的纵横关系，活化了学生的元认知结构；接着安排一道基础的开放性操作题，通过动手画、合作讲，发现知识的连接点，激发学生创新思维；最后从研究图形的“边”转向研究图形的“角”，从不同的视角去理解和把握平行四边形与梯形的整体内容，让学生的学习视野更广阔，激发学生的思维与灵感。本课的设计与教学，教师立足高远，总揽全局，鼓励数学想象，伴以实际操作，诱发发散思维，做到了“既见树木又见森林”。

二、“知识迁移，关注经验”的生长省悟

学生建构系统的数学知识，绝不可能是一个教师简单告诉的过程。教师要根据学生已有的知识生长点和现有的学习状态，让学生经历一种经验性的活动，鼓励学生跳出已有框架，去重新发现并建构自己的知识网络。具体地，在平行四边形与梯形的基本特征巩固中，学生运用已有经验判断平行四边形，导致集体性错误，激发学生学习的内驱力。造成认知冲突后，教师巧借方格图，让学生从数学概念的角度去判断，点D不断平移，从平行四边形引出一般梯形、直角梯形、等腰梯形，再经一般梯形、三角形、一般梯形，回归到平行四边形、梯形……这个环节通过课件显性的刺激、教师语言的引导以及学生合理的想象，深入理解图形特征，极好地沟通了图形之间的关系。到片断三，学习从“边”的练习引到“角”的研究，以教材习题内角和的知识为已有经验引发学生对外角和的探索，学生的思维再一次被点燃……直至生长到课外。这样的设计照顾了不同学生的学习需求，诱发了发散性思维，让学生对平行四边形和梯形的认识不再是单一的、独立的，而是整体的、生动的。

低结构化课堂需要教师积极转变教学观念，放下权威，留足学生学的空间；更需要教师深入把握数学知识本质特征和学生能力起点，统揽全局、高屋建瓴，设置门槛低、思维深、有空间的问题和环节。我们需不断实践，让学生在动态、交互、思维激荡的低结构高挑战课堂中学会学习、学会思考、发展思维，培养其创造与创新能力，更好地实现数学学科的育人功能。