挖掘数学本质提高数学素养——《平均数》教学

金朦朦 叶仙花

【教学内容】

浙教版五年级上册第42～44页。

【教学过程】

一、创设情境，激趣引入

师：这是六（1）班代表和六（2）班代表在投篮比赛中的成绩。哪个班投篮水平高？为什么？

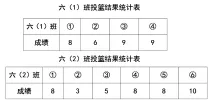
生：六（1）班投篮水平高，因为平均数高。

生：总成绩是六（2）班的水平高，但人数不一样，不能这样比较。

师：能具体说说吗？

生：如果人数相等，可以比较总数，人数不相等时不能比总数。

师：人数不一样的时候我们可以采用求平均数来解决问题的方法。

【设计意图：教师借鉴教材设计，用“人数不等”的情境，引起求取平均数的需要。这里，学生对“平均数”的理解尚混同于“平均”的数，“平均”的数既是教学要借力的基础，也是教学应提升的地方。】

二、理解平均数的意义与计算方法

1.认识平均数。

（1）平均数算法的理解。

师：什么是平均数？

生：总和÷人数=平均数。

师：把所有成绩合并起来，即总数，再平均分，也就是假定每个人一样多，这个看起来一样多的数就叫平均数。平均数这个统计量可以较好地代表整体水平。

师：六（1）班平均数是多少？

生：（8+6+9+9）÷4=8（分）。

（2）平均数“虚拟性”的理解。

师：六（1）班平均数“8分”刚好等于①号同学的成绩“8分”。这两个“8分”表示的意思一样吗？

生：不一样。①号同学是真的投了8分，平均数是刚巧等于8分，是把大家的分数匀一匀的结果。

师：平均数“8分”代表的是六（1）班的整体水平，而①号的“8分”是这位同学的个人水平。

【设计意图：从算法角度初步理解平均数，结合图像，引导学生从“平均分”过渡到“匀一匀”。体会平均数与实际收集到的数据有不同，平均分是对整组数据分析的结果。】

2.理解平均数。

（1）平均数意义的渗透——“移多补少”。

师：观察六（1）班的条形统计图，老师把平均数表示出来了，你发现了什么？

生：从③号、④号的9分中各拿出1分给②号，就是平均数8。

生：比平均数多出的部分和比平均数少掉的部分一样多。

师：把四个数据中比较大的一些数分一部分给小的数，得到的就是平均数。这其实是我们学过的“移多补少”，同样也可以使数据变得一样多，找到平均数。

（2）平均数意义的剖析——“变数游戏”。

师：如果将其中一个数变一变，平均数会发生变化吗？我们来玩一个“变数游戏”。

一变：②号由6分变为10分

生：②号拿出1分给①号，平均数是9，变大了。

师：平均数有没有可能变成10？为什么？

生：不可能，因为其他数都比10少，最高的10要分给其他较少的。

师：移多补少，平均数肯定比最高分低。

二变：②号由6分变为2分

生：平均数变小了。

师：有没有可能变小到2？为什么？

生：其他的数都比2大，移多补少，2要变大。

师：所以平均数肯定比最低分高。

师：从②号数值的变化，你有什么想说的？

生：平均数不可能是最低分，也不可能是最高分。

生：平均数肯定在最高分和最低分之间。

生：一个数变小了，平均数跟着变小；一个数变大了，平均数也跟着变大。

师：看来一组数据中任意一个变化对平均数都有影响。

三变：增加一组数据⑤，1分

生：增加了⑤号，是1分，平均数变小了。

师：为什么增加一个数，平均数反而变小了？如果⑤号是2分、3分呢？至少是几分，平均数才不会下降？

生：增加的数小于平均数，平均数变小；增加的数等于平均数，平均数不变；增加的数大于平均数，平均数变大。

师：请快速判断六（2）班的平均数可能会是几？

六（2）班的平均数可能是：

A.10分 B.3分 C.7分 D.6分

师：为什么不选A、B？平均数到底是多少呢？

生：（5+3+8+8+8+10）÷6=7（分）。

师：所以六（1）班的整体水平用8分表示，六（2）班的整体水平用7分表示，六（1）班投篮水平比六（2）班要高一些。

【设计意图：结合图示，开展“变数游戏”，通过猜想、验证，体会数据的变化对平均数的影响，感知平均数的多项性质，包括平均数与极值的关系、大于平均数的部分与小于平均数的部分之间的关系，以及新增数据和平均数的关系等，突破本节课教学的重难点。】

3．感受极值的影响。

师：六（2）班一位同学投了最高分10分，为什么平均数反而会更低呢？

生：因为②号才3分，拉低了平均数。

三、应用拓展

师：根据两个班投篮的整体水平，快速判断并说明理由。

（1）六（1）班③号的投篮水平一定比六（2）班⑤号的投篮水平高。（错）

（2）总体上说,六（1）班比六（2）班投篮水平高一点。（对）

（3） 六（2）班有一位同学的投篮水平是10分（10=7+3），那么，班里一定有一位同学的投篮水平是4分（4=7-3）。（错）

【设计意图：基于投篮情境，进一步提出问题，引导学生体会平均数的统计意义，强调平均数代表的是整体水平，不是个体水平。所谓的移多补少也不是个别的移多补少，而是“高于平均数的部分的和=低于平均数的部分的和”。】

四、综合运用

1．跳绳测试。

四位同学参加跳绳比赛，平均每人跳了128个，其中强强跳了150个，聪聪跳了130个，佳佳跳了129个。

师：迪迪跳得比平均数多还是少？为什么？

生：少，其他人都比平均数多，多出的部分都要给迪迪才能使迪迪变到平均水平。

师：如果佳佳只跳了120个，迪迪跳的比平均数多还是少？估算迪迪跳的个数。

生：比平均数少！强强比平均数多22个，聪聪比平均数多2个，佳佳比平均数少8个，还是多出的多，迪迪肯定比平均数少。

师：迪迪跳了多少个？

生：128×4-150-130-120=112（个）。

生：移多补少法：（150-128）+（130-128）=24 （个），24-（128-120）=16（个），128-16=112（个）。

2．达人秀歌咏比赛。

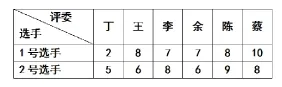
师：谁是冠军？求总数和求平均数，都可以？

生：总数算出来都是42分，平均数都是7分，分不出高低啊！

师：真的吗？你觉得从分数看，谁唱得更好些？

生：可能2号吧。1号选手的争议很大，评委中最低只给了2分，最高10分。

生：可是1号选手除了最低的2分，其余评委给的都比较高。

师：现实生活中为了打分更合理，总要分别去掉一个最高分和一个最低分，你见到过吗？现在算算看，谁在比赛中胜出？

3．立定跳远比赛。

生：去掉最高分，去掉最低分，得到最后的成绩一样。

生：计算平均分，聪聪获胜。

师：参加过跳远比赛的同学来说说，谁会获胜？

生：跳远取最高分。

师：实际生活中，立定跳远比赛是记最高成绩的，不算平均数。所以，看到一组数据，不能全用平均数来表示，而是要根据实际情况灵活选择！

【设计意图：进一步联系生活实际，促进对平均数的理解。既强调平均数的一些特性，也体会平均数的一些局限性，以及与需要解决的问题之间的实际匹配度。培养学生思维的深刻性与批判性及应用意识。】

【点评】

随着课程研究的深入，平均数教学从传统的侧重于对算法的识记和应用，逐渐演变为对“平均数是一种统计量”的本质的理解。

教师在情境和问题的设计上能够紧紧扣住平均数的本质，颇见功底。

投篮情境引入，由于人数不同，简单地联想到求取平均的数，带出平均数的算法；继而讨论“平均数8分”与“实际得8分”的差别，引导学生体会此统计分析的“平均”（学生所谓“匀一匀”）不能简单等同于先前除法计算的“平均分”，还另有一重“整体”水平的意义。

创设“变数”游戏，进一步体会组内数据对于平均数的影响，感知统计意义的平均数的各种性质，如介于极值之间，“多出的数=缺少的数”等等；问题有正有逆，均指向意义的理解。

进而，根据平均数推断个体和整体情况，有效地澄清了一些误解、偏见，而在思辨、澄清的过程中，又更加了解平均数与个别数据及数据整体之间的关系。

练习是三个校园生活中非常熟悉的比赛情境。跳绳比赛从算法上是已知平均数，逆向计算个别数据，但教师增加估计平均数的问题后，立即指向了意义的理解，也直接催生了两种不同的解法；歌咏比赛，体会平均数的局限性及为克服这些局限常用的一些补充手段；跳远比赛突破思维定势，先结合实际，想到取最高值，又返回数据，体会平均数对不同特点的数据组的适用性和说明性。这些练习篇幅短小，而内涵丰富，值得借鉴。