“系列课”背景下起始教材的比较研究与教学建议
——以《近似数与估算》教学为例
何月丰
数学知识是螺旋上升发展的。在上升发展的过程中,知识的外在形态会发生一定的变化,但还是在原来的知识链上。在一条链上的知识,会有几个关键的节点。从教学的角度看,这些节点就形成了一节节的数学课。因为这些课是由同一个起源发展而成,并在一条知识链上,就形成了一个“课系”,不妨称为“系列课”。
如果这样的理解是正确的,那么可以说明一个事实:没有一个数学知识是一节课能教完的,即所有的数学课都是系列课。
不同课系以及一个课系中的不同课,会受到不同程度的关注。例如《长方形的面积》,这节课备受关注,是研究热点,也就在一定程度上体现了我们对这节课是非常重视的,就把它单独拿出来研究了。换一个角度,《长方形的面积》其实是“面积计算”这个系列的一节课而已。
基于以上对“系列课”的认识,对《近似数与估算》的教材比较研究,除了整体上的横向、纵向等维度之外,还可从特有的“系列结构”、“系列起点”、“系列阶段终点”三个方面进行。下面笔者就“系列起点”——《近似数与估算》起始教材的比较研究,与老师们做一个交流。
所谓“起始教材”,即在整个“课系”中知识第一次正式出现时的教材。为了增强对比性,使研究更有宽度和深度,我选择了国内的人教版、浙教版以及美国的加州版三个版本教材进行比较研究。为了增强可比性,使研究更为细化,我拟定了教材立意、素材选择、特色方法三个比较点。
一、对三个版本《近似数与估算》起始教材的独立分析
1.对人教版《近似数与估算》起始教材的独立分析。
人教版(2012版)教材,《近似数与估算》第一次正式作为一个知识点进行教学,是在二年级下册第91页,该内容隶属于《万以内数的认识》单元。
教材立意:该起始教材的例题是教学将9985看成10000,所以教材立意为近似数的教学。同时在教学逐步推进的过程中,明确提出了“近似数”、“准确数”这样的术语,并给出了近似数的优点——更容易记住。
素材选择:在素材方面,教材选用了一个常见的生活情境,电视节目中主持人报了运动员人数为9985人,看电视的爸爸将人数说成“将近10000人”。然后通过“画外音”对话的形式,对两种说法进行对比,给出两种说法的特点。应该说,这样的素材选择,还是很有“生活气息”的。
特色方法:人教版此处教材的编排,“数直线”的使用可理解为是其特色之处。通过数直线,可使二年级的学生直观地看到9985与10000的“接近”,从而能更好地理解将9985看成10000的合理性。
2.对浙教版《近似数与估算》起始教材的独立分析。
浙教版(2012版)教材,《近似数与估算》第一次正式作为一个知识点进行教学,是在二年级下册第96页,是一个独立的单元。
教材立意:该教材的立意,从单元题目就可以看出来是估算。不过,仔细分析教材会发现,这里除了教学估算,还教学近似数,如估算时要把389看成400,其实就是近似数教学,把近似数作为一种估算的需要来处理,这种需要源于例题问题中的“大约”。
素材选择:在素材方面,浙教版选用了一个学生比较熟悉的生活情境——图书馆藏书情况,并以此为背景,转化成一个典型的加法问题,由此通过问题中的“大约”引出“估算”。以生活问题为背景,再转化成数学问题,本身就是浙教版教材的编排特色。
特色方法:浙教版这样的编排,把近似数与估算融合在一起教学,在此,且把这样的编排作为它的特色之处吧。另外值得一提的是,浙教版在第一次教学《估算与近似数时》就引入了“≈”。
3.对美国加州版《近似数与估算》起始教材的独立分析。
加州版教材,《近似数与估算》第一次正式作为一个知识点进行教学,是在一年级(加州教材不分上下册)的第251页(如下图),该内容隶属于第8单元(一年级一共14个单元)《100内数的认识》。

教材立意:该教材中标题“Estimating with Groups of Ten”的意思为“以10个为一组估计”,教材立意清晰可见——估计。从教材中我们也可以看到“以10个为一组”的估计行为——教材用不同颜色的小立方体表示,小朋友正在10个一组圈一圈进行数数。对于估计结果,教材采用选择性的方法,给出了30和50两个选项,让学生操作之后思考,这一堆小立方体可以估计成30个还是50个。所以,从这个过程上去理解,加州版教材表面是在教“估计”,其实是近似数的教学。
素材选择:在素材上,教材没有选用生活问题,没有给出进行估计的需要和背景,而是直接指向于行为——以10个为一组进行估算。
特色方法:加州教材的特色之处,在于给出了具有动作行为的估计方法——以10个为一组。同时,对于估计结果的确定,是选择性的(下面的练习也是这样的形式)。这样的处理,对于刚刚接触估计的一年级学生而言是有好处的。
二、对三个版本《近似数与估算》起始教材的对比分析与思考
在以上独立分析的过程中,其实也默默进行着对三个版本教材的对比。这种对比,既有立足教材立意、素材选择和特色方法这三个方面的,也有在这三个方面之外的。对比发现,区别还是比较显著的。
1.对教材立意、素材选择和特色方法对比分析后的思考。
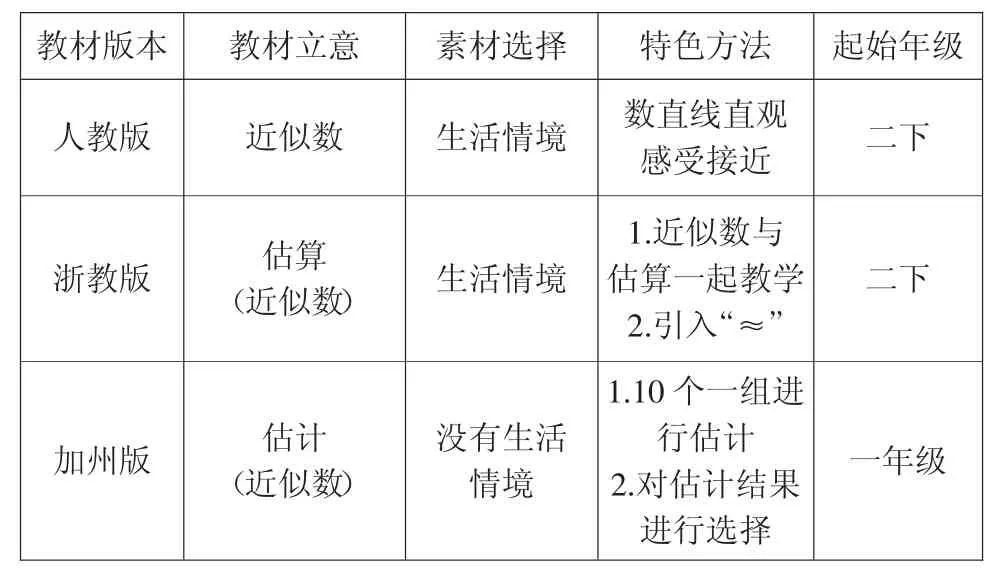
教材版本 教材立意 素材选择 特色方法 起始年级人教版 近似数 生活情境 数直线直观感受接近 二下浙教版 估算(近似数) 生活情境1.近似数与估算一起教学2.引入“≈”二下加州版 估计(近似数)没有生活情境1.10个一组进行估计2.对估计结果进行选择一年级
(1)通过对“教材立意”的对比分析可以看出,教学一旦牵涉到估算(估计),就会涉及到近似数的教学,而近似数可以独立教学。在这个问题上,我想也是好理解的,因为要估算(估计),就说明不需要一个准确的结果,这就自然地产生了近似数。例如浙教版教材要求两类书的总量,只要“大约”即可,加州版教材估计小立方体的数量,是要看实际数量更接近30还是50。这样,在计算两类书的总量时,用到了近似数,选择30或50也是近似数。
(2)通过对“素材选择”的对比分析可以看出,就比较的三个版本教材而言,国内和国外是有区别的。国内的教材都选用了生活情境,而国外是没有的。当然,国外这里只选用了一个版本的教材,不能以一概全。但就“生活情境”而言,我个人认为还是需要的。1980年美国数学教师联合会在《行动的纲领》这份文件中,第一次提出“把估计能力作为一种重要的数学素养”,并在后续的研究中形成了一定的共识,“必须让学生理解估计的意义,什么情况下的估计是合适的……”显然,生活情境的介入,对学生理解估计的意义,认识到什么情况下使用估计是非常有帮助的,由此能让学生深刻认识到“课本中的数学与现实生活中数学的联系”。
(3)通过对“特色方法”的对比分析可以看出,在起始教学近似数或估算时,“取整”是一个共同选择。人教版把9985看成10000,浙教版把389和308看成400和300,加州版将一堆小立方体估计成30或50。三个版本教材不约而同地用整十、整百、整千、整万作为学生首次接触近似数的“近似对象”,我想这是易于一二年级的学生理解和接受的。尤其是人教版和浙教版,都采用了更能体现“接近”的数据,就更加有利于学生的理解和接受了。
2.对三个版本近似数形成过程的分析与思考。
在对以上三个方面进行分析与思考的过程中,我注意到三个版本教材在作为结果的“近似数”的形成过程上有所区别,具体如下表。
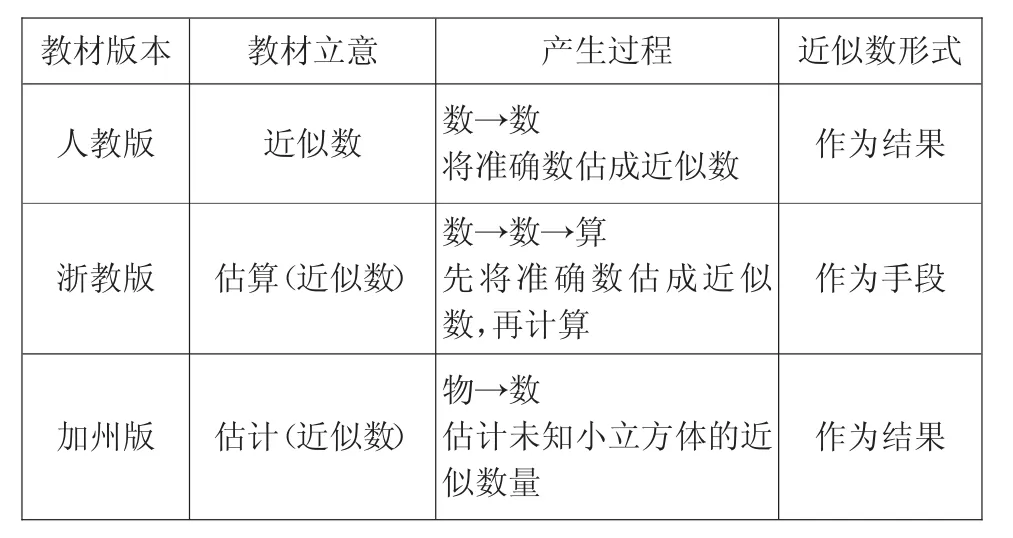
教材版本 教材立意 产生过程 近似数形式人教版 近似数 数→数将准确数估成近似数 作为结果浙教版 估算(近似数)数→数→算先将准确数估成近似数,再计算作为手段加州版 估计(近似数)物→数估计未知小立方体的近似数量作为结果
在“产生过程”上,三个版本的教材各不相同。
人教版教材是先给出一个准确数(运动员人数),再根据准确数得到近似数,采用了“数→数”的形式,近似数是作为结果来呈现的。
浙教版教材,先根据准确数(数的数量)得到近似数,再运用近似数进行计算,采用了“数→数→算”的形式,近似数作为一种计算手段参与。
加州版的教材,先是呈现一堆未知数量的小立方体,“数”是未知的,然后以10个为一组进行估计,近似数是作为结果来呈现的。这里需要思考的是,具体教材如何展开,即以10个为一组进行估计时,是否把具体数量数出来(如教材中是39),如果是数出来的,那么加州版教材采用了“物→数→数”的形式;如果没有数出来,那是采用了“物→数”的形式,显然这样的形式对学生的思维要求是比较高的。从标题“以10个为一组估计”理解,要充分发挥“10”的作用,因此我暂且把教材解读为“物→数”的形式吧。
通过上述分析和对比不难发现,相对而言,人教版的编排较为“单纯”,难度较低。
3.基于以上分析后的感想。
通过上述对于三个版本《近似数与估算》起始教材的比较,我最大的感觉是“这水有点混”。三个版本的起始教材,各有自己的立足点,在立意上区别明显,进而引发的就是课系的统一性不强。例如浙教版,起始教材就涉及到估算、近似数和“≈”,而人教版、加州版没有涉及那么多,那么这两个版本的教材必然要在后续的教学中去涉及这些知识,这就会造成课系发展不够统一,知识螺旋上升的趋势会不明显。这一点,与其他一些课的区别还是有较为明显的地方。
三、基于《近似数与估算》起始教材分析的教学建议
作为系列课的起始教材,关键在于“始”,即要做好启蒙教育工作,这样,才能更好地让知识生长。就《近似数与估算》而言,如何做好启蒙教育工作呢?基于对以上三个版本教材的分析及思考,我认为以下几点值得关注:
1.用“近似数”作为启蒙,使学生易于理解和掌握。
估算离不开近似数,但近似数可以独立教学。因此,在“近似数与估算”这个课系中,将近似数作为启蒙教学较为合适(如人教版)。一方面,这样的教与学更为“单纯”,不必考虑“算”,降低了难度,易于学生理解和掌握;另一方面,这也符合学生数学学习的一般规律,先认“数”(近似数),再学“算”(估算)。
2.以生活情境为载体,使学生感受到近似数的价值。
数学向来被看作是“一门与人类思想中的精确部分相一致的学科”(爱因斯坦)。学生在一二年级的学习中,接触的“数”和“算”,基本是“精确”的。现在要从“精确”转向“近似”,需要有一定的“价值取向”来支撑。这种“价值取向”,体现在教学中就是要让学生感受到产生并运用近似数的好处,显然,生活情境是一个很好的载体。通过生活情境,使学生感受到生活中运用近似数的情况,进而感受到近似数的价值。
3.以“取整”为近似方法,并借助数直线感受接近。
求得一个数的近似数,一般采用四舍五入或取整,其本质都是“接近”。相对而言,四舍五入的思维层次更高一些。因此,作为近似数的启蒙教学,以“取整”为近似方法,是一个好的选择。同时,为了使学生能更好地理解“接近”这个本质,建议借助数直线使学生能直观感知。在产生过程上,建议采用“数(准确数)→数(近似数)”的形式,在数据的选择上,要采用更能体现“接近”的数据,如人教版的9985→10000。

