对“矩形的性质”教学的思考

梅山堂

[摘 要] 从生长数学的角度来看，“矩形的性质”一课生长路径明显，笔者通过类比平行四边形研究的基本套路，引导学生进行矩形的相关研究，在研究矩形的过程中，进一步体会和巩固了研究几何图形的“基本套路”.

[关键词] 矩形性质；生长数学；基本套路；教学思考

2017年底，笔者有幸在蚌埠新城实验学校举办的“联动教研 分享智慧”教研活动中，与实验中学的孟婧文老师共同就沪科版数学八年级下册“19.3.1 矩形的性质”一课进行同课异构展示. 从生长数学的角度来看，矩形一课生长路径明显，学生在此之前已经具备了研究平行四边形的经验，而本节课的学习将是后面继续学习菱形、正方形性质的重要前提. 所以，笔者通过类比平行四边形研究的基本套路，进行矩形图形研究. 让学生在研究矩形的过程中，进一步体会和巩固研究几何图形的“基本套路”. 本文拟对本节课探究过程中的部分片段进行回放，并给出解读与思考，与各位同行研讨. 不当之处，欢迎斧正！

片段回放

片段1：情境创设

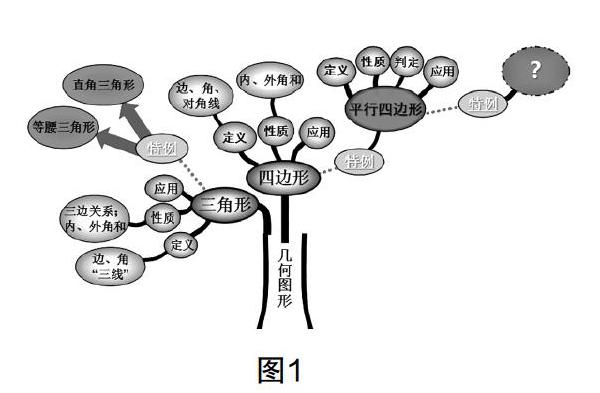
师：（展示如图1所示的知识生长树）回忆三角形和平行四边形的学习过程，我们是通过怎样的顺序来研究的？学生回答后，师生共同梳理平行四边形的研究过程. （定义-性质-判定-应用）

师：如果今天这节课，我们继续针对平行四边形深入研究下去，会研究它的什么内容呢？

生1：平行四边形中的特例.

师：如何增加一个条件，使一个一般的平行四边形成为特殊的平行四边形呢？

生2：可以增加其中4个角为直角.

师：一定要4个角都是直角吗？这个限制条件能不能再精简呢？

生2：可以让邻角相等.

师：能再少吗？

生3：我认为有一个角是直角就够了.

师：为什么？能简单说说你的思考吗？

生3：平行四边形对角相等，邻角互补，有一个角是直角，其他三个角都是直角.

师：说得非常好！那还可以用其他方式增加条件，使一个一般的平行四边形成为特殊的平行四边形吗？

生4：可以让四条边相等.

师：一定要四边相等吗？能再精简吗？

生5：我认为邻边相等就可以了.

师：为什么呢？请说说你的理由.

生5：因为平行四边形对边相等，只要邻边相等，那么四边就是相等的.

师：同学们思考问题都非常全面！刚才我们从角的角度增加了“有一个角是直角”这一条件，呈现了特殊的平行四边形；然后，我们又从边的角度增加了“邻边相等”这一条件呈现了特殊的平行四边形. 今天这节课，我们先来研究增加“一个角是直角”这种特殊情况.

师：（实物模型演示）请同学们看我手中的平行四边形模型，我们观察左下角这个内角，在拉动它的过程中，平行四边形中的哪些量发生了变化？哪些量没有变？

生6：邊长没变，周长没变.

师：还有吗？

生7：内角和没变，外角和也没变.

师：哪些改变了呢？

生6：4个内角都变了.

生8：面积也变了.

生9：两条对角线的长度改变了.

生10：邻边的位置关系改变了.

……

师：同学们的观察能力很强，总结得也很全面！

片段2：矩形的定义和性质探究过程

师：你认为我们会对“矩形”按着什么顺序展开研究呢？

生众：定义-性质-判定-应用.

师：矩形可能在哪些方面具有特殊性质呢？

生11：边、角、对角线.

师：你为什么这样认为？

生11：因为平行四边形边、角、对角线有特殊性，矩形应该也是.

师：嗯！有道理！那么你打算如何研究矩形的性质呢？

生11：可以类比平行四边形.

师：请你说得再具体一点.

生11：就像学习平行四边形那样，我们可以先画图，然后观察图形，猜测边、角、对角线可能存在的关系，先用测量工具初步测量，最后用几何证明验证.

师：刚才这位同学说得非常好！我们研究几何图形的性质一般都是按照“观察-猜想-验证”这个顺序展开的. 现在请同学们就按着这个思路探究矩形的性质.

片段3：小结环节

师：同学们，这节课我们是通过怎样的方式进行学习的？

生12：我们是通过类比三角形、平行四边形学习经验来进行本节课教学的.

师：具体说一说，我们是如何类比的？

生12：我们根据三角形和平行四边形的学习经验知道平行四边形分别从“角”和“边”增加条件形成了两种特殊的平行四边形，确定了本节课的研究对象；然后我们又类比了平行四边形的性质内容，大致猜测了矩形的性质；类比了平行四边形的性质探究过程，确定了矩形性质探究的方法.

师：同学们总结得非常好！如果继续研究下去，你觉得接下来我们将研究什么？

生13：矩形的判定和应用.

师：那么，你猜测矩形的判定可以如何展开研究呢？

生13：类比平行四边形，写出矩形性质的逆命题，验证命题，形成定理.

生14：我觉得也可以从定义考虑，先证平行四边形再证有一个角是直角.

……

师：大家说的都有一定的道理，欲知后事，我们下节课见分晓！

矩形一课在本章中的教育教学价值

本节课的教学内容为矩形第一课时，研究的是矩形的概念和相关性质. 根据新课标的要求，矩形的性质不能只停留在知识教学上，而是要通过经历探索图形基本性质的过程，把发展学生的基本推理技能放在首要位置. 本节课教学前，学生已经学习了三角形、四边形、平行四边形，积累了一定的几何图形学习的经验，特别是在学习平行四边形时已经体会过一般到特殊的数学方法，也具有类比学习的经验. 本节课的内容既是前面所学平行四边形性质的运用，也是后面继续学习菱形、正方形性质的重要前提，为学习其他特殊平行四边形提供了相应的研究方法和学习策略，因此，在教材中起着承上启下的重要作用. 学生通过对已学平行四边形的特殊变化，类比一般的平行四边形自主抽象、探索得出矩形的定义和性质，矩形这节课的教学，不仅沿用了这个“基本套路”，还固化了“基本套路”. 如果说，在类比三角形研究过程展开四边形、平行四边形学习时，研究几何图形的“基本套路”生成了，那么在矩形这一课中这个“基本套路”更是生长了. 我们可以预测，在接下来菱形、正方形的学习中，这个“基本套路”的内涵会更加深刻与丰富.

对“矩形”教学相关问题的思考

1. 传承知识生长方式，注重“基本套路”教学

在本章教学时，笔者有意渗透类比思想，进行“基本套路”教学. 比如，在四边形的概念、要素、性质教学时，从类比三角形展开，从一般四边形到特殊四边形（平行四边形）的过渡，类比了一般三角形到特殊三角形（等腰三角形、直角三角形），教学四边形时，反复回忆三角形研究过程，形成几何图形研究的“基本套路”. 知识、方法自然生长，学生对于几何图形的研究方向已经很明确：定义-性质-判定-应用，如果继续研究下去，就是“一般到特殊”的深入研究，也就是探讨图形的特例. 在有了三角形和平行四边形的学习经验后，本节课矩形内容的教学环节自然流畅，水到渠成. 像这样，以类比思想作为知识生长的原动力，课前展示的那棵生长树，自然生长，枝繁叶茂，知识体系生机勃勃.

2. 类比矩形学菱形，自主探究辨异同

文章前面已经提到，矩形一课的教学为后面继续学习菱形、正方形性质埋下了伏笔，为学习其他特殊平行四边形提供了相应的研究方法和学习策略. 以菱形的性质教学为例，学生在片段1中已经初步感受到矩形性质的特殊之处是由于强化了平行四边形中一个内角条件，进而产生了牵一发而动全身的连带效应，引发了该平行四边形的邻边位置变化、对角线长短变化、形状变化等. 类比矩形，菱形性质的特殊之处也应该是强化了邻边条件产生，因此菱形必然会有相应的特殊性质，两者研究套路相同，但两个特殊的平行四边形，同中有异. 所以在学习菱形性质的过程中，既要类比矩形，也要对比矩形. 类比矩形，自然生长：研究路径相同，学生在菱形性质学习时会感觉轻车熟路；对比矩形，深化认识：体会到矩形和菱形作为平行四边形两个特例的特殊之处. 这样对比着学习有利于学生辨析两个特例图形各自的性质特征.

3. 动态展示一般到特殊，发展学生辩证思维

平行四边形到矩形的变化过程是一般到特殊的过程. 在動态展示这一变化的过程中，让学生感受并探究图形性质，既加深了学生对平行四边形性质的理解，体会何为形变质不变；又启发了学生对矩形性质的探究，形变质也变. 所以在教学矩形内容时，笔者注重引导学生观察动态变化的过程中，哪些性质保持不变，哪些性质发生了变化，这些发生改变的性质又是以怎样的规律在变化. 在此变化过程中，感受量变引起质变的哲学思想，丰富和完善学生的世界观，注重发挥数学学科育人的作用，培养和发展学生的核心素养.