错在哪里
2018-10-24 08:00:16俞天帅
中学数学教学 2018年5期
1 江苏省常熟市中学
俞天帅(邮编:215500)
问题(2013年第9期问题征解147)设正数x、y满足x3+y3=x-y,求使x2+λy2≤1恒成立的实数λ的最大值.
错解因为正数x、y满足x3+y3=x-y,所以x-x3=y+y3=y(1+y2)≥2y2.

解答错了!错在哪里?







2 广东省深圳市第七高级中学
曾玉婷(邮编:518104)
一元二次方程实根的分布问题,常作为考点之一出现于高考的选择或填空题,解此类问题需要考查学生的逻辑思维能力、运算能力. 罗碎海老师在其著作《高中数学问题探究》中的第5小节对根的分布问题进行详细介绍.
书中例3的第二小问给出解法一,之后指出解法有误,但并没说明为何有误,现提出问题供各位同行讨论.
例3a为何值时,方程x2+2(a-1)x+4=0分别有:(1)两正根;(2)两根都大于1(含等根).
解(1)略. 答案为a≤-1.


解答错了!错在哪里?

解法2


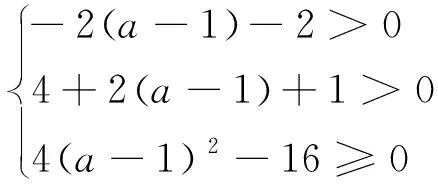
两种解法结构相似,为何解出来答案不同?而解法1有误,错在哪儿?
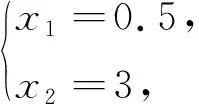
书中给出解法3:构造一元二次函数借用端点值、对称轴、对应判别式、开口解出a的取值范围. 此外还有一种解法:用求根公式把两根表示出来,令较小根大于1即可.
猜你喜欢
数理化解题研究(2020年8期)2020-03-30 09:13:54
中学数学杂志(初中版)(2020年6期)2020-01-06 03:35:20
幽默大师(2019年6期)2019-01-14 10:38:13
新教育时代·教师版(2018年17期)2018-07-21 09:39:38
上海预防医学(2018年2期)2018-03-27 06:41:14
祖国(2017年21期)2018-01-02 00:55:21
故事作文·高年级(2017年11期)2017-11-15 22:47:11
物理实验(2017年10期)2017-10-24 10:34:55
湖州师范学院学报(2016年2期)2016-08-21 13:50:52
中学教研(数学)(2015年3期)2015-12-08 08:11:49

