沙特阿拉伯JBMO不等式的两个漂亮证法

湖北省阳新县高级中学 (邮编：435200)

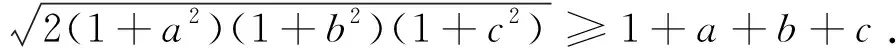
这是2017年沙特阿拉伯JBMO的一道不等式，左边有根号而右边没有，因此将左边根号去掉是解题的关键.下面介绍两个漂亮证法与读者分享.

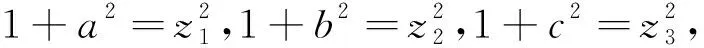
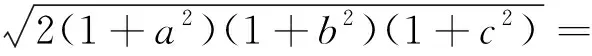
对任意实数x,y，我们有x2+y2≥2xy，则2(x2+y2)≥(x+y)2，

于是

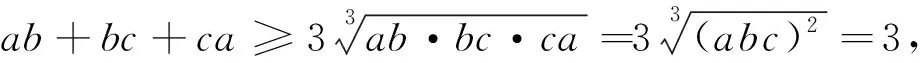
所以(ab+bc+ca-1)+(a+b+c-1)≥a+b+c+1，

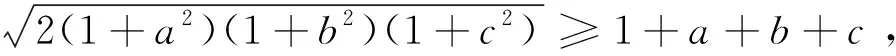
评注本解法根据四川熊昌进老师在《爱数集合》群里交流的解法整理而成.本解法首先根据题目结构特征构造复数，然后通过复数运算和模的性质，将所证不等式左边根号内的式子恒等变形为平方和的形式，接着用重要不等式的变式(即均值不等式)去掉根号，最后用三元均值不等式获得证明.

证法2由a,b,c>0且abc=1及柯西不等式得

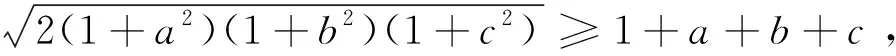
评注本解法根据深圳王扬老师和浙江张艳宗老师在《爱数集合》群里的交流思路和解法整理而成.本解法灵活巧妙，首先将左边根号内的三个因式的积，通过重组变为两个四项平方和的积，继而用柯西不等式一举获得证明，解法简洁流畅一气呵成.