蝴蝶定理解高考数学解析几何题的再探讨

安康学院数学与统计学院 (邮编：725000)

考题(2012年高考数学北京理科第19题)已知曲线C:(5-m)x2+(m-2)y2=8(m∈R).

(I)若曲线C是焦点在x轴上的椭圆，求m的取值范围；

(II)设m=4，曲线C与y轴的交点为A、B(点A位于点B的上方)，直线y=kx+4与曲线C交于不同的两点M、N，直线y=1与直线BM交于点G.求证：A、G、N三点共线.

文[1]在解题分析本题第(Ⅱ)中，指出学生用以下常规方法：

如图1，当m=4，椭圆C:x2+2y2=8与y轴交点坐标A(0,2),B(0,-2).

设直线y=kx+4与椭圆C交于不同的两点为M(x1,y1),N(x2,y2),由

(*)

(**)

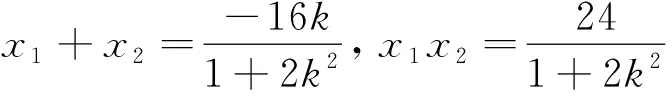
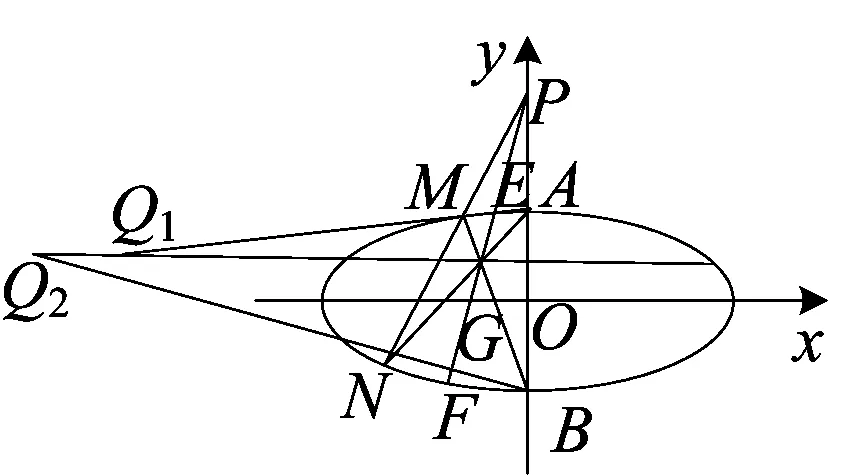
图1

由于考题图形具有“蝴蝶定理”的形式.文[1]利用蝴蝶定理给出新解法.对于利用蝴蝶定理证明命题，我们再进行探讨.

1 蝴蝶定理证明讨论

图2

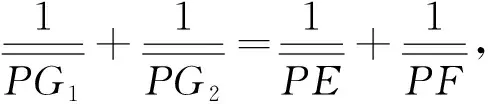
1.1 考题的证明

如图1，设直线对BM、AN相交于点G，直线PG交椭圆分别于点E、F，则由广义蝴蝶定理推论，得到

(1)

此时，设直线PG的方程为y=kx+4,结合椭圆方程，得：

(2)

则

(3)

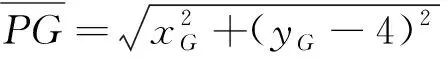
(4)

(5)

则由关系式(1)

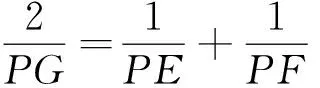
(6)

结合(3)，得

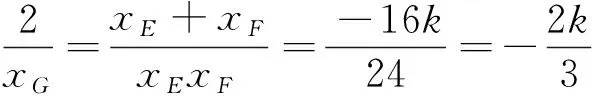
(7)

于是点G的y坐标满足：

yG=kxG+4=-3+4=1，

(8)

即直线对BM、AN相交于直线y=1.于是命题获得证明.

此方法的优点在于，无需直线PMN的斜率k，依然可以获得命题的证明.因此，此高考题可以修正为命题1.

命题1如图1.过椭圆C:x2+2y2=8外一点P(0,4)引C的割线PMN，直线对AN和BM交于点G，则点G的轨迹是定直线y=1

1.2 命题1 切点讨论

此时，设直线PMN方程为y=kx+4(k≠0)，结合椭圆方程，得

8k2⟺(1+2k2)y2-8y+16-8k2=0

(9)

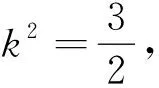
(10)

则当直线PMN与椭圆C:x2+2y2=8相切时，点G的y坐标满足：

(11)

即命题1的点G的轨迹(定直线y=1)经过直线PMN与椭圆C:x2+2y2=8的切点.

命题2如图1.过椭圆C:x2+2y2=8外一点P(0,4)，引C的交线PMN，直线对AN和BM交于点G，当交线PMN与椭圆C相切于点T1、T2，则点T1、G、T2共线于定直线y=1.

1.3 命题共点线的再讨论

现在，进一步讨论直线对AM和BN交于点Q的位置.

如图1.设直线y=1与椭圆C分别交于点E、F，交直线对AM、BN分别于点Q1、Q2，设直线AMQ1、BNQ2方程分别为y=k1x+2(k1>0),y=k2x-2(k2<0),则

(12)

由广义蝴蝶定理，得

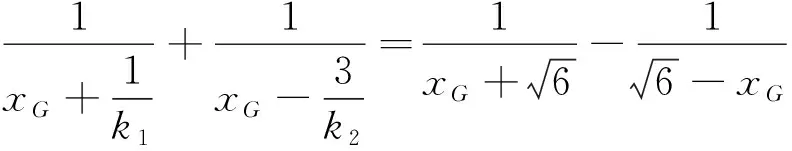
(13)

(14)

由直线对AN、BM方程：y=k3x+2(k3>0),y=k4x-2(k4<0),得

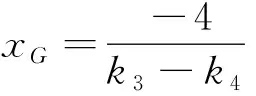
(15)

此时，由椭圆方程C,得

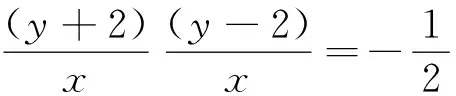
(16)

(17)

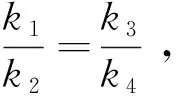
(18)

(19)

(20)

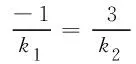
(21)

即直线对AM、BN相交于直线y=1.于是有结论.

命题3如图1，过椭圆C:x2+2y2=8外一点P(0,4)，引C的交线PMN，直线对AN和BM交于点G，直线对AM和BN交于点Q，当交线PMN与椭圆C相切于点T1、T2，则点Q、T1、G、T2共线于定直线y=1.

当然，对于命题1和命题3，也有简单的初等证明.

2 初等证明研究

2.1 对于命题1的证明

如图1，现设直线对AG、BM于点G，设直线PMN方程为y=kx+4,结合椭圆方程，得

(1+2k2)x2+16kx+24=0

(22)

则

(23)

对于共线的三点A、G、N和共线的三点B、G、M，有

(24)

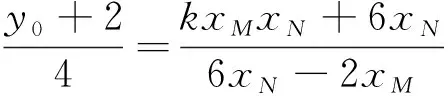
(25)

(26)

(27)

即直线对BM、AN相交于直线y=1.命题1获得证明.

2.2 对于命题3的证明

如图1.直线对AM、BN分别交直线y=1于点Q1、Q2，设直线PMN方程为y=kx+4,

结合椭圆方程，得

(1+2k2)x2+16kx+24=0

(28)

则

(29)

设直线AMQ1、BNQ2方程分别为y=k1x+2(k1>0),y=k2x-2(k2<0),则

(30)

(31)

现在，假设xQ1=xQ2,则(30)中的k满足

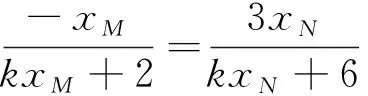
(32)

(33)

即直线对BM、AN相交于直线y=1.命题3获得证明.

2.3 命题中的直线斜率关系

在命题证明中，看到直线中的斜率具有多种关系.

命题4如图1.过椭圆C:x2+2y2=8外一点P(0,4)引C的交线PMN，直线对AN和BM交于点G，直线对AM和BN交于点Q.若设直线方程PMN为y=kx+4,直线方程PG为y=k′x+4,直线对AM和BN方程分别为y=k1x+2(k1>0),y=k2x-2(k2<0),直线对AN、BM方程为y=k3x+2(k3>0),y=k4x-2(k4<0),则直线斜率满足关系：

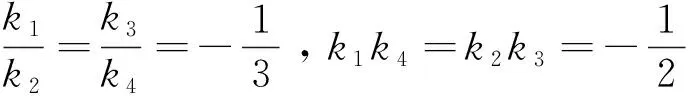
证明(2)由直线对NA、MB的斜率k3、k4关系，得

(34)

则结合(**)，得

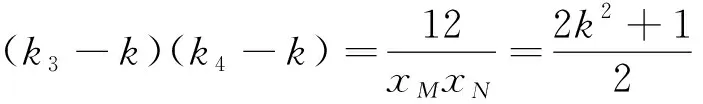
(35)

(36)

此结论是非常有趣，将斜率k3、k4换成斜率k1、k2,关系不变.即具有数学中的“不变量”关系.

(3)由直线对NA、MB的斜率k3、k4关系，得

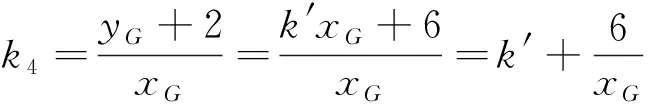
(37)

(38)

(4)在(36)和(38)中，取k4=-3k3,则

(39)