对一个猜想及其加强的简证

首都师范大学附属回龙观育新学校 (邮编：102208)北京市昌平区大东流中学 (邮编：102211)

文[1]中，梁昌金老师证明了三角形中关于外心、重心、垂心、内心的四个优美不等式，统一叙述如下：

在此基础上，在文末提出了一个猜想：

文[2]中，曹程锦老师首先指出文[1]的一点瑕疵，并将命题A做如下修改：

文[2]用五种方法完成了猜想的证明，并加强了猜想的结论：

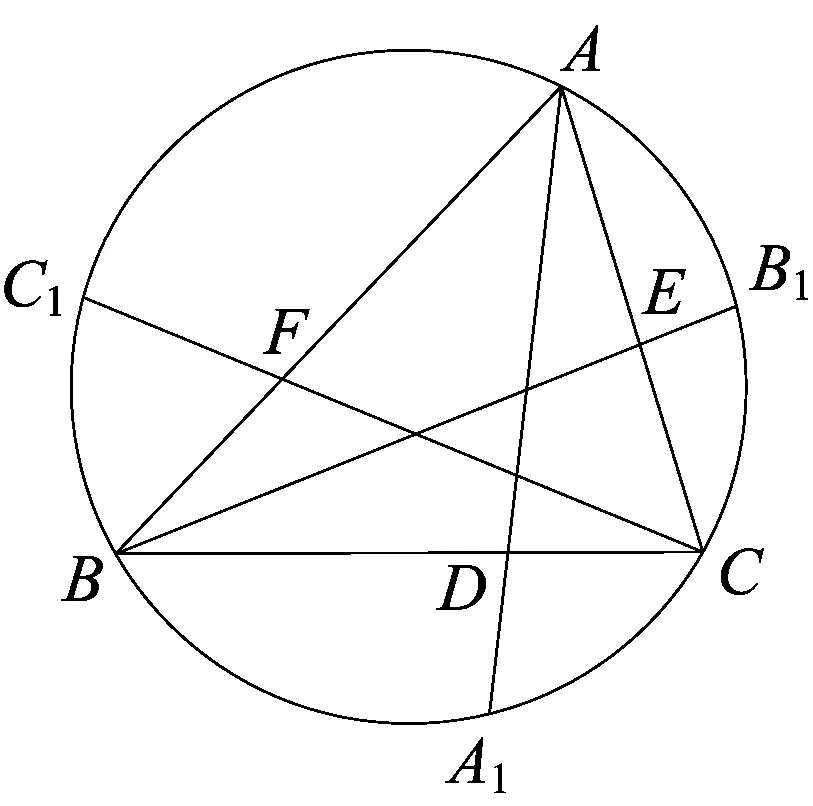
图1

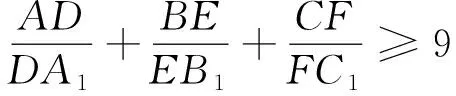
笔者认真学习了这两篇文章，获益良多，同时也有了一些自己的思考，通过探究，完成了猜想及其加强的简证．

1 文[2]中证法2的商榷

2 猜想及其加强的简证

为了证明猜想和其加强命题B，只需证明命题B.为此，先给出以下引理：

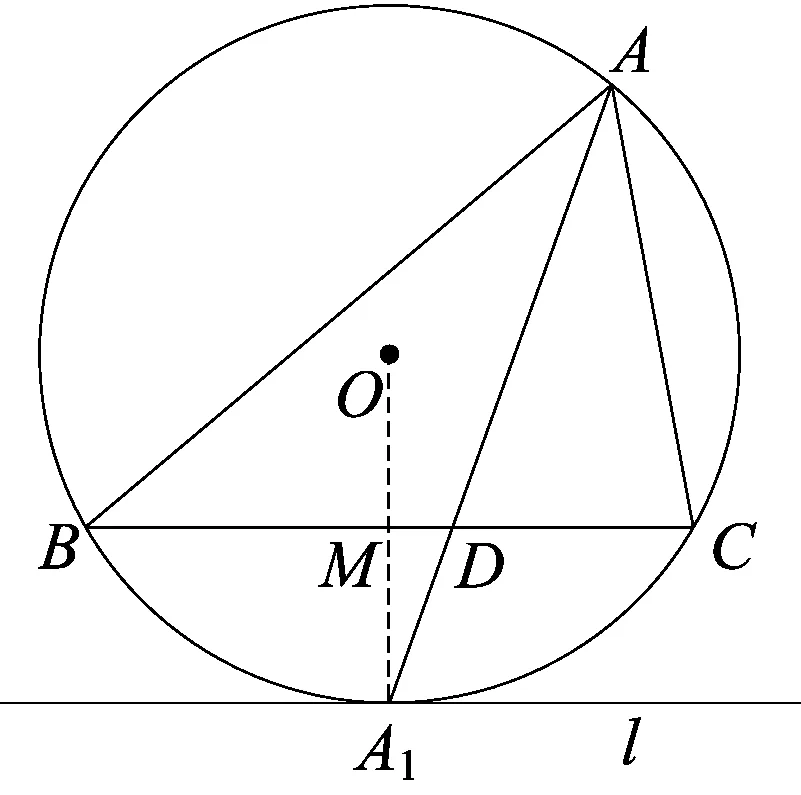
图2

引理如图2，设AD为△ABC的内角平分线，射线AD交△ABC的外接圆O于点A1,过A1作BC的平行线l,则l与圆O切于点A1.

证明连结OA1交BC于点M,由于AD为△ABC的内角平分线，则点M为线段BC的中点，由垂径定理，OA1⊥BC,因为BC//l,所以OA1⊥l,即l与圆O切于点A1.

命题B的证明

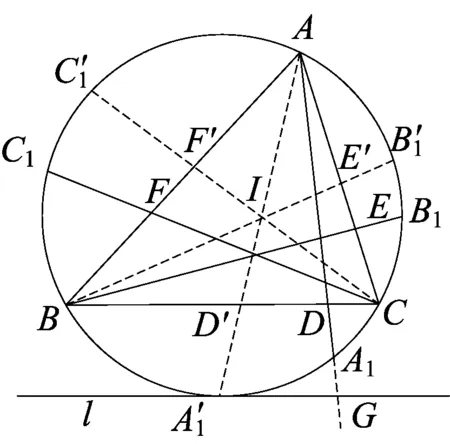
图3

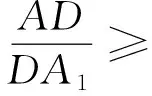
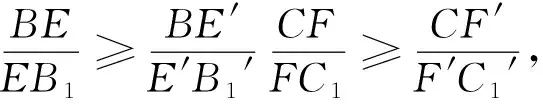
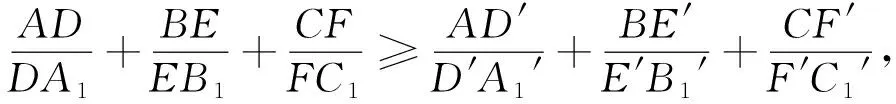
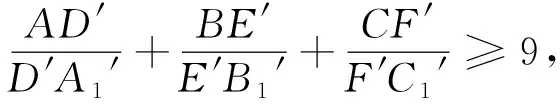
结合以上的证明及命题A的证明，当且仅当△ABC为正三角形，且AD、BE、CF交于△ABC的中心时等号成立.