余弦乐释“余怨”

湖南省长沙市周南雨花中学 (邮编：410014)

话说有一天，余弦发起了牢骚：

首先，从性质上讲：

性质正弦函数y=sinx(向左平移π2个单位)→余弦函数y=cosx单调增区间2kπ-π2,2kπ+π2 k∈Z 2kπ-π,2kπ k∈Z 单调减区间2kπ+π2,2kπ+3π2 k∈Z 2kπ,2kπ+π k∈Z 对称轴 x=kπ+π2k∈Z x=kπk∈Z 对称中心kπ,0 k∈Z kπ-π2,0 k∈Z

其次是化简求函数解析式时，全部化为正弦的形式.

(I)求f(x)的最小正周期；

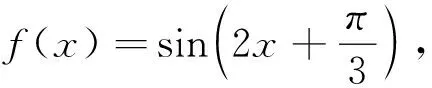
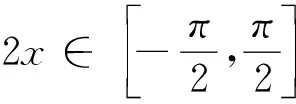
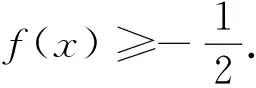
这是2017年北京高考文试题，也很简单，很快捷吧！

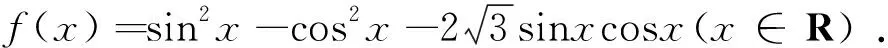
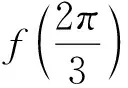
(Ⅱ)求f(x)的最小正周期及单调递增区间．

我就不信利用我不行！

故f(x)的单调递增区间为

这是2017年浙江高考试题，用我余弦来解答也一样方便快捷吧.

最可恨的是，连我和正弦的“二弦组合”形式，也变成只含有它正弦的形式，且其中的角还要由正切来确定，似乎与我余弦没有一点儿的关系.

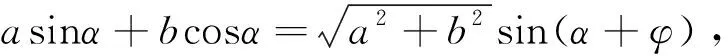
这个结论许多资料上称为“辅助角公式”，也是许多老师和同学津津乐道的一个最常用的三角公式，然而，我发现了它的一个不足.

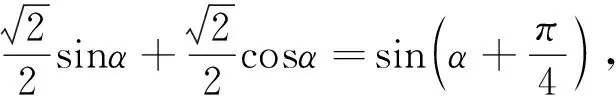
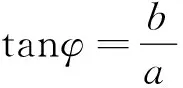
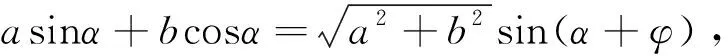
于是我将自己的怨恨和这个发现写信给这个老师，没有几天就收到了他的回信：

亲爱的余弦(函数)：

首先感谢你指出的这个错误，确实过去我们一直使用这个结论，没有注意到它是不严密的. 佩服你的钻研和思考精神，希望你一如继往，努力完善自己，多为社会做出贡献，也为学生的学习做出表率.

同时更重要的是要向你说声对不起，不是我“嫌弃”你，也不是我“抛弃”你. 而是因为学生的理解水平有限，让他们死记硬背你，还不如类比联想记忆你——紧扣你同“正弦”的形同特点——只需平移关系，这样学生对你的印象不是削弱了，反而更加强了，感觉你更生动，更形象，更有活力了. 其实数学的学习过程也是一个类比联想的过程，抓住知识点或数学概念之间的关联，就纲举目张，一通百通，举一反三. 在三角函数大家庭里，你们三兄弟，是相互联系的，血肉相连的，这一点从你们的定义和同角三角函数之间的关系也可以看出来，已知你们中的一个就可以求出另外一个，特别是你与正弦，更是唇齿相依的一衣带水的关系——如果唇亡，则一定齿寒，在许多实际问题的解答中也是需要你们相互配合，紧密相扣的.

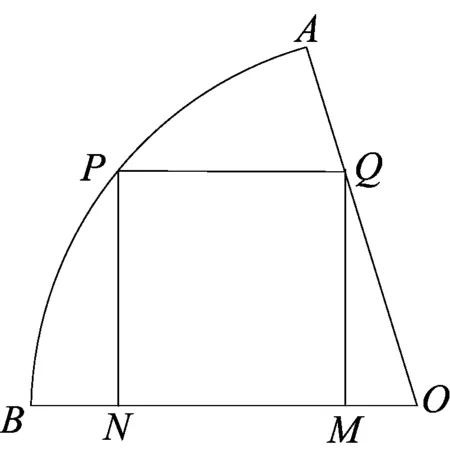
图1

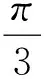
(1)设PN=x,将y表示成x的函数关系式；

(2)设∠POB,将y表示成θ的函数关系式；

(3)请你选用(1)或(2)中的一个函数关系式，求出y的最大值．

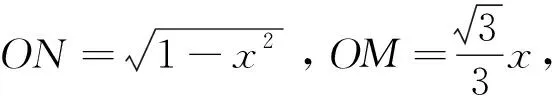
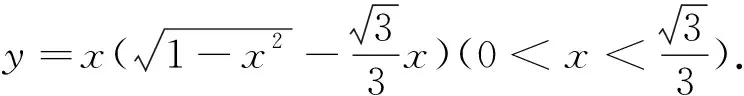
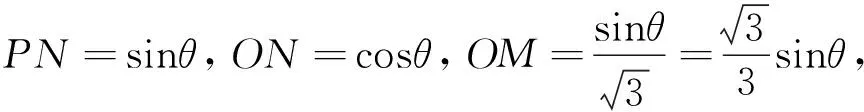
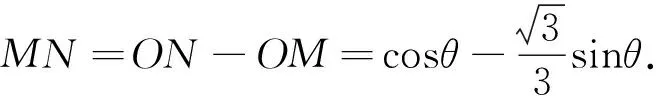
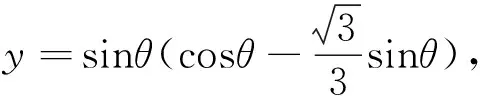
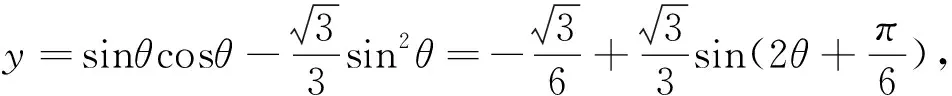
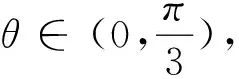
总结这里两种选择自变量的办法，一是以边长为自变量，二是以角度为自变量. 这两种方法都是抓住直角三角形，利用勾股定理或三角函数的定义，将相关量用自变量来表示，然后再根据面积或周长来建立函数关系式，但一定要注意函数式的定义域. 三角函数式中，一定要利用三角公式化为一个三角函数式，才能求出最大值.

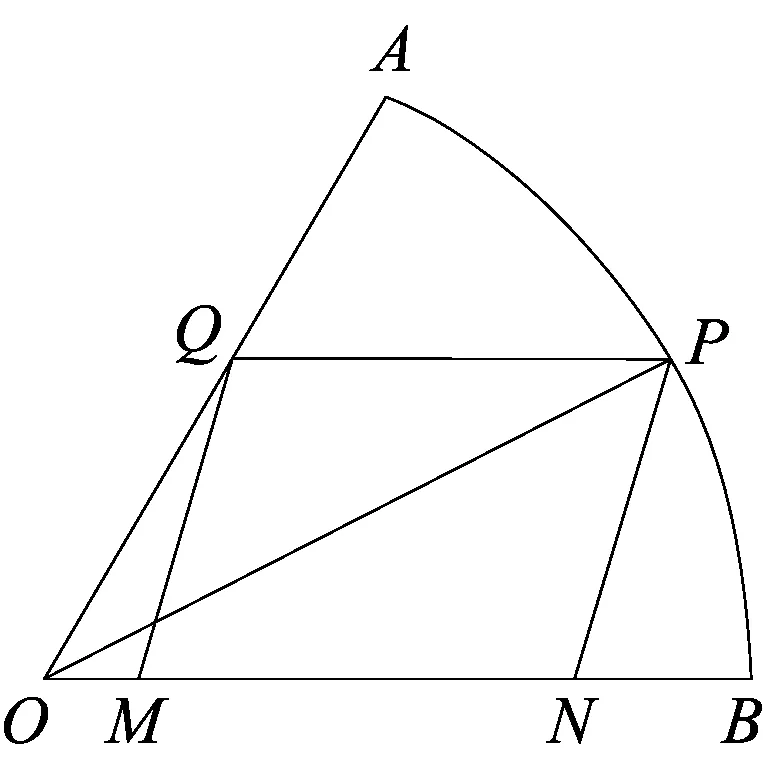
图2

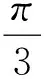
(1)求S关于θ的函数关系式；

(2)求S的最大值及相应θ的值．

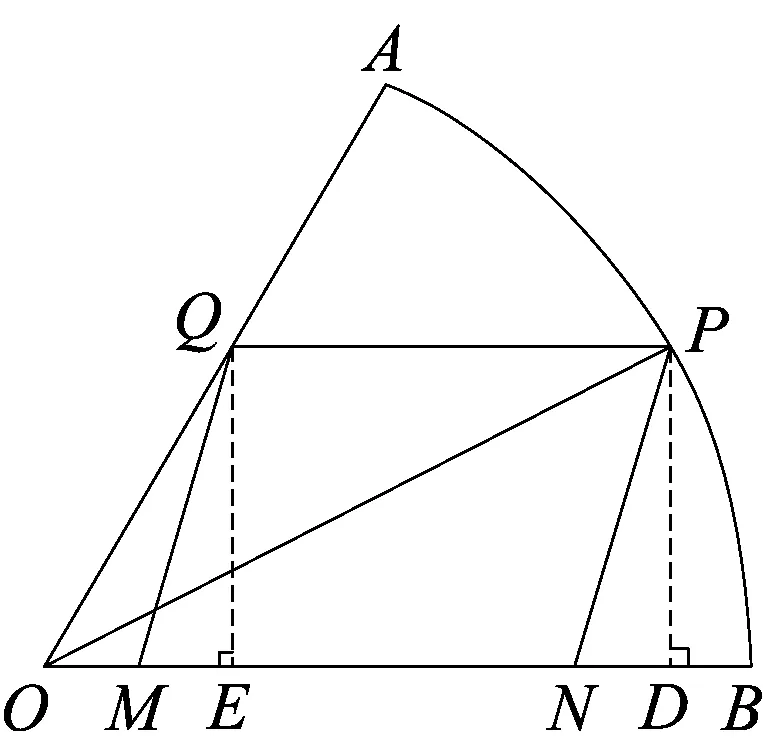
图3

解析(1)分别过点P,Q作OB的垂线，垂足分别为D、E,则四边形QEDP是矩形(如图3)．于是PD=sinθ,OD=cosθ.

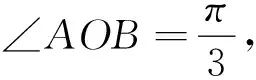
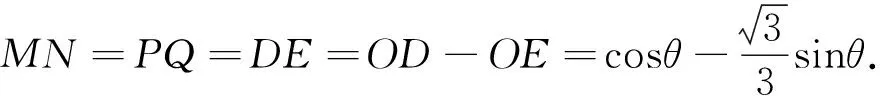
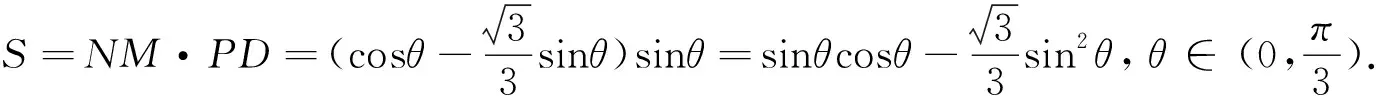
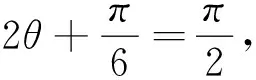
这是个内接平行四边形，先利用直角三角形内三角函数的定义求出平行四边形的边和高，将面积转化为三角函数式，再利用三角函数式来解决最值.

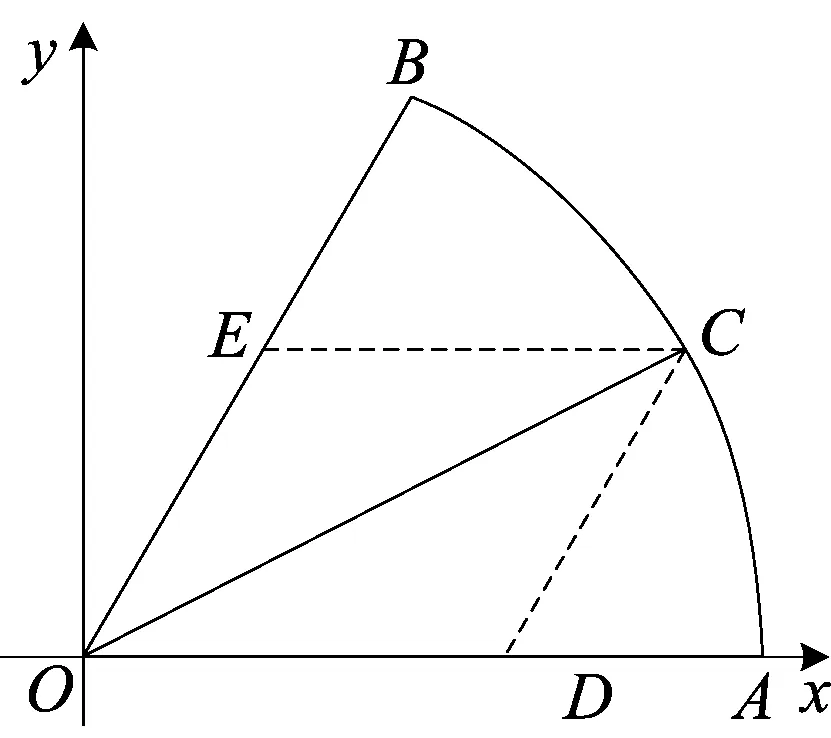
图4

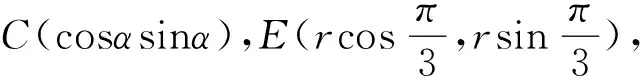
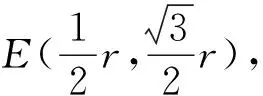
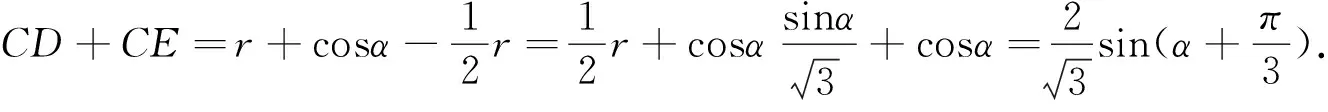
你看，这三个例题中离开了你余弦，能够解答吗？至少解答很不容易吧. 所以数学每个概念都是数学大厦的一块基石，在人类建筑现代文明社会中都不可或缺.

余弦看后，满脸惭愧，再也没有抱怨了，它甘愿做正弦，不，做所有数学概念红花的绿叶，为数学事业作出自己的贡献.