常数列在等比数列求和中的应用与推广
2018-09-22 02:51赵圣涛
数理化解题研究 2018年22期
赵圣涛
(山东省淄博市淄博中学 255000)
一、方法的提出——等比数列求和公式的推导
已知数列an是首项为a1,公比为q(q≠0)的等比数列,求该数列的前n项和Sn.
解(1)当q=1时,易知Sn=na1.
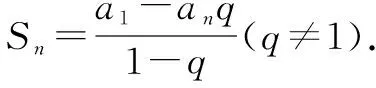
综上,由(1),(2)可知,等比数列前n项和的公式为
因为an=a1qn-1,所以上面的公式也可写成
因上述推导过程中的关键是如何构造常数列,所以本文将该方法称之为构造常数列法,该方法的特点是思路简洁,没有繁琐的运算,易于理解.
二、方法的推广
1. 问题提出
在数列求和的教学中,经常遇到如下题型:
已知数列an满足an=bncn,其中bn是公差不为0的等差数列,cn是公比不为1的等比数列,求数列an的前n项和Sn.
对上述数列an,结合自身特点,通常称其为等差乘等比型数列. 既然构造常数列法能在等比数列求和中应用,那么能否将该方法推广到等差乘等比型数列求和中去呢?经研究,这是切实可行的.
2. 问题解决
不失一般性,设等差乘等比型数列an的通项公式为an=(kn+d)qn(k≠1且k≠0,q≠0且q≠1),求数列数列an的前n项和Sn.
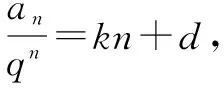
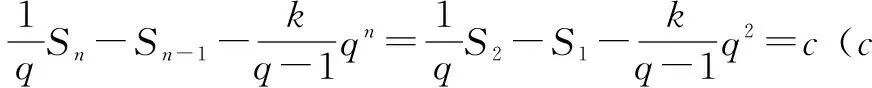



该方法思路清晰,运算量小,运算技巧远低于错位相减法和文[1]中所介绍的方法,有较强的实用性和可操作性. 同时该方法和常数列紧密地联系在了一起,进一步深化了人们对常数列的认识与理解.
三、方法应用
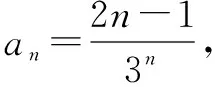
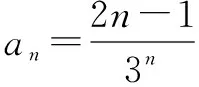
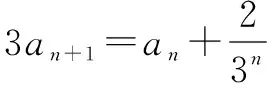

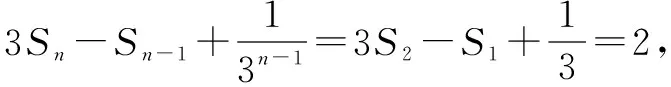
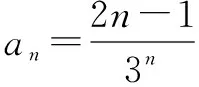
猜你喜欢
聊城大学学报(自然科学版)(2022年2期)2022-11-19
山西大同大学学报(自然科学版)(2021年3期)2021-06-24
中学生数理化(高中版.高考数学)(2019年10期)2019-11-08
中学生数理化(高中版.高二数学)(2019年9期)2019-09-28
中学生理科应试(2019年3期)2019-07-08
中学生数理化(高中版.高考数学)(2018年10期)2018-11-07
中学生数理化(高中版.高二数学)(2018年10期)2018-11-03
湖南教育·C版(2018年3期)2018-06-05
戏曲研究(2017年3期)2018-01-23
数学学习与研究(2017年14期)2017-07-20

