转化思想证垂直

赵佳琪

(河北省唐山市乐亭县第一中学高二三班 063600)

空间垂直关系有线线垂直、线面垂直、面面垂直，三者关系密切，可互相转化，在证明空间垂直时可谓三位一体．

一、证明线线垂直

空间中证明线线垂直，大都利用线面垂直的性质：如果一条直线垂直于一个平面，那么这条直线垂直于这个平面内的任意一条直线．但利用的前提是需有线面垂直.

例1 如图1，在空间四边形PABC中，PA⊥底面ABC，侧面PAB⊥侧面PBC．

求证：AB⊥BC．

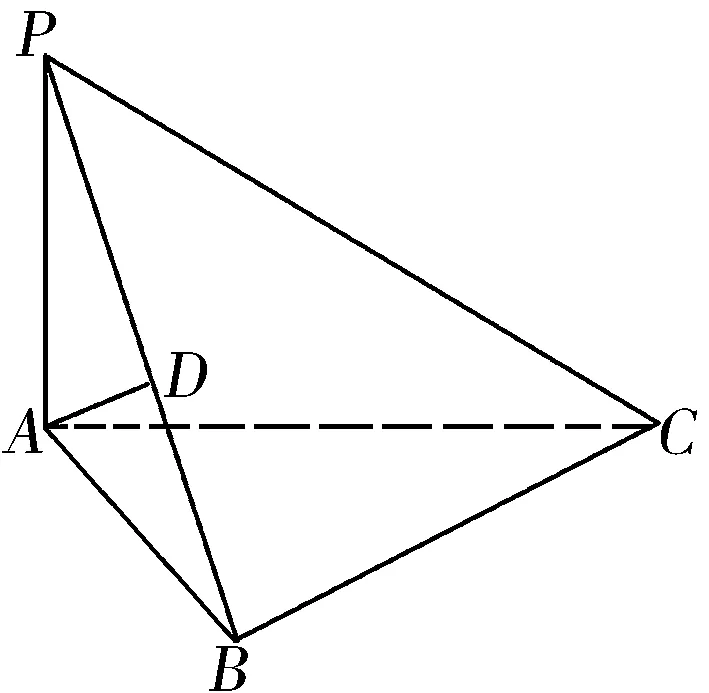
图1

分析我们可先证明AB(或BC)垂直于BC(或AB)所在的一个平面，即可证明AB⊥BC了．

证明过点A作AD⊥PB于点D.

因为侧面PAB⊥侧面PBC，

且侧面PAB∩侧面PBC=PB，

所以AD⊥平面PBC.

又因为BC⊂平面PBC，

所以BC⊥AD.

因为PA⊥底面ABC，BC⊂平面ABC，

所以BC⊥PA.

因为AD⊂平面PAB，PA⊂平面PAB，AD∩PA=A，

所以BC⊥平面PAB.

因为AB⊂平面PAB，

所以AB⊥BC．

点评本题的转化过程为：面面垂直→线面垂直→线线垂直→线面垂直→线线垂直，总的趋势是由高维向低维转化，其间应用了面面垂直的性质定理，线面垂直的判定定理及线面垂直的性质定理．

二、证明线面垂直

空间中证明线面垂直，常用的方法有两种：一是应用线面垂直的判定定理，一是应用面面垂直的性质定理．

例2 如图2，在斜边为AB的Rt△ABC中，过点A作PA⊥平面ABC，AM⊥PB于点M，AN⊥PC于点N，求证：PB⊥平面AMN．

图2

分析欲证PB⊥平面AMN，因为AM⊥PB，所以只需在平面AMN中再找一条和PB垂直的直线即可，考虑和AN有关的垂直关系较多，我们选定AN为论证目标．

证明因为Rt△ABC的斜边为AB，

所以BC⊥AC.

因为PA⊥平面ABC，BC⊂平面ABC，

所以BC⊥PA.

打仗要勇敢，搞学术研究为什么还要胆识呢？似乎两者关系不大，最近有记者问我，说阎老师你认为做一个研究员最重要的品格是什么呢？我的回答是两个字“勇敢”。

因为PA⊂平面PAC，AC⊂平面PAC，AC∩PA=A.

所以BC⊥平面PAC.

因为BC⊂平面PBC，

所以平面PAC⊥平面PBC.

因为AN⊂平面PAC，

平面PAC∩平面PBC=PC，AN⊥PC，

因为PB⊂平面PBC，

所以AN⊥PB.因为AM⊥PB，AM⊂平面AMN，

AN⊂平面AMN，AM∩AN=A，

所以PB⊥平面AMN．

点评本题的转化过程为：线线垂直→线面垂直→

面面垂直→线面垂直→线线垂直→线面垂直．

三、证明面面垂直

证明面面垂直离不开线线垂直和线面垂直．

例3 如图3，已知直角梯形ABCD中AB∥DC，∠DAB=90°，PA⊥底面ABCD．证明：面PAD⊥面PCD．

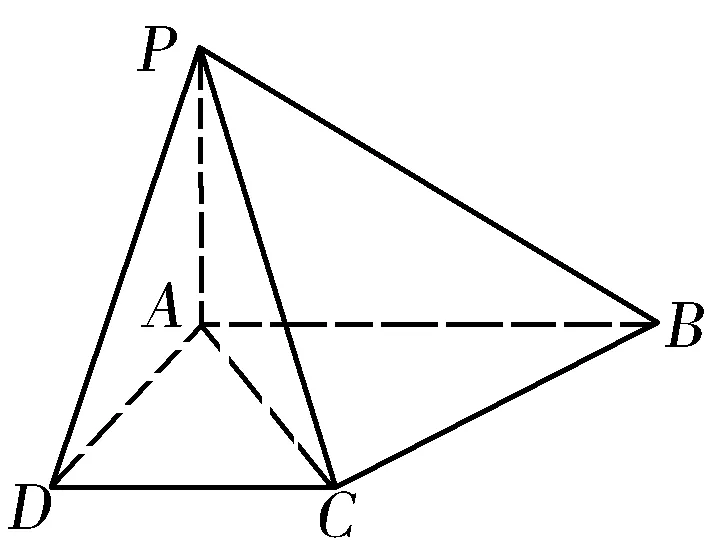
图3

分析根据题目条件可考虑利用面面垂直的判定定理证明．

证明因为PA⊥面ABCD，CD⊂面ABCD，所以CD⊥PA.

因为∠DAB=90°，AB∥DC，

所以CD⊥AD.

因为PA⊂面PDA，AD⊂

面PDA，PA∩AD=A，

所以CD⊥面PAD.CD⊂面PCD，

所以面PAD⊥面PCD．

点评本题的转化过程为：线面垂直→线线垂直→线面垂直→面面垂直．

立体几何中最常见的数学思想是转化思想，由本文我们可发现，证明垂直关系的过程实质上就是空间三种垂直关系相互转化的过程，转化的依据就是空间垂直的判定定理和性质定理，所以对这些定理我们一定要注意熟练掌握、灵活运用．