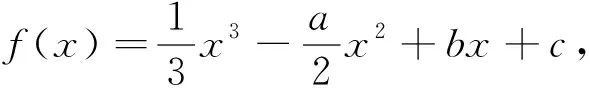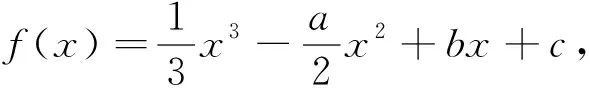三次函数有关极值的一个性质及应用

湖南省岳阳市华容县东山镇联校 (414203) 聂新军

设三次函数f(x)=ax3+bx2+cx+d(a≠0),记f′(x)=3ax2+2bx+c的判别式为Δ=4(b2-3ac).我们有如下结论:

命题1 对于f(x)=ax3+bx2+cx+d(a≠0),若Δ=4(b2-3ac)≤0,则f(x)无极值.

证明:因Δ=4(b2-3ac)≤0,当a>0时,f′(x)≥0,当a<0时,f′(x)≤0,均使f(x)为单调函数.故f(x)无极值.

命题2 对于f(x)=ax3+bx2+cx+d(a≠0),若Δ=4(b2-3ac)>0,记f′(x)=0的两根分别为x1,x2(x10时,f(x)的极大值M为f(x1),极小值m为f(x2),且M>m;当a<0时,f(x)的极大值M为f(x2),极小值m为f(x1),且M>m.

证明:当a>0时,由条件知当xx2时,f′(x)>0,当x10,a>0.

即M>m.

同理,当a<0时,f(x)的极大值M为f(x2),极小值m为f(x1),且M>m.

综上可知,我们有如下推论:

推论函数f(x)=ax3+bx2+cx+d(a≠0)有极值的充要条件是方程f′(x)=0有两个不相等的实根.

下面举例说明上述结论在解题中的应用.

例1 已知f(x)=ax3+bx2+cx,a+b+c=0,g(x)=f′(x),若g(0)g(1)>0,求证f(x)有两个极值.

例2 函数f(x)=x3+3ax2+3bx+c在x=2处有极值,其图像在x=1处的切线平行于直线6x+2y+5=0,求极大值与极小值的差.

解：f′(x)=3x2+6ax+3b,f′(x)=0有根x=2,所以4+4a+b=0①,由于图像在x=1处的切线平行于直线6x+2y+5=0,于是f′(1)=-3,即3+6a+3b=-3②,联立①,②解得a=-1,b=0,从而f(x)=x3-3x2+c.

令f′(x)=0,得另一根为0,由命题2知,当x=0时函数取极大值,当x=2时取极小值.于是所求之差为f(0)-f(2)=c-(8-12+c)=4.

例3 已知f(x)=3ax3+9bx2+9cx+15(a>0)在x=-2和x=4处取得极值,而极大值与极小值之差为27,求a,b,c的值.

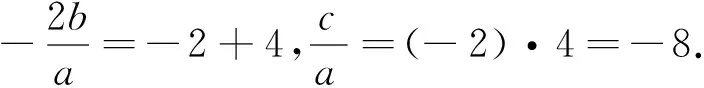
故b=-a,c=-8a.

例4 设函数f(x)=x3-3x2-8x,g(x)=x+a.若f(x)与g(x)的图像恰有三个交点,求实数a的取值范围.

解:f(x)与g(x)的图像恰有三个交点,即方程x3-3x2-8x=x+a恰有三个不等实根.令F(x)=x3-3x2-8x-x-a=x3-3x2-9x-a,只需F(x)的图像与x轴有三个不同交点.F′(x)=3x2-6x-9,易知F′(x)=0有两个不等实根x1=-1,x2=3,