一类含ex和lnx复杂结构的处理策略

江西省赣州中学 (341000) 廖志勇 李 斌

在赣州市模考考试中，文理科都有一道很有特征的导数压轴题，这类导数压轴题都含ex和lnx的复杂结构，本文拟从这类试题出发，归纳出处理这类试题的求解策略.

试题(2018年赣州市高三一模文科21)

(1)求a,b的值；

(1)求a,b的值；(2)证明：f(x)>1.

分析:这两个题目，都具有含ex和lnx的复杂结构，从这次考试学生得分的情况分析，很大一部分学生感觉处理复杂，利用整体构造函数求最值，求导复杂繁琐，难以求根,求解难度很大.那么，这类特征函数如何处理才能有效解决呢？首先要熟悉高考常考的重要函数的模型：

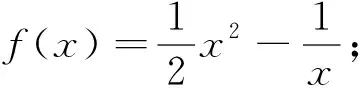
2.基于x(xn),ex四则运算组合模型.

3.基于x,lnx四则运算组合模型.

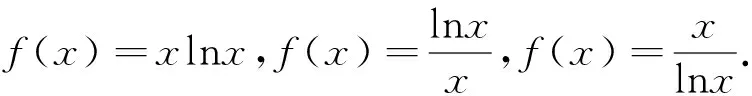
下面利用模型函数来解决这一类导数问题：

例1 已知函数f(x)=x2ex-lnx,证明：当x>0时，不等式f(x)>1.

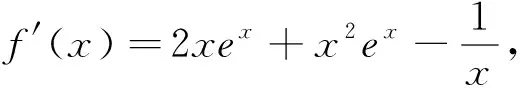
思考：分解函数时要尽量左凹右凸，最理想的状态是分离后函数的左边、右边都有最值.所以可以继续变形：

图1

(2)求a,b的值；(2)证明：f(x)>1.

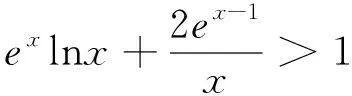
(1)求a,b的值；

分析：(1)a=b=-1.

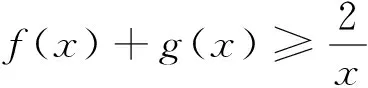
例4 (2018年赣州市高三一模理科.21)

设函数f(x)=a(x-lnx)-xe1-x.

(1)当a=-1时，讨论函数f(x)的单调性；

(2)若存在x≥1，使f(x)<1-x2成立，求实数a的取值范围.

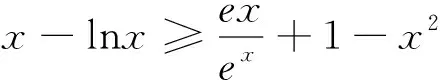
我们在解决含ex和lnx复杂结构导数问题，首先要熟悉xn,ex,lnx高考常见函数模型，明确其图形变化和最值；其次常常将这种复杂结构进行有效的分解，通过构造转化为常见函数最值的比较，从而使这类导数问题形成套路或策略.这类结构关键在于分解，分解的策略是尽量使不等式两边构造的函数左凹右凸，理想的状态是使不等式的证明转化成最值的比较.