对“证明函数不等式”问题的思考

四川省南充高级中学顺庆校区 (637000) 张小丹

在高中数学导数板块中，有一类常见问题：比较两个代数式的大小，如证明：f(x)≥g(x),x∈D.通常我们需要构造新函数h(x)=f(x)-g(x)，借助导数这一工具，通过研究函数h(x)在D上的最小值，去解决问题.然而，并非所有问题都能如此解决，如当函数h(x)的最值不易研究，或者最值不存在时，我们需另辟蹊径.

一、两个问题

(1)当a=1时，求函数f(x)的单调区间和极值；

思路1：构造函数，研究最值

分析过程意图设h(x)=f(x)-g(x)-12,x∈(0,e],则只需证明h(x)min>0构造函数,转化问题∵h'(x)=x2-x-1+lnxx2=p(x)x2,其中p(x)=x2-x-1+lnx,x∈(0,e].直接不好判断h'(x)的正负,引入p(x)则p'(x)=2x2-x+1x>0在x∈(0,e]恒成立,∴p(x)在x∈(0,e]上单调递增,∵p(1)<0,p(e)>0,∴存在唯一A∈(1,e),使得p(A)=0.研究p(x)的正负,零点存在,但不可求,将其虚设出来,用A表示.且当00,所以h(x)在(0,A)上单调递减,在(A,e]上单调递增.p(x)的正、负范围,对应着h(x)的增、减区间于是h(x)min=h(A)=A-lnA-lnAA-12.求出h(x)min由p(A)=0得A2-A-1+lnA=0⇒lnA=A+1-A2,所以h(A)=A2+A-1A-52.化简h(A)q(x)=x2+x-1x-52,10,所以q(x)在(1,e)上递增,…为判断h(A)的正负,构造q(x)

我们会发现，要想判断出h(A)的正负，关键在于进一步精确A的范围，但是在没有计算器的前提下，这并非容易之举，尤其是在时间有限的考试过程中.当我们发现此法并非优解时，要立即更变思路.

思路2：最值比较法

考虑求左、右两侧函数的最值，看能否求出

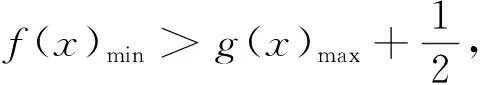
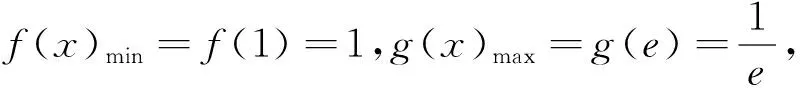
根据同学们反馈的情况，这道题全班只有几个同学勉强做对了，其他同学要么完全没有做，要么就是用他想到的办法进行了一半，发现走不下去了，就停了笔.而在这些没有做(对)的同学中，还有好多都是班上数学成绩比较优异的.

此法受阻，我们不妨考虑其他方案.

方案1最值存在与否可行与否求ex2-xlnx的最大值和xex+1e的最小值研究发现ex2-xlnx无最大值不可行

方案2最值存在与否可行与否求ex2-1e的最大值和xex+xlnx的最小值研究发现ex2-1e无最大值不可行

方案3最值存在与否可行与否求ex2-xex的最大值和xlnx+1e的最小值研究发现xlnx+1e有最小值0,且ex2-xex≤0可行

经过方案1、2、3的探讨，我们最终敲定方案3，并按此执行.

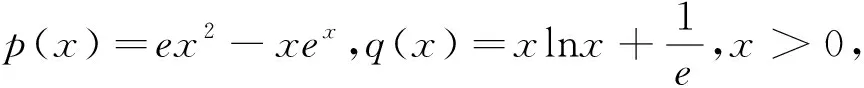
二、相互关系

对于题目1，先抛开解题成功与否，就运算量而言，思路2显然更胜一筹.但遗憾的是，f(x)>g(x)与f(x)min>g(x)max二者间的关系并非充要.换句话说，我们可以由f(x)min>g(x)max，得到f(x)>g(x)，但无法由f(x)>g(x)得到f(x)min>

g(x)max(如图2)，即“f(x)min>g(x)max”是“f(x)>g(x)”的充分不必要条件.

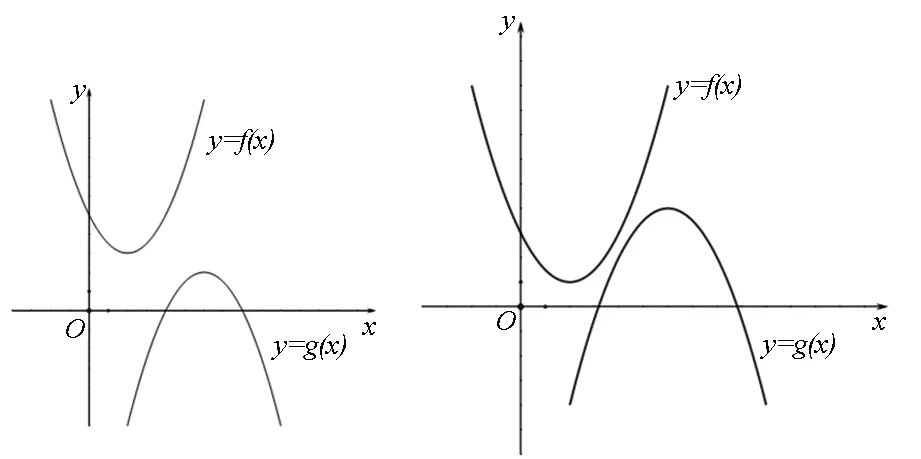
图1 图2

三、反思与总结

对于f(x)>g(x)(或f(x)≥g(x)的证明，我们可以考虑以下思路：

①构造h(x)=f(x)-g(x)，研究h(x)的最小值；

②若①中的h(x)的最小值不容易得出，或者不存在，则考虑③；

③尝试求f(x)min,g(x)max，看是否有f(x)min>g(x)max(或f(x)min≥g(x)max；

④若③失败，即f(x)或g(x)最值不存在，或不易求出，则考虑将不等式f(x)>g(x)等价变形(通分、移项，或者换元等)，转而证明不等式p(x)>q(x)，再研究p(x)min,q(x)max.