等差、等比数列的通项及前n项和性质及应用

宁夏彭阳县第四中学 (756599) 李艳玲

文[1]通过对等差数列前n项和的研究得出了一条结构优美、形式简洁的性质，同时用此性质简解了一些与性质相关的数列习题.读文颇受启发，但遗憾之处，感觉到形只影单，笔者对等差、等比数列的通项及前n项和进行系统研究得到了与文[1]性质相类似的几个性质.

性质1 已知数列{an}是等差数列，则有(r-t)am=(m-t)ar-(m-r)at，其中m,t,r∈N*且t≠r.

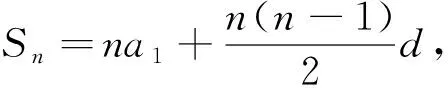
性质3 已知数列{an}是正项等比数列，则有(r-t)logaam=(m-t)logaar-(m-r)logaat，其中a>0，m,t,r∈N*且a≠1，t≠r.

性质4 已知Sn是等比数列{an}的前n项和，q≠1为{an}的公比，则有(qr-qt)Sm=(qm-qt)Sr-(qm-qr)St，其中m,t,r∈N*且t≠r.

例1 在等差数列{an}中，am=n，an=m，且m≠n，求am+n.

解:令m=m+n，t=m，r=n代入性质1得(n-m)am+n=(m+n-m)m-(m+n-n)n，化简得(n-m)am+n=0，又m≠n，所以am+n=0.

例2 设等差数列{an}的前n项和为Sn，若Sk-1=-2，Sk=0，Sk+1=3，则k=( ).

A.3B.4C.5D.6

例4 各项为正数的等比数列{an}的前n项和为Sn，若Sn=2，S3n=14，则S4n等于( ).

A.80B.30C.26D.16

例5 设等比数列{an}的前n项和为Sn，若S3+S6=2S9,求数列{an}的公比q.

解:由已知q≠1，令m=9,t=6,r=3代入性质4得(q3-q6)S9=(q9-q6)S3-(q9-q3)S6⟹S9=-q3S3+(q3+1)S6⟹S9-S6=q3(S6-S3).(*)