在反思中探究，在探究中提高——例谈高三复习课的教学

浙江省慈溪市周巷中学 (315324) 朱建治

高三教学基本上就是复习，复习就离不开做题，讲题，是就题论题还是借题发挥，笔者认为高三复习的课堂定位应侧重在学生认知的基础上，如何充分调动学生的积极性、如何引导学生进行自觉反思、如何在反思中探究，进而提炼、创新，从而达到知识的构建.本文将谈谈一堂在反思中作探究的复习课教学实践.

环节1:一题多解，感悟通法

例1 (2016浙江调研卷)已知抛物线关于x轴对称，它的顶点坐标在原点，点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.

(1)写出抛物线的方程;

(2)当直线PA与PB斜率存在且倾斜角互补时，求y1+y2的值及直线AB的斜率.

解答：(1)y2=4x.

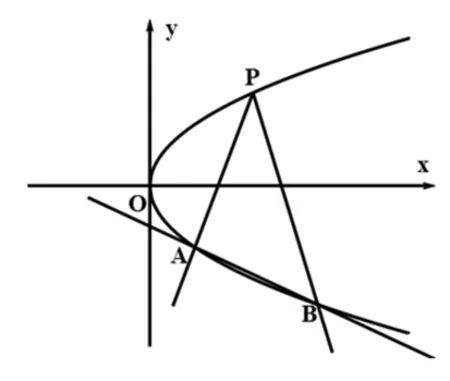
图1

题目背景：这是一个非常经典的定值，定点问题，在历年学考，高考中屡有出现，其中也有好多现成的结论，对学生来说，没出现过的都是新的，对教师来说是一个不可多得的教学素材，因此要利用好这个素材.

解法分析：方法一通过设直线PA与PB的方程，然后与抛物线联立，利用韦达定理解得A,B坐标，求出斜率，思路自然流畅.方法二利用抛物线上点的特殊性可以把两点的斜率用一种字母表示，避开了方程组的联立，简化了计算，是抛物线中一种常用的，有效的通法.方法三设直线AB的方程为y=kx+m，与抛物线联立消x，利用y1+y2=-4为常数解得斜率k的值.这是直线与圆锥曲线解答题中，非常普遍的一种直线方程设法.但是对于一些计算弱的同学来说，引进两个变量从心理上有点排斥，需要我们在课堂上多进行有效的训练.通过三种方法的解答，让学生感悟解析几何中的通性通法，感受抛物线的特殊性，从而达到知识的构建.

环节2:追本溯源，反思探究

波利亚在解题理论中指出：解题需要回顾，通过反思自己的解题过程，思考无论是在解题过程中的某些问题，还是最终的结论，提出有价值的问题.罗增儒教授指出，解题完成以后，结论也是一种条件.因此通过对解法的回顾及结论的反思，师生共同作如下反思与探究.

反思1：由结论可知直线AB的斜率为定值，那么该定值是否与点P有关？若有关能否得到一般性结论?

反思2：定值直线AB的斜率,是否具备某种几何性质？

图2

分析：运用极限的思想，如图2，观察到当A,B两点无限接近时，直线即为抛物线在P'(x0,-y0)处的切线，因此该定值即为切线的斜率,从而学生对该定值产生直观的认识，认清了问题的本质.

反思3:与“直线PA与PB斜率存在且倾斜角互补”这一语句，叙述等价的自然语言还可以怎么表述？

分析：读懂自然语言的表述是审题的关键，因此掌握语言的表述至关重要，该语句还可以表述为：“过点P作x轴的垂线，其恰好是∠APB平分线”; “直线PA与PB分别交x轴于C,D两点，ΔACD为等腰三角形”；“直线PA与PB关于直线y=y0对称”等等.

反思4:若kAB=-1，P(1,2),A(x1,y1),B(x2,y2)在抛物线上，直线PA与PB斜率存在时，问倾斜角是否互补？

分析：显然这是结论与题设的互相交换，是命题中的常用方法，经计算，当kAB=-1时，可以得到kPA+kPB=0，所以倾斜角互补.这种变式在平时应该多反思，多尝试，多训练.

反思5:若已知斜率为定值-1的直线AB与抛物线交于A,B两点，是否在抛物线上存在定点P,使得kPA+kPB=0？

分析：题设与结论互相交换，把定值问题又转化为定点问题，经计算，存在定点P(1,2)，使得kPA+kPB=0.通过这样的变式反思，学生能把问题看得更清楚，更全面.从而学会自己提出问题，并解决问题.

针对以上的反思，从题设的关键词入手，在教师的引导下一起作出如下的探究问题.

探究1 不改变题设的其他条件,第二问改成满足条件kPA+kPB=1(为了计算方便故取和为1)，那么直线AB的斜率还会是定值吗？

分析：利用方法一和方法二的运算，发现直线的斜率不是定值了，再利用方法三的运算：设直线AB的方程为y=kx+m,联立

探究2 若满足条件kPA·kPB=1(为了计算方便故取积为1)，直线AB又具备什么性质？

分析：同探究1，通过计算容易发现直线AB的斜率也不是定值，且计算得到直线AB过定点(-3,-2).

探究3 由探究1、2你能大胆猜想一般的情况吗？

分析：探究3由于时间关系，不作课堂上处理，只是提出问题，并猜想：斜率和为定值，斜率积为定值时，直线具备过定点的性质，有兴趣的同学课后自行探究一般情况，无需记忆.因为涉及直线与圆锥曲线的性质有上百条，避免增加学生负担，不可能都去记忆.笔者认为了解问题的背景，掌握处理问题的方法比记一些结论更有效，这也是本堂课的目标所在.

探究4 过抛物线内一定点(3,-2)的直线交抛物线于A,B两点，问kPA·kPB是否为定值？

分析：还是条件与结论互换，通过计算容易得到kPA·kPB为定值-2.

探究5 类比椭圆与双曲线是否也能得到类似的结论(课后探究)？

分析：圆锥曲线的性质往往具备相通性，同样的问题在不同的曲线中经常会有共同的解法和共同的性质，让学生学会用联系的观点看问题，达到融会贯通.

环节3:考题再现，收获成功

图3

例2 (2017浙江4月学考)如图3,已知抛物线C:y2=2px过点A(1,1).

(1)求抛物线C的方程；

(2)过点P(3,-1)的直线与抛物线C交于M,N两个不同的点M,N(均与点A不重合).设直线AM,AN的斜率分别为k1,k2，求证：k1·k2为定值.

解： (1)y2=x(过程略).

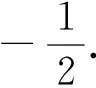
有了前面的反思与探究，再回顾这个学考题，如同囊中取物，唾手可得！学生的积极性与自信心得到极大的激发.

课后反思：圆锥曲线是历年高考的重点，也是整张试卷得分的分水岭，因此在复习中如何高效复习一直是一线教师的困惑，并为之努力追求效益最大化.本节课共2课时，让学生经历知识的发生发展过程，达到两个目标，其一：体会在直线与抛物线的综合运用中，直线方程的设法对解题的影响，提高运算能力，掌握通性通法：其二：通过对一个定值问题的反思，认清问题的来龙去脉，展开一系列的探究，初步掌握一类定值问题和定点问题的解决方法.通过两个目标的达成，让学生学会反思，学会探究，掌握解决直线与圆锥曲线的一般处理方法.课堂实践证明这是一种行之有效的复习方式.