一道高考题探究出抛物线焦点弦几个结论
山东省聊城大学数学科学学院 (252000) 张 鑫 于兴江
抛物线的焦点弦问题,一般采用韦达定理,采取设而不求.本文以2017年全国高考理科I卷第10题为例,利用几何画板探究了抛物线中焦点弦的几个结论.
2017年全国高考(理)Ⅰ卷第10题:已知F为抛物线C:y2=4x的焦点,过F作两条相互垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为( ).
我们利用几何画板探究得到.
定理1 已知F为抛物线C:y2=2px的焦点,过F作两条相互垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为8p.
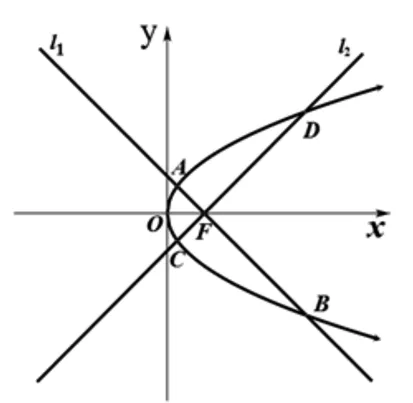
图1
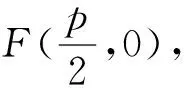
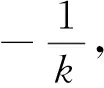

设点A(x1,y1),B(x2,y2),D(x3,y3),E(x4,y4),

注:2017年全国高考(理)Ⅰ卷第10题中抛物线C的方程为y2=4x,即p=2时,F为抛物线C:y2=4x的焦点,过F作两条相互垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为16.

图2
定理2 已知F为抛物线C:y2=2px的焦点,过F作两条相互垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|·|DE|的最小值为16p2.

定理3 已知F为抛物线C:y2=2px的焦点,过F的直线l交抛物线于A、B两点,A、B两点在抛物线准线上的射影为A1、B1,连接A1B与AB1,则A1B与AB1经过原点.

图3
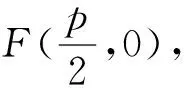

y2-2pky-p2=0.




图4


设点A(x1,y1),B(x2,y2),由韦达定理得,
圆锥曲线问题是高中重点数学知识,也是高考必考题之一,学生可以通过一道圆锥曲线的题目探究出圆锥曲线的一类问题,本文以探究抛物线的焦点弦问题为例,逐步培养学生的创新意识,提高探索及解决问题的能力.

