绝知此路不虚探 又得曲线一共性*——一道高考数学题的多角度探究与拓展

●

(贵州师范大学，贵州 贵阳 550025)

1 试题呈现

高考试题凝聚了命题人的心血和时代的理念，每一道试题都经过命题者的反复考量与打磨.解析几何中主要蕴含的数学思想是借助平面直角坐标系，用代数的方法来研究几何问题，这就体现了解析几何具有代数与几何的双重身份.圆锥曲线是解析几何的重要部分，对于圆锥曲线问题的解决，教师应培养学生从代数和几何两大维度进行多方面探究和思考，从而达到培养学生数学核心素养的目的.“课堂教学要立足基础，高于基础，挖掘本质，探寻联系，这也是素质教育的一种体现”[1]，本文以2018年全国数学高考卷Ⅰ理科试题第19题的第2)小题为例，探讨解题策略，并进行推广.

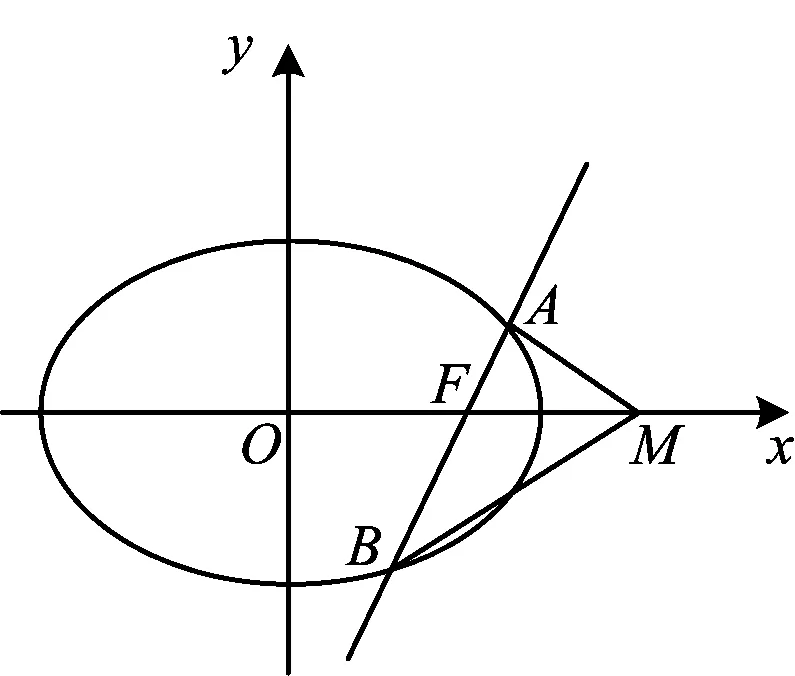
图1

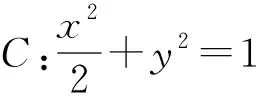
1)当l⊥x轴时，求直线AM的方程；

2)设O为坐标原点，证明：∠OMA=∠OMB.

(2018年全国数学高考卷Ⅰ理科试题第19题)

分析这是一道经典的圆锥曲线试题，其特点体现在：椭圆与直线的结合、直线过椭圆的焦点、定点M、求证两角相等，有着较强的几何意味.要解决此问题，通常有3个视角：1)将几何问题转化为代数问题，用代数的方法解决此问题；2)从几何的角度解决问题，用图形的代数特点帮助达成几何目标；3)两者的折中，几何与代数相互交融，互相补充，最终解决数学问题.

2 解题策略

2.1 代数视角

根据学生的已有认知结构，要说明两条直线与x轴的夹角相等，从代数的角度就是要说明两直线的斜率互为相反数，因此较容易想到如下证法：

证法1(将角度关系转化为斜率关系)设直线AM，BM的斜率分别为k1，k2，分情况讨论：

由第1)小题可知，当直线l⊥x轴时，k1=-k2，即直线AM，BM的斜率互为相反数，倾斜角互补，故∠OMA=∠OMB.

当直线l与x轴不垂直时，设直线l:y=k(x-1)，点A(x1,y1)，点B(x2,y2)，联立

得

(2k2+1)x2-4k2x+2k2-2=0,

从而

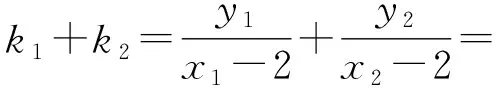
即直线AM，BM的斜率互为相反数，倾斜角互补，故∠OMA=∠OMB.

证法2(巧设直线方程，简化计算)设直线AM，BM的斜率分别为k1，k2，分情况讨论：

当直线l与x轴重合时，∠OMA=∠OMB=0°；当直线l与x轴不重合时，设直线l:my=x-1，设A(x1,y1)，B(x2,y2)，联立

得

(m2+2)y2+2my-1=0，

从而

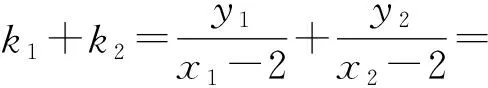
即直线AM，BM的斜率互为相反数，倾斜角互补，故∠OMA=∠OMB.

评注以上两种证法本质上是一样的，都是通过联立方程表示出点A，B坐标之间的关系,根据一元二次方程根与系数的关系，结合两直线的斜率表达式，最终证明两直线的斜率互为相反数，从而得出问题的证明.证法2相对于证法1是在数学运算上的改进，改变了直线l方程的设法，适当简化了运算过程.

2.2 几何、代数融合的视角

代数视角通过证明两直线的斜率相等得出证明，方法直接，运算却稍显复杂.该视角下让几何与代数适度融合，将两角相等转化为两角的正切值相等或点到直线的距离相等的问题，再用代数的方法计算线段的长度，在一定程度上降低了计算难度.

证法3(利用两角正切值求证两角相等)假设直线l的斜率存在，设其方程为y=k(x-1)，设A(x1,y1)，B(x2,y2).要证∠OMA=∠OMB，只需证明tan∠OMA=tan∠OMB即可.

由题意可知M(2,0)，从而

于是

即

(2-x1)y2=(x2-2)y1.

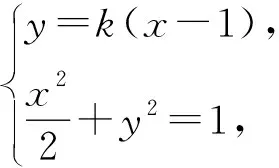
进而 (2-x1)y2-(x2-2)y1=

-2kx1x2+3k(x1+x2)-4k=0,

即

tan∠OMA=tan∠OMB,

故

∠OMA=∠OMB.

图2

k(x1-1)x-(x1-2)y-2k(x1-1)=0，

k(x2-1)x-(x2-2)y-2k(x2-1)=0.

要使∠OMA=∠OMB，只需d1=d2,d1,d2是点F到MA,MB的距离，其中

假设d1=d2，即

两边平方,得

于是d1=d2，故∠OMA=∠OMB.

评注以上两种方法直接从两角相等的几何意义入手，思路清晰，凸显几何和代数之间联系的紧密性，使得数学运算得到了简化.

2.3 几何视角

要证明两个角相等，可将要证相等的两个角构造于两个三角形中，通过证明两个三角形相似，进而得到两个角相等.

图3

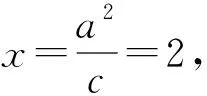
作椭圆的准线l:x=2，过点A作AD⊥l于点D，过点B作BE⊥l于点E.根据平行线分线段成比例，得

即

从而在Rt△ADM与Rt△BEM中，tan∠AMD=tan∠BME，即

∠AMD=∠BME，

故

∠OMA=∠OME.

评注以上方法思路清晰，步骤简洁，几乎没有复杂的代数计算.究其原因:一方面是因为点M的特殊性——恰好为准线与x轴的交点，由此便可借助椭圆的第二定义；另一方面是借助几何方法——平行线分线段成比例定理、相似三角形性质.由此再次验证在解析几何中，借助几何方法，往往能够简化问题解决的运算过程.

3 推广结论

综上所述，本题第2)小题中所要证明的∠OMA=∠OMB，从5个角度入手均可证.由证法5可知，利用椭圆第二定义是证明∠OMA=∠OMB的关键，主要考查学生对于椭圆性质和定义的掌握以及应用.在高中阶段椭圆、双曲线、抛物线相关性质和定义构成了圆锥曲线的知识框架，根据相似三角形的性质，借助椭圆第二定义(即证法5)解决第2)小题得到启示：

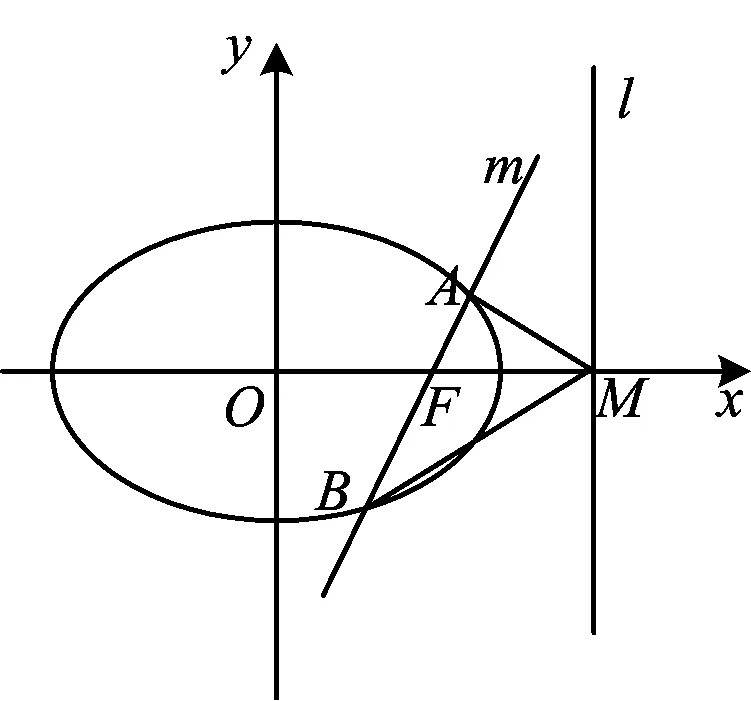
图4

证明同证法5(略).

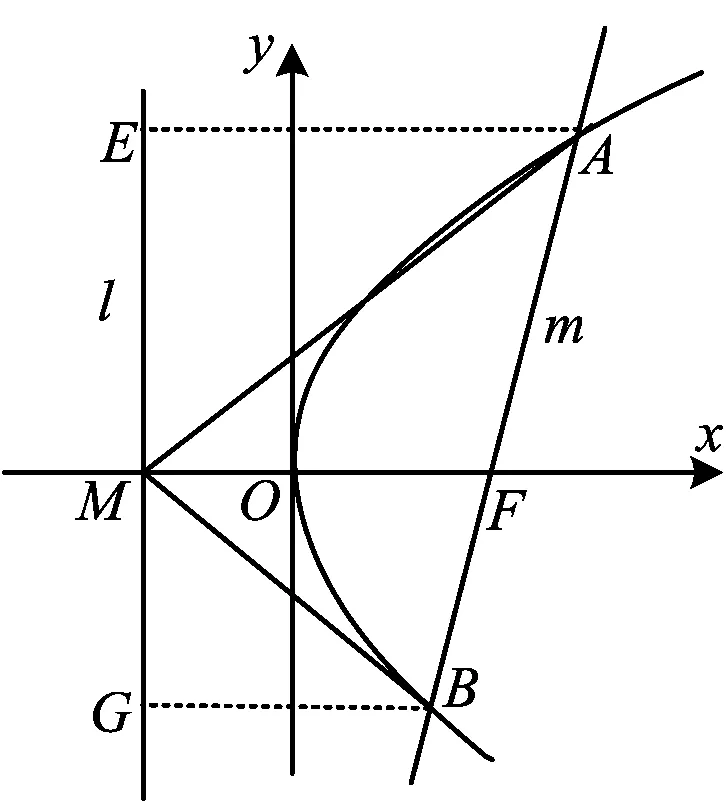
图5

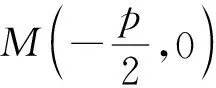
证明如图5，过点A作AE⊥l于点E，过点B作BG⊥l于点G.根据平行线分线段成比例，得

从而在Rt△AEM与Rt△BGM中，tan∠AME=tan∠BMG，即

∠AME=∠BMG,

故

∠OMA=∠OMB.

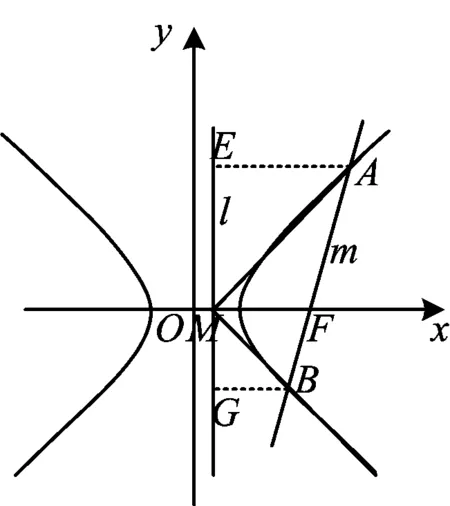
图6

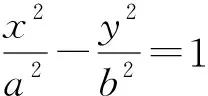
证明如图6，过点A作AE⊥l于点E，过点B作BG⊥l于点G.根据平行线分线段成比例，得

从而在Rt△AEM与Rt△BGM中,

tan∠AME=tan∠BMG,

即

∠AME=∠BMG，

故

∠FMA=∠FMB.

4 总结

波利亚对探索解题思路的过程建议分两步：第一，努力在已知和未知之间找出直接的联系；第二，如果找不出直接的联系，就对原来的问题做出某些必要的变更或修改，引进辅助问题[2].在解决问题时，必须对已经给出的有效条件进行分析，进而深入挖掘内含信息，内含信息的构建往往是解决问题的关键所在.

在本题中要使∠OMA=∠OMB得到证明，必须找出与两个角相等相关的内含信息：斜率、正切值、椭圆第二定义、角平分线的性质等，从这几个角度切入均可证∠OMA=∠OMB.通过5个角度的分析，从证法5中得到启示：在双曲线和抛物线中，如果满足在椭圆中的条件，则也满足求证的结论∠OMA=∠OMB.因此将该启示拓展到双曲线和抛物线中并证明，以期为学生和教师提供解决圆锥曲线的途径和方法.